
- •Производная функции, ее геометрический смысл.
- •Производная суммы, произведения и частного.
- •3.Производная сложной функции. Производная обратной функции
- •Дифференциал функции
- •Геометрический смысл дифференциала
- •Связь дифференциала с производной
- •2. Дифференциал суммы, произведения и частного.
- •4. Функции, заданные параметрически, их дифференцирование.
- •1. Производные высших порядков Понятие производных высших порядков
- •Формула Лейбница
- •4. Правило Лопиталя раскрытия неопределенностей
1. Производные высших порядков Понятие производных высших порядков
Пусть
функция![]() дифференцируема в некотором интервале.
Тогда её производная
дифференцируема в некотором интервале.
Тогда её производная
![]() ,
вообще говоря, зависит отх
, то есть
является функцией от х.
Следовательно, по отношению к ней снова
можно ставить вопрос о существовании
производной.
,
вообще говоря, зависит отх
, то есть
является функцией от х.
Следовательно, по отношению к ней снова
можно ставить вопрос о существовании
производной.
Определение.
Производная
от первой производной называется
производной
второго порядка или второй производной
и обозначается символом
![]() или
или![]() ,
то есть
,
то есть
![]() .
.
Пример
1. Найти
вторую производную от функции
![]() .
.
Решение. Найдем первую производную функции:
![]() .
.
Находим вторую производную как производную первой производной:
![]() .
.
Определение.
Производная
от второй производной называется
производной третьего порядка или третьей
производной и обозначается символом
![]() или
или![]() .
.
Определение.
Производной
n-ого
порядка функции
![]() называется
первая производная от производной
(n-1)-го
порядка данной функции и обозначается
символом
называется
первая производная от производной
(n-1)-го
порядка данной функции и обозначается
символом
![]() или
или![]() :
:
![]() .
.
Определение. Производные порядка выше первого называются высшими производными.
Пример
2. Найти
производную четвертого порядка функции
![]() .
.
Решение. Находим последовательно первую, вторую, третью и четвертую производные:
![]() ,
,
![]() ,
,![]() ,
,![]() .
.
Пример
3.Найти
производную n-ого
порядка для функции
![]() (k-const).
(k-const).
Решение. Имеем:
![]() ,
,
![]() ,
,![]() ,
,![]() .
.
Пример
4. Найти
производную n-ого
порядка для функции
![]() .
.
Решение. Имеем:
![]()
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
![]() Замечание.
Аналогично можно получить формулу n-ой
производной функции
Замечание.
Аналогично можно получить формулу n-ой
производной функции
![]() :
:
![]()
![]() .
.
![]() Пример
5. Найти
производную n-ого
порядка для степенной функции
Пример
5. Найти
производную n-ого
порядка для степенной функции
![]() , где
, где![]() и
и![]() - любое вещественное число.
- любое вещественное число.
![]() Решение.
Дифференцируя последовательно, получим:
Решение.
Дифференцируя последовательно, получим:
![]()
![]() ,
,
![]() ,
,![]()
![]() ,
,
![]()
![]() .
.
![]() В
частном случае, когда
В
частном случае, когда
![]() ,
гдеm
– натуральное число, получим:
,
гдеm
– натуральное число, получим:
![]()
![]() ,
,
![]() при
при![]() .
.
![]() Замечание.
При строгом выводе формулы для производной
n-ого
порядка следует применять метод
математической индукции.
Замечание.
При строгом выводе формулы для производной
n-ого
порядка следует применять метод
математической индукции.
![]()
![]() Вторая
производная параметрически заданной
функции
Вторая
производная параметрически заданной
функции
Если
функция задана параметрически уравнениями
![]() ,
то для нахождения производной второго
порядка нужно продифференцировать
выражение для её первой производной,
как сложной функции независимой
переменной.
,
то для нахождения производной второго
порядка нужно продифференцировать
выражение для её первой производной,
как сложной функции независимой
переменной.
Так
как
![]() ,
то
,
то
![]() ,
,
и с учетом того, что
![]() ,
,
получим
![]() ,
то есть
,
то есть
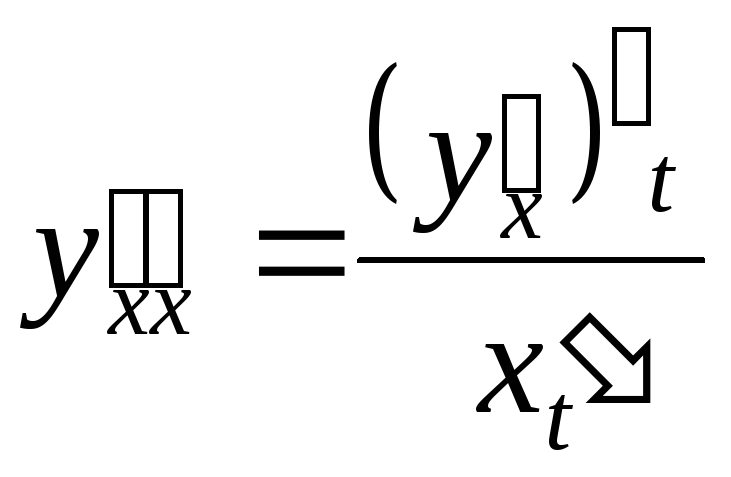 .
.
Аналогично можно найти третью производную
![]()
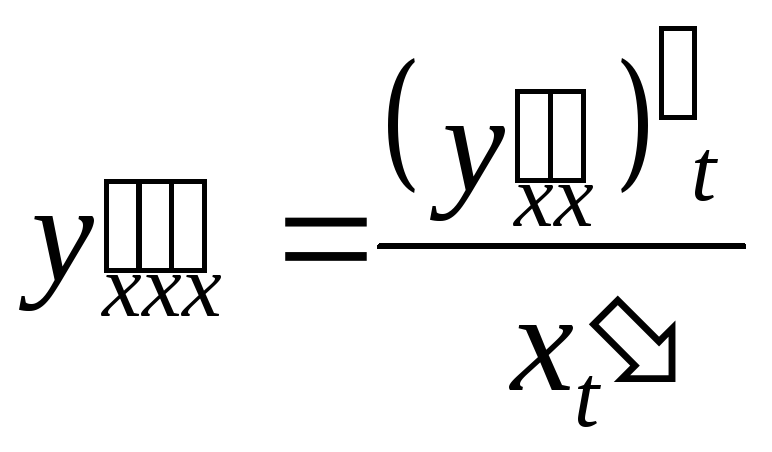 .
.
Пример
7. Найти
вторую производную параметрически
заданной функции
![]()
![]() ,
,![]() .
.
Решение.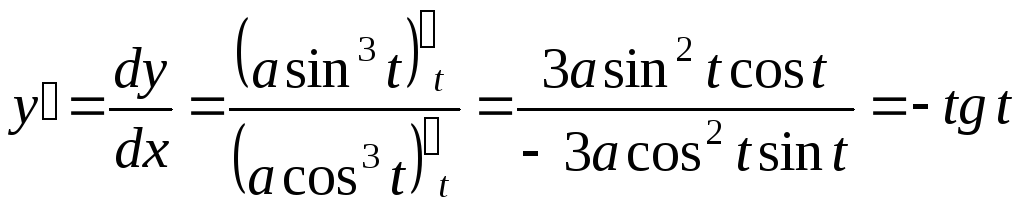 ,
,
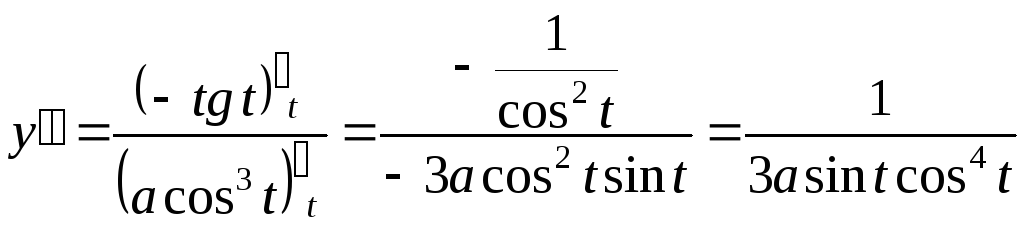 .
.
Формула Лейбница
Для нахождения производной n-ого порядка от произведения двух функций большое практическое значение имеет формула Лейбница.
Пусть
u
и
v
- некоторые
функции от переменной х,
имеющие производные любого порядка и
y=uv.
Выразим n-ую
производную
![]() через производные функцийu
и
v.
через производные функцийu
и
v.
Имеем последовательно
![]() ,
,
![]() ,
,
![]() .
.
Легко подметить аналогию между выражениями для второй и третьей производных и разложением бинома Ньютона соответственно во второй и третьей степенях, но вместо показателей степени стоят числа, определяющие порядок производной, а сами функции можно рассматривать как «производные нулевого порядка». Учитывая это, получим формулу Лейбница:
![]()
![]() . (2)
. (2)
Эту формулу можно доказать методом математической индукции.
Пример.
Найти пятую
производную функции
![]() .
.
Решение.
Положим
![]() и
и![]() .
Найдем
.
Найдем![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() .
Подставляя эти выражения в формулу
Лейбница при
.
Подставляя эти выражения в формулу
Лейбница при![]() ,
получим
,
получим
![]()
![]() .
.
