Задание 10

Найти частные производные второго порядка функции .

Частной производной по от функцииназывается предел; аналогично,

где и- соответственные частные приращения.

При вычислении частных производных используют следующее правило: частная производная по отравна производной от, вычисленной в предположении, что толькоявляется переменной, аформально считается постоянной. Аналогично вычисляется и частная производная по.

Пример. Дана функция . Найдем производные первого порядкаи. Считаяпостоянной, получим .

Считая постоянной, вычислим.

Подобным образом найдем производные второго порядка:

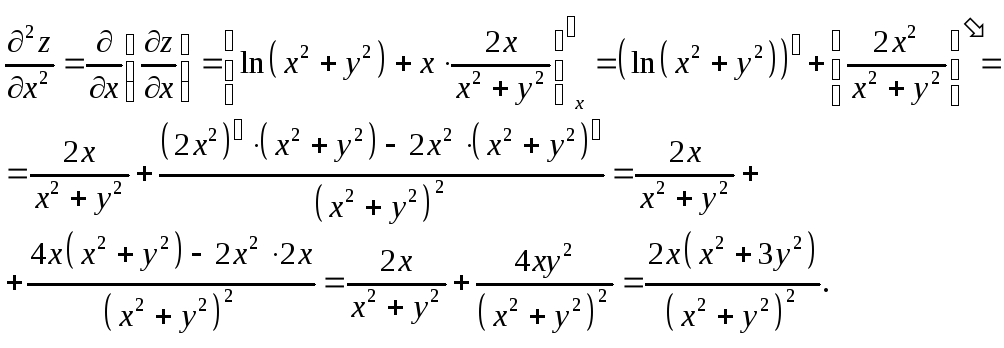
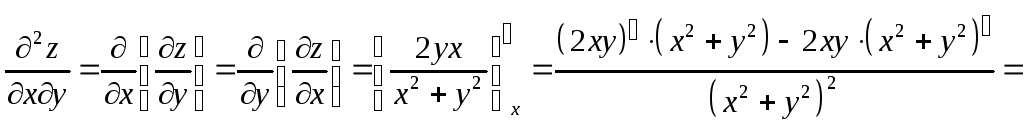
Задание 11

Пусть задана функция трех переменных . В трехмерном пространствесуществуют точки, в которых функцияпринимает одинаковое значение, которое обозначим через:

. (29)

С геометрической точки зрения (29) – уравнение некоторой поверхности, которую принято называть поверхностью уровня. Если величину изменять, то из (29) будем иметь семейство поверхностей уровня. Пусть функцияоднозначная. Тогда две различные поверхности уровня не будут пересекаться. Поверхности уровня обладают и еще одним свойством, для чего надо ввести понятие вектора – градиента:

. (30)

Оказывается, вектор , вычисленный в точке поверхности уровня, всегда направлен по нормали к этой поверхности.

Вектор удобно использовать при вычислении производной от некоторой функциипо заданному направлению вдоль единичного вектора, где.

Формула для вычисления производной по заданному направлению имеет вид скалярного произведения единичного вектора на вектор, вычисленного в некоторой точке, координаты которой должны быть заданы:

. (31)

Пример. Вычислить производную функции в точкепо направлению вектора.

Пусть (32)

Возьмем

.

а) Найдем координаты вектора в точкеМ. Для этого:

1) Запишем конкретный вид для :

.

2) Вычислим частные производные

; ;.

3) В точке они принимают значения

; ;.

Поэтому вектор в данной точкеимеет вид

. (33)

б) Найдем единичный вектор , имеющей направление.

1) Вектор имеет координаты

2) Длина вектора определяется по формуле .

3) Единичный вектор вдоль векторанайдем поформуле .

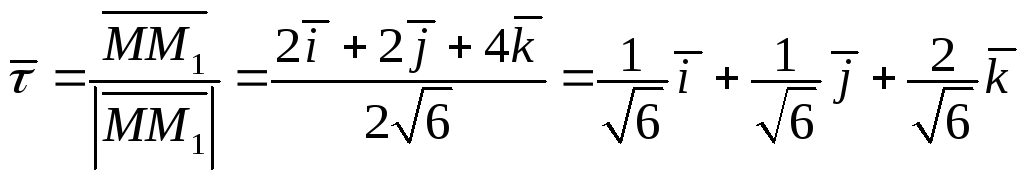Откуда . (34)

После подстановки вектора из (33) и значенийm, n, p из (34) в формулу (31) получим значение для искомой производной по заданному направлению

.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. М., Наука, 1984 (Дрофа, 2006)

2. Бутузов В.Ф., Крутицкая Н.Ч., Медведев Г.Н., Шишкин А.А. Линейная алгебра в вопросах и задачах. М., Наука, Физматлит, 2001.

3. Воеводин В.В. Линейная алгебра. М., Наука, 1980 (Лань, 2008)

4. Бутузов В.Ф., Крутицкая Н.Ч., Медведев Г.Н., Шишкин А.А. Математический анализ в вопросах и задачах. М., Наука, Физматлит, 2000.

5. Ильин В.А., Позняк Э.Г. Аналитическая геометрия: Учебник для вузов. М. Физматлит, 2007.

6. Ильин В.А., Позняк Э.Г. Линейная алгебра: Учебник для вузов. М. Физматлит, 2007.

7. Краснов М.Л., Киселев А.И., Макаренко Г.И. Шикин Е.В., Заляпин В.И. Вся высшая математика: Учебник. Т.1 – Т.6. Издательство УРСС, 2002.

8. Кудрявцев Л.Д. Краткий курс математического анализа. т. 1, 2. Альфа, 1998 (Физматлит, 2005).

9. Шипачев В.С. Высшая математика. М. Высш. школа. 2002.

10. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.1.: М. Высш. школа. 1996.

Учебное издание