
Формулы алгебры высказываний. Эквивалентность и преобразование формул
Напомним определение формулы алгебры высказываний. Формулами алгебры высказываний являются:
1) логические константы 0 и 1;
2) пропозициональные переменные;
3) если А и В – формулы, то каждое из выражений (А), (А) (В), (А) (В), (А) (В), (А) ~ (В) есть формула;
4) других формул, кроме построенных по пп. 1) - 3), нет.
Для проверки свойств эквивалентности, выполнимости, опровержимости, тождественной истинности и ложности формул могут использоваться таблицы истинности. Для построения таблицы истинности формулы воспользуемся следующим алгоритмом.
1. Пронумеровать простые высказывания в алфавитном порядке.
2. Для каждого элементарного высказывания рассмотреть все возможные наборы значений истинности. Всего возможно 2n комбинаций, где n - число элементарных высказываний. Это количество строк в таблице.
3. Пронумеровать сложные высказывания, содержащие одну логическую операцию, затем сложные высказывания, содержащие две логических операции, и т.д., увеличивая сложность высказываний в соответствии с порядком выполнения операций.
4. Вычислить значения истинности всех сложных высказываний. Столбец с последним номером будет содержать значение истинности для всей логической формулы.
Задание. Построить таблицу истинности формулы
(А В) А С.
Решение.
1. Пронумеруем простые высказывания в алфавитном порядке А-1, В-2, С-3.
2. Каждый набор значений истинности элементарных высказываний изобразится набором 000, 001, 010 и т. д. Для нашего примера число комбинаций равно 8-ми, то есть таблица истинности будет содержать 8 строк.
3. Пронумеруем сложные высказывания формулы: АВ - 4; ( - 5; - 6; С - 7; конечная операция - 8.
4. Вычислим последовательно значения истинности сложных высказываний.
|
( B |
|
С | ||||||
|
5 |
1 |
4 |
2 |
8 |
6 |
1 |
7 |
3 |
|
0 0 1 1 1 1 1 1 |
1 1 1 1 0 0 0 0 |
1 1 0 0 0 0 0 0 |
1 1 0 0 1 1 0 0 |
1 1 1 0 1 1 1 1 |
0 0 0 0 1 1 1 1 |
1 1 1 1 0 0 0 0 |
1 0 1 0 1 1 1 1 |
1 0 1 0 1 0 1 0 |
Анализируя истинностные значения формулы, содержащиеся в столбце 8, получим, что данная формула является и выполнимой, и опровержимой, и, следовательно, не тавтология и не противоречие. Для проверки эквивалентности формул строятся их таблицы истинности на одинаковых интерпретациях.
Однако такой способ очень громоздок, поэтому в дальнейшем для решения таких задач будем использовать эквивалентные преобразования, используя основные тавтологии 1-13.
Задание. Доказать эквивалентность формул (задание 3(а))
![]() .
.
Решение.
![]()
![]()
Формула 3(b) доказывается аналогично. В дальнейшем при проведении преобразований формул эти законы, называемые законами обобщенного склеивания, будут часто использоваться, поэтому добавим их под номером 14 в список основных тавтологий.
Задание. Доказать эквивалентность формул (задание 4(d))
(A B) (B C) (C A) (A B) (B C) (C A).
Решение.
(A B) (B C) (C A) (B (A C)) (C A)
(B (C A)) (A C (C A)) (B C) (B A) (A C).
Как легко видеть, последняя формула цепочки эквивалентна формуле правой части задания в силу коммутативности операций и . Данные формулы являются самодвойственными.
Для того чтобы воспользоваться тавтологиями 1-14 требуется привести формулу к приведенному виду. Определим порядок построения приведенной формулы.
Удаляются операции импликация и эквиваленция по формулам 11, 12.
Операции отрицания спускаются до высказывательных переменных с помощью законов де Моргана и двойного отрицания.
В дальнейшем, если это возможно, полученная приведенная формула упрощается с помощью свойств 3, 4, 5, 6, 9, 10.
Задание. Доказать тождественную истинность формулы (задание 6(а)) (P R) ((Q R) ((P Q) R)).
Решение.
(P R) ((Q R) ((P Q) R))
(![]() )
((
)
((![]() )
((P
Q)
R)
)
((P
Q)
R)
(![]() )
(
)
(![]() )
(
)
(![]() )
R
R
P
(
)
R
R
P
(![]() )
(
)
(![]() )
R
P
Q
(
)
R
P
Q
(![]() )
R
P
Q
)
R
P
Q
![]()
R
Q
1
1.
R
Q
1
1.
Начиная с 3-й, все формулы цепочки преобразований являются приведёнными.
Задание. Упростить схему
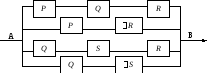
Решение. Запишем формулу, соответствующую схеме, по приведенным выше правилам
U
=
![]() .
.
