
- •2.1 Примеры и постановки задач оценивания постоянных параметров при обработке навигационной информации.
- •2.1.1 Оценивание коэффициентов полинома.
- •2.1.3 Постановка линейной задачи оценивания.
- •2.1.4 Определение временного запаздывания реализаций.
- •2.1.6 Определение координат и скорости по спутниковым данным.
- •2.1.7 Постановка нелинейной задачи оценивания и ее линеаризация.
- •2.1.8 Задача комплексной обработки избыточных измерений.
- •2.2 Алгоритмы оценивания на основе минимизации наблюдаемых критериев. Метод наименьших квадратов.
- •2.2.1 Основные положения и постановка задачи метода наименьших квадратов.
- •2.2.3 Точность оценивания метода наименьших квадратов.
- •2.3 Оптимальные в среднеквадратическом смысле линейные алгоритмы оценивания.
- •2.3.1 Постановка задачи получения оптимальных линейных оценок.
- •2.3.5 Задачи к разделу 2.3.
- •2.3.6 Вопросы к разделу 2.3.
- •2.4 Небайесовский метод оценивания.
- •2.4.1 Основные положения и постановка задачи.
- •2.4.6 Задачи к разделу 2.4.
- •2.4.7 Вопросы к разделу 2.4.
- •2.5. Байесовский метод оценивания.
- •2.5.1.Основные положения и постановка задачи.
- •2.5.2 Свойства оптимальных оценок.
- •2.5.3 Решение нелинейной гауссовской задачи.
- •2.5.8 Вопросы к разделу 2.5.
- •2.6.3 Централизованная и децентрализованная схемы обработки.
- •2.6.7 Задачи к разделу 2.6.
- •2.6.8 Вопросы к разделу 2.6.

2.2.3 Точность оценивания метода наименьших квадратов.
Достоинство рассмотренных методов заключается в том, что на этапе синтеза алгоритмов какая-либо априорная информация статистического характера не привлекается. Однако, как уже отмечалось выше, это затрудняет решение задачи анализа точности. Такая возможность открывается, если ввести предположение о случайном характере как ошибок измерения (в случае МНК и ОМНК), так и оцениваемого вектора (в случае ММНК). Обсудим более подробно эту возможность.
Будем считать, что ошибки измерения vi , i =1.m являются центрированными случайными величинами, для которых определена матрица ковариаций R . В этом случае, используя соотношения (1.5.2.), (1.5.3), легко убедиться в том, что ошибки оценок для МНК и ОМНК также будут центрированными с матрицами ковариаций, определяемыми как
Pмнк = M (K мнкv)(K мнкv)т |
|
= (H тH )−1 H тRH (H тH )−1 |
, |
(2.2.23) |
|
|
|
|
|
Pомнк = (H тQH )−1 H тQRQH (H тQH )−1 . |
|
(2.2.24) |
||
Для того, чтобы вычислить матрицу ковариаций ошибок оценивания для ММНК, необходимо задать статистические свойства не только для векторов v и x по отдельности, но, кроме того,
следует определить их взаимные статистические свойства. Если, к примеру, считать, что x и v некоррелированные между собой случайные векторы с математическими ожиданиями x и v = 0 и
матрицами ковариаций R , P x соответственно, то с использованием представления (2.2.22) в этом случае для матрицы ковариаций ошибок оценок ММНК можем получить следующее выражение
Pммнк = (E − K ммнкH )P x (E − K ммнкH )т +
(2.2.25)
+ K ммнкR(K ммнк )т ,
где матрица K ммнк задается выражением (2.2.12).
Если в критерии (2.2.11) принять Q = R−1 , то оценки ОМНК и матрица ковариаций их ошибок
могут быть записаны как
xˆ омнк ( y) = (H T R−1H )−1 H тR−1 y, |
|
|
|
|
|
|
|
|
|
(2.2.26) |
|||||||||
Pомнк = (H тR−1H )−1 . |
|
|
|
|
|
|
|
|
|
|
|
|
(2.2.27) |
||||||
Если, кроме того, считать, что |
D = (P |
x −1 |
, то |
K |
ммнк |
|
(P |
x |
−1 |
+ H |
т |
R |
−1 |
|
−1 |
т |
R |
−1 |
и |
) |
|
= |
|
) |
|
|
H |
H |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выражение для оценки (2.2.15) и соответствующей ей матрице ковариаций (см. задачу 2.2.3) примут следующий вид
xˆ ммнк ( y) = x + ((P x )−1 + H тR−1H )−1 H тR−1 ( y − Hx), |
(2.2.28) |
30

P |
ммнк |
|
(P |
x |
−1 |
+ H |
т |
R |
−1 |
|
−1 |
(2.2.29) |
|
= |
|
) |
|
|
H |
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Возможность вычисления матриц ковариаций ошибок оценивания обеспечивает существенное продвижение в решении задачи анализа точности, поскольку удается охарактеризовать ее на количественном уровне. В частности, диагональные элементы полученных матриц ковариаций ошибок оценивания (2.2.23)-(2.2.25) представляют собой дисперсии ошибок оценивания компонент искомого вектора x . Значения диагональных элементов матрицы P x обычно называют априорными дисперсиями ошибки оценивания. Такое название вполне обосновано, если считать, что до проведения измерений в качестве априорной оценки целесообразно использовать значение математического ожидания x . Сопоставление априорных дисперсий с соответствующими апостериорными дисперсиями (диагональными элементами матриц ковариаций (2.2.23)-(2.2.25)), т.е. теми, которые получены после проведения измерений с использованием различных алгоритмов, позволяет оценить эффективность этих алгоритмов.
Соответственно матрицу ковариаций P x называют априорной матрицей, а матрицы (2.2.23)- (2.2.25) - апостериорными матрицами ковариаций ошибок оценивания.
Если дополнительно наряду с предположением об известных значениях математических ожиданий и матриц ковариаций, считать, что ошибки измерения и оцениваемый вектор гауссовские, то в силу линейного характера преобразований (2.2.19)-(2.2.21), это обеспечивает гауссовский характер и ошибок оценивания для рассматриваемых методов. Иными словами, становится известной ф.п.р.в. для вектора ошибок оценивания. Наличие ф.п.р.в. обеспечивает полное описание их статистических свойств. В частности, для них могут быть рассчитаны такие рассмотренные в главе1 характеристики, как вероятная ошибка, предельная ошибка, квантили и т.д.
В качестве иллюстрации получим выражения для матриц ковариаций ошибок оценивания для рассмотренного в 2.1.5 примера задачи определения координат объекта на плоскости по измерениям дальностей до точечных ориентиров (2.1.16), полагая, что допустимо линеаризованное представление (2.1.29) и считая, что x ≡ δx = (x − x л ) - центрированный вектор с матрицей ковариаций P x , а ошибки измерения vi - некоррелированные между собой и с вектором
x центрированные с.в. с заданными дисперсиями ri2 , i =1.m . Принимая во внимание вид матрицы (2.1.32), нетрудно конкретизировать выражения для оценок (2.2.8), (2.2.26), (2.2.28) (см. задачу 2.2.6), соответствующих различным вариантам МНК. Матрицы ковариаций ошибок этих оценок будут определяться как
|
мнк |
|
л |
|
m |
л |
|
−1 |
m |
|
л |
m |
л |
−1 |
|
P |
(x |
) = |
|
|
|
2 |
M i (x |
|
|
,(2.2.30) |
|||||
|
|
∑M i (x |
|
) |
|
∑ri |
|
) ∑M i (x |
|
) |
|||||
|
|
|
|
|
i=1 |
|
|
i=1 |
|
|
i=1 |
|
|
|
|
31
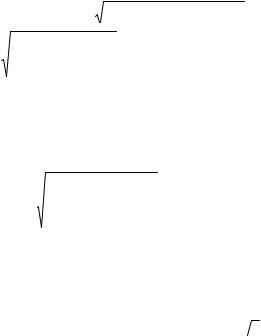
|
омнк |
|
|
|
л |
|
|
|
m |
1 |
|
|
|
|
|
|
л |
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
P |
|
|
|
|
(x |
|
) = ∑ |
|
M i (x |
|
) |
|
, |
|
|
|
|
|
|
|
|
|
(2.2.31) |
|||||||||||||
|
|
|
|
|
r 2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
i=1 |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ммнк |
|
|
|
л |
|
|
|
|
x |
|
−1 |
|
m |
|
|
1 |
|
л |
|
|
−1 |
|
|
|
|
||||||||||
P |
(x |
) |
= |
|
(P |
) |
+ |
∑ |
|
M i (x |
) |
|
, |
|
(2.2.32) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
r 2 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
(x |
л |
|
|
∆ |
sin 2 П |
i |
(x л) |
|
|
|
0.5sin 2П |
i |
|
(x л) |
(2.2.33) |
|||||||||||||||||||
i |
|
) = |
|
|
|
|
|
|
|
(x л) |
|
|
|
cos2 П |
|
|
|
|
|
|
. |
|||||||||||||||
|
|
|
|
|
|
|
|
0.5sin 2П |
i |
|
|
|
i |
(x л) |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Если считать измерения равноточными, |
т.е. |
полагать |
|
|
r |
2 = r 2 |
|
, |
|
|
i = |
|
, |
то приведенные |
||||||||||||||||||||||
|
|
|
|
|
1.m |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
выражения упрощаются к виду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мнк |
|
|
|
л |
|
|
|
|
омнк |
|
|
|
|
л |
|
|
|
2 |
|
m |
|
|
|
л |
|
−1 |
|
|
|
|
|||||
P |
(x |
) |
= P |
(x |
) = r |
|
∑M i (x |
|
|
|
, |
|
(2.2.34) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
−1 |
|
|
|
|
Pммнк |
(x л) |
= |
|
(P x )−1 + |
1 |
|
∑M i (x л) |
|
|
|
|
|
||||||||||||||||||||||||
|
|
. |
(2.2.35) |
|||||||||||||||||||||||||||||||||
r 2 |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Из представленных соотношений следует, что точность оценивания в рассматриваемой задаче в значительной степени определяется взаимным расположением точечных ориентиров. Действительно, вводя с использованием (1.3.24) радиальную среднеквадратическую погрешность определения координат места σместа , можем записать
σместа ≡ DRMS = |
Pомнк (1,1) + Pомнк (2,2) = |
m |
(2.2.36) |
= r Sp(∑M i (x л ))−1 . |
|
i=1 |
|
Отсюда следует, что σместа при одинаковой |
величине r в пренебрежении априорной |
информации определяется произведением среднеквадратической ошибки измерения дальностей на некоторый коэффициент
|
m |
л |
|
−1 |
|
PDOP = |
|
) |
|
, |
|
Sp ∑M i (x |
|
|
|||
|
i=1 |
|
|
|
|
зависящий от взаимного расположения точечных ориентиров. Этот коэффициент получил наименование геометрического фактора. В англоязычной литературе для него используется выражение Position Dilution of Precision. К примеру, в частном случае двух точечных ориентиров,
в условиях, когда П2 = П1 + 900 , нетрудно убедиться в том, что σместа ≡  2r (см. задачу 2.2.6). Очевидно, что при увеличении числа используемых ориентиров m , радиальная среднеквадратическая погрешность будет уменьшаться.
2r (см. задачу 2.2.6). Очевидно, что при увеличении числа используемых ориентиров m , радиальная среднеквадратическая погрешность будет уменьшаться.
В завершении этого раздела заметим, что в Matlab предусмотрена специальная процедура, 32
которая может быть полезной при решении задач с помощью метода МНК или ОМНК - X=LSCOV(H,y, Q−1 ). Эта процедура вырабатывает оценку (2.2.10), соответствующую решению задачи оценивания (2.1.10), (2.1.11) на основе минимизации критерия (2.2.9), причем в качестве входных данных выступают матрицы H и Q−1 . Размерность m × n матрицы H должна быть такой, чтобы m > n .
2.2.4 Сопоставление различных алгоритмов метода наименьших квадратов.
Применительно к линейной задаче проведем сопоставление алгоритмов, соответствующих различным вариантам МНК. Для того, чтобы провести их сравнение по точности, опираясь на соответствующие им матрицы ковариаций ошибок оценивания, будем полагать, что известны математическое ожидания оцениваемого вектора, соответствующая ему матрица ковариаций P x , а вектор ошибок не коррелирован с x и является центрированным вектором с матрицей ковариаций R . Кроме того, считаем, что в критерии ОМНК Q = R−1 , а в ММНК в качестве x
принято математическое ожидание вектора x и D = (P x )−1 .
При обсуждении взаимосвязи оценок, соответствующих различным вариантам МНК, целесообразно воспользоваться соотношением (2.1.15), которое с учетом сделанных предположений может быть переписано в виде
xˆ ммнк ( y) = Pммнк ((P x )−1 x + (Pомнк )−1 xˆ омнк ( y)). |
(2.2.37) |
Принимая во внимание соотношение (2.2.29) замечаем, что оценки и соответствующие им матрицы ковариаций ошибок для ОМНК и ММНК будут практически совпадать между собой,
если выполнено неравенство (P x )−1 << H тR−1H . Если, кроме того, полагать R = r 2 E , то оценки и
их ошибки для всех трех методов будут также практически одинаковыми.
Из выражения (2.2.37) следует, что оценка ММНК в рассматриваемой линейной задаче может быть сформирована в результате взвешивания x , определяющего априорное значение вектора x ,
и оценки xˆ омнк ( y) , полученной без учета этой априорной информации. Причем весовые матрицы,
стоящие перед x и xˆ омнк ( y) , совпадают с матрицами, обратными матрицам, характеризующим,
по сути, точность взвешиваемых величин. Ясно, что такая процедура возможна в случае, когда матрицы Pомнк и P x не вырождены. Очевидно, что при невырожденности матрицы Pммнк
допустима и обратная операция, предполагающая вычисление xˆ омнк ( y) по известному значению оценки ОМНК
xˆ омнк ( y) = Pомнк ((Pммнк )−1 xˆ ммнк − (P x )−1 x). |
(2.2.38) |
Возможность вычисления матриц ковариаций для различных алгоритмов, позволяет провести их сравнение по точности. При сделанных предположениях (Q = R−1 , D = (Px )−1) можно
33
показать (см., к примеру, задачу 2.2.5), что будет справедлива следующая цепочка неравенств
Pмнк ≥ Pомнк ≥ Pммнк. |
(2.2.39) |
Проведем более подробное обсуждение взаимосвязи различных алгоритмов на примере рассмотренной в разделе 2.1 задачи комплексной обработки данных от двух измерителей,
представленных в виде (2.1.33). При этом будем полагать, что v1 , v2 − некоррелированные между
собой центрированные векторы с известными матрицами ковариаций R j > 0, |
j =1,2 , |
а x - |
||
независящий от этих ошибок случайный вектор с математическим ожиданием |
x и матрицей |
|||
ковариаций P x , а в критерии ОМНК Q = R−1 . |
|
|
||
Принимая во внимание сделанные предположения и тот факт, что в этой задаче |
En×n |
|||
H = |
, где |
|||
|
|
|
En×n |
|
En×n - |
n × n , а матрица ковариаций для составного вектора ошибок измерений определяется как |
|||
R |
0 |
|
|
|
R = |
1 |
, можно, воспользовавшись полученными выше выражениями для оценок и матриц |
||
|
0 |
R2 |
|
|
ковариаций, соответствующих различным методам, конкретизировать их для рассматриваемой задачи. В результате для МНК и ОМНК получим
xˆ |
мнк |
= |
1 |
|
( y |
1 |
+ y |
2 |
), |
|
|
(2.2.40) |
|||
|
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Pмнк = |
|
1 |
(R |
+ R |
2 |
), |
|
|
(2.2.41) |
||||||
|
|
|
|
||||||||||||
|
|
|
2 |
|
1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
xˆ омнк = (R−1 |
+ R−1 ) |
−1 (R−1 y1 |
+ R−1 y 2 ), |
(2.2.42) |
|||||||||||
|
|
|
|
|
|
1 |
|
|
2 |
|
|
1 |
2 |
|
|
(2.2.43)
Из представленных соотношений следует, что при решении задачи комплексной обработки в случае МНК алгоритм сводится к простому осреднению имеющихся измерений, а в ОМНК эти измерения взвешиваются с весами, которые позволяют учесть различный уровень погрешностей используемых измерителей. Именно это обстоятельство и объясняет неравенство Pмнк ≥ Pомнк - в ОМНК предусмотрена возможность учета разного уровня погрешностей используемых измерений, в то время как в МНК все измерения выступают как равноправные.
Для ММНК искомые соотношения могут быть записаны как
xˆ ммнк ( y) = Pммнк ((P x )−1 x + (Pомнк )−1 xˆ омнк ( y)), |
(2.2.44) |
Pммнк = ((P x )−1 + R1−1 + R2−1 )−1. |
(2.2.45) |
Нетрудно заметить, что точно такие же соотношения могут быть получены, если вместо задачи оценивания x по измерениям (2.1.33) с использованием ОМНК, рассматривать задачу оценивания того же вектора с использованием ОМНК, но при этом к набору измерений (2.1.33) добавить
измерение вида |
|
y3 ≡ x = x + v3 , |
(2.2.46) |
34

в котором предполагается, что v3 - центрированный, некоррелированный с v1 и v2 случайный
вектор с матрицей ковариаций P x . Отсюда следует, что наличие априорной информации о векторе оцениваемых параметров может быть передано введением дополнительного измерения
(2.2.46).
Такая интерпретация позволяет дать простое объяснение неравенства Pмнк ≥ Pомнк , поскольку очевидно, что при увеличении числа используемых измерений точность может только повыситься. Отсюда следует, что ММНК, обладая отмеченным выше преимуществом перед МНК, обусловленным учетом разноточного характера измерений, приобретает еще одно достоинство – в нем предусмотрено привлечение дополнительного измерения, передающего факт наличия априорной информации, которая в ОМНК не используется.
Смысл сказанного о целесообразности учета имеющейся информации можно наглядно проиллюстрировать для частного случае рассматриваемой задачи, полагая, что оцениванию
подлежит скалярная величина с дисперсией |
σ |
2 |
, |
а дисперсии ошибок измерения равны r 2 |
и r 2 . |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
Приведенные соотношения преобразуются к виду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
xˆ мнк = |
( y |
+ y |
2 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
Pмнк |
|
|
r 2 |
+ r 2 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
1 |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
= |
1 |
|
|
2 |
|
|
, |
|
|
|
(2.2.47) |
||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
xˆ омнк = |
|
|
|
r 2 |
|
|
|
|
|
|
|
|
|
r |
2 |
|
|
|
|
Pомнк = |
|
r 2 r |
2 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
2 |
|
|
|
|
|
y |
+ |
|
|
|
1 |
|
y |
|
, |
|
1 |
2 |
|
|
|
, |
|
|
|
(2.2.48) |
||||||||||||
|
r 2 |
+ r |
|
|
|
r 2 |
+ r 2 |
|
|
r |
|
+ r |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
2 |
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
||||||||
|
ммнк = |
|
|
|
|
|
σ |
2 |
|
|
|
|
|
|
|
|
|
|
|
r 2 |
|
|
|
|
|
|
|
|
r 2 |
|
|
|
|
|
|
|
|
|
|
|||
xˆ |
|
|
|
|
|
|
0 |
|
|
|
|
|
x + |
|
|
|
2 |
|
|
|
y + |
|
|
|
|
|
1 |
|
|
|
|
|
|
y |
|
, (2.2.49) |
||||||
σ2 |
+ r |
|
|
+ r 2 |
σ |
2 + r 2 |
+ r 2 |
|
|
σ2 + r 2 |
+ r |
|
|
|||||||||||||||||||||||||||||
|
|
2 |
|
|
|
1 |
|
2 |
|
2 |
|
|
||||||||||||||||||||||||||||||
|
|
|
0 |
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
0 |
1 |
|
2 |
|
|
0 |
|
|
1 |
|
|
|
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
1 |
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pммнк = |
|
|
|
|
+ |
|
|
|
|
+ |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.2.50) |
||||||
|
|
|
|
r 2 |
|
r 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
σ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из выражений (2.2.48) следует, что, оценка, соответствующая ОМНК, действительно, формируется в результате суммирования измерений датчиков с весами, зависящими от их точности: чем точнее датчик, тем с большим весом войдет соответствующее измерение. Так, если r12 > r22 (второй датчик точнее), то весовой коэффициент для более точного измерения от второго датчика (измерение с меньшей дисперсией) больше, чем для более грубого измерения с большей дисперсией. Из (2.2.48) также следует, что в результате совместной обработки данных от двух измерителей с помощью ОМНК результирующая дисперсия ошибки оценивания Pомнк будет всегда меньше дисперсии любого из используемых по отдельности измерителей, т.е.
Pомнк = min(r12 , r22 ) . Применительно к ММНК аналогичное соотношение может быть записано как Pммнк = min(σ02 , r12 , r22 ) . Наибольший эффект достигается, когда σ02 = r12 = r22 , в этом случае величина среднеквадратической ошибки оценивания уменьшается в  2 раз для ОМНК и
2 раз для ОМНК и  3 раз – для ММНК. Понятно также, что в случае, когда одно из измерений существенно более точное, чем
3 раз – для ММНК. Понятно также, что в случае, когда одно из измерений существенно более точное, чем
35

остальные, например |
r 2 |
<< r 2 |
и |
r 2 |
<< σ2 |
, то в этом случае |
xˆîìíê ≈ xˆ ììíê |
≈ y , а |
|
|
|
1 |
2 |
|
1 |
0 |
|
|
1 |
Pомнк ≈ Pммнк ≈ r 2 |
. Это означает, |
что в |
качестве оценки фактически |
принимается |
наиболее |
||||
1 |
|
|
|
|
|
|
|
|
|
точное измерение и эффект от совместной обработки незначителен.
В завершении раздела о сопоставлении алгоритмов важно еще раз обратить внимание на тот факт, что все приведенные результаты будут справедливы лишь при выполнении отмеченных в начале раздела предположений о свойствах оцениваемого вектора и ошибок измерений, а кроме того, в критерии ОМНК Q = R−1 , а в ММНК в качестве x принято математическое ожидание
вектора x и D = (P x )−1 . При невыполнении этих условий при вычислении матриц ковариаций,
соответствующих ОМНК и ММНК, вместо (2.2.27), (2.2.29) необходимо использовать выражения (2.2.23), (2.2.24). Это повлечет не только изменение самих значений матриц ковариаций, но и может привести к нарушению соотношения между ними, задаваемого неравенством (2.2.39).
2.2.5 Задачи к разделу 2.2 |
|
Задача 2.2.1. Задан критерий вида |
|
J ммнк (x) = ( y − Hx)т R−1 ( y − Hx) + (x − x)т (P x )−1 (x − x) . |
(1) |
Покажите, что значение x , при котором этот критерий достигает минимального значения, определяется как
xˆ( y) = x + ((P x )−1 + H тR−1H )−1 H тR−1 ( y − Hx).
Примечание. Задачу решите, используя: а) систему нормальных уравнений; а) процедуру выделения полного квадрата.
Решение - вариант а).
Привлекая выражение (П1.30), систему нормальных уравнения можно записать как dJdx(x) = 2(H тR −1 ( y − Hx) + (P x )−1 (x − x))= 0 .
Отсюда следует, что
(H тR−1H + (P x )−1 )x = (P x )−1 x + H тR−1 y ,
или
(H тR−1H + (P x )−1 )x = (P x )−1 x + H тR−1Hx − H тR−1Hx + H тR−1 y.
Таким образом, значение аргумента, обеспечивающего минимум представленного критерия, будет определяться как
xˆ( y) = x + ((P x )−1 + H тR−1H )−1 H тR−1 ( y − Hx).
Решение - вариант б).Раскрывая скобки в (1), можем записать
36

J (x) = xт((Px )−1 + H тR−1H )x − 2xт(H тR−1 y + (Px )−1 x)+ x т(Px )−1 x + yтR−1 y .
Далее, используя |
выражение (П1.31), |
в |
котором в |
качестве |
A и |
z |
примем |
A = (P x )−1 + H тR−1H , |
z = H тR−1 y + (P x )−1 x , получаем |
|
|
|
|
||
|
J (x) = x т Ax − 2x т z + x т Ax + y тR−1 y = |
|
|
|
|||
|
= (x − A−1z)A(x − A−1z) − z т A−1z + +x т Ax + y тR −1 y. |
|
|||||
Поскольку три последних слагаемых от |
x |
не зависят, |
нетрудно |
понять, |
что |
значение |
|
аргумента, обеспечивающего минимум представленного критерия, будет определяться как |
|||||||
|
xˆ( y) = ((P x )−1 + H тR−1H )−1 (H тR−1 y + (P x )−1 x). |
|
|
||||
Учитывая, что (P x )−1 x ≡ ((P x )−1 + H тR−1H − H тR−1H )x , |
это выражение |
может быть |
|||||
преобразовано к виду |
|
|
|
|
|
|
|
|
xˆ( y) = x + ((P x )−1 + H тR−1H )−1 H тR−1 ( y − Hx). |
|
|
||||
Задача 2.2.2. Покажите, что для оценок, полученных МНК и ОМНК по измерениям (2.1.2) справедливы следующие соотношения [2.7, с. 412; 2.15, с. 101]
( y − yˆ мнк )т yˆ мнк = 0,
( y − yˆ омнк )т Qyˆ омнк = 0,
где yˆ мнк = HK мнк y, yˆ мнк = HK мнк y.
Решение.
Действительно, принимая во внимание (2.2.8), получим
(y − HK мнк y)т HK мнк y = y тHK мнк y − y т (K мнк )т H тHK мнк y =
= y т H (H тH )−1 H т − H (H тH )−1 H тH (H тH )−1 H т ) y = 0 .
Для ОМНК с учетом (2.2.10) аналогично
(y − HK омнк y)т QHK омнк y = y т QH (H тQH )−1 H тQ − QH (H тQH )−1 H тQ y = 0 .
Задача 2.2.3. Пусть в критерии (2.2.11) Q = R−1 , D = (P x )−1 , и, таким образом в выражении для оценки xˆммнк( y) = x + K ммнк( y − Hx) , соответствующей ММНК, матрица K ммнк определяется как
K ммнк = ((P x )−1 + H тR−1H )−1 H тR−1 . Полагая, что x и v - некоррелированные случайные
векторы, с матрицами ковариаций P x и |
R , |
а математическое ожидание вектора |
|||||||
покажите, что матрица ковариаций ошибок оценок ММНК определяется как |
|||||||||
P |
ммнк |
|
(P |
x −1 |
+ H |
т |
R |
−1 |
−1 |
|
= |
) |
|
|
H . |
||||
|
|
|
|
|
|
|
|
|
|
x равно x ,
(1)
37
Решение.
Подставляя K ммнк в выражение (2.4.4) и принимая во внимание, что
E − K ммнкH = E − ((P x )−1 + H тR −1H )−1 (H тR −1H + (P x )−1 − (P x )−1 ) = = ((P x )−1 + H тR−1H )−1 (P x )−1,
можем записать
P |
ммнк |
|
|
(P |
x |
|
−1 |
+ |
H |
т |
R |
−1 |
H |
−1 |
(P |
x |
|
−1 |
(P |
x |
−1 |
+ H |
т |
R |
−1 |
H |
|
−1 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
= |
|
|
) |
|
|
|
|
|
|
|
|
) |
|
|
) |
|
|
|
|
|
|
+ |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(P |
x |
−1 |
+ H |
т |
R |
−1 |
H |
|
−1 |
H |
т |
R |
−1 |
|
(P |
x |
|
−1 |
+ H |
т |
R |
−1 |
H |
|
−1 |
= |
|
|
|
|
|||||||||||||||||||||||
+ |
|
|
) |
|
|
|
|
|
|
|
|
|
H |
) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
(P |
x |
|
−1 |
+ H |
т |
R |
−1 |
|
−1 |
|
|
x |
−1 |
+ H |
т |
R |
−1 |
|
|
|
(P |
x |
−1 |
+ |
H |
т |
R |
−1 |
|
−1 |
|||||||||||||||||||||||
= |
|
|
) |
|
|
|
|
H |
(P |
|
|
) |
|
|
|
H |
|
) |
|
|
|
|
H |
, |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
откуда с очевидностью следует (1).
Задача 2.2.4. Получите выражения для дисперсии ошибок оценивания, соответствующих трем вариантам МНК применительно к задаче оценивания скалярной величины по измерениям (2.1.1),
считая x - случайной величиной с математическим ожиданием x и дисперсией σ02 , а ошибки измерения центрированными, некоррелированными между собой и с x случайными величинами с
дисперсиями r 2 , i = |
|
. Упростите полученные выражения, полагая дополнительно, что r 2 = r 2 , |
|||||||||||||||||||||||||||||
1.m |
|||||||||||||||||||||||||||||||
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
||||||
т.е. дисперсии одинаковы для всех i = |
|
|
. В критерии ММНК примите |
|
d =1/ σ02 . |
При каких |
|||||||||||||||||||||||||
1.m |
|
||||||||||||||||||||||||||||||
условиях точность полученные оценок будет для различных методов совпадать? |
|
|
|
|
|
||||||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Поскольку при сделанных предположениях матрица R диагональная, то для МНК получим |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
∑r 2 |
|
|
|
|
|
|
|
|
|
r 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Pмнк = |
i=1 i |
, |
|
|
Pмнк |
= |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
m2 |
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
||||
Полагая матрицу Q также диагональной с элементами |
|
q |
i |
=1/ r 2 , в первом случае, и |
q |
i |
=1/ r 2 , |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|||
i = |
|
- во втором, для ОМНК и ОМНК будем иметь следующие выражения |
|
|
|
|
|
|
|
||||||||||||||||||||||
1.m |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
m |
1 |
−1 |
|
|
|
|
|
|
r2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Pомнк = |
∑ |
|
|
|
|
, |
|
|
|
|
Pомнк = |
|
|
, |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
i=1 |
|
|
ri |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
1 |
|
|
m |
1 |
−1 |
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
||||
|
|
|
|
Pммнк = |
|
+∑ |
|
, |
|
|
Pммнк = |
|
|
σ0r |
|
|
. |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
σ2 |
|
|
i=1 |
r 2 |
|
|
|
|
|
|
|
r 2 + σ |
2m |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
0 |
|
|
i |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
1 |
−1 |
||
В рассматриваемом примере оценки ОМНК и ММНК будут совпадать, когда σ02 >> |
|
∑ |
. |
||||||||||||||||||||||||||||
r 2 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
i |
|
|||
Это неравенство, в частности, справедливо, если априорная дисперсия существенно превышает дисперсию ошибок измерения.
38
Задача 2.2.5. Предположим, что имеется 2 m измерений в задаче оценивания постоянной величины по измерениям (2.1.1), которые можно разбить на две группы, причем в каждой из них различны значения дисперсий ошибок измерения: для первых m измерений эта дисперсия равна
r |
2 |
, а для вторых - |
r 2 . Кроме того, |
полагаем, что |
|
x - |
центрированная с.в. с дисперсией σ2 |
, а в |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|||
критерии |
(2.2.9) |
|
матрица |
|
Q |
|
|
|
- |
|
|
|
|
диагональная |
|
|
с |
|
|
|
элементами |
|
q |
|
|
|
=1/ r 2 |
,i = |
|
|
|
и |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
1.m |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
q |
|
=1/ r 2 ,i = |
|
|
|
, а в (2.2.11), кроме того, |
x = 0 и d =1/ |
σ2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
i |
(m +1).2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Получите выражения для оценок и дисперсий их ошибок, соответствующих различным |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
алгоритмам, и покажите, что неравенства (2.2.7) справедливы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Алгоритмы вычисления оценок для МНК, ОМНК и ММНК будут иметь следующий вид: |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xˆ мнк ( y) = |
|
|
|
|
|
∑yi , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r 2 |
|
|
|
|
1 |
m |
|
|
|
|
|
|
|
|
|
|
r 2 |
|
|
1 |
2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xˆ омнк ( y) = |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
∑yi |
+ |
|
|
|
1 |
|
|
|
|
|
∑yi , |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
2 |
|
+ r |
2 |
|
|
m |
r |
2 |
+ r |
2 |
|
m |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
i=m+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
xˆ ммнк ( y) = |
|
|
|
|
|
|
|
|
r 2 r |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ2 m(r 2 |
|
+ r |
2 ) |
|
|
|
|
xˆ омнк ( y) ≈ xˆ омнк ( y). |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
0 + |
|
|
|
|
|
0 |
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
r |
2 r |
|
|
|
|
|
|
|
|
|
|
|
+ r |
2 ) |
r |
2 r |
|
|
|
|
|
|
|
|
|
|
+ r 2 ) |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 + σ |
2 m(r 2 |
|
|
|
2 |
+ σ2 m(r 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
0 |
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Дисперсии ошибок определятся как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мнк |
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
омнк |
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
ммнк |
|
|
|
|
|
1 |
|
|
2 |
2 |
|
−1 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
= |
r1 |
+r2 |
|
|
|
, |
P |
= |
|
|
|
|
|
r1 |
r2 |
|
|
|
|
|
|
|
|
|
|
P |
= |
|
|
|
|
+ |
m(r1 |
+r2 ) |
. |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
2 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m(r1 |
+r2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ0 |
|
r1 |
r2 |
|
|
|||||||||||||||||||||
|
|
|
Поскольку σ02 > 0 , то легко убедиться в справедливости следующей цепочки неравенств |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pмнк ≥ Pомнк ≥ Pммнк, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
r 2r 2 |
|
|
|
r |
2 |
+ r |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
в случае, |
если |
|
|
|
1 |
2 |
|
≤ |
|
|
1 |
|
2 |
|
. |
|
|
|
Представив |
|
|
r |
|
|
|
как |
|
r |
= αr |
, |
|
|
можем |
записать |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(r12 + r22 ) |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
r |
2 |
+ r 2 |
r |
2r 2 |
= r 2 |
1 + α |
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
1 |
+ α |
|
|
|
α |
|
|
|
|
|
|
(1 + α)2 |
|
− 4α |
|
|
|
|
|
(1 − α)2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
1 |
2 |
− |
1 2 |
|
|
|
|
|
− |
|
|
|
|
|
|
|
≥ |
|
0 , |
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
≥ 0 , |
|
т.к. |
||||||||||||||||||||||
|
|
|
4 |
|
(r 2 |
+ r 2 ) |
2 |
|
4 |
|
|
|
|
1 + α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
1 + α |
|
|
|
|
|
|
1 + α |
|
|
|
|
|
|
|
|
|
1 + α |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α > 0 .
Задача 2.2.6. Применительно к задаче оценивания координат объекта на плоскости по измерениям (2.1.16) для случая двух точечных ориентиров конкретизируйте основанный на линеаризации алгоритм получения оценки и алгоритм вычисления соответствующей ей матрицы ковариаций для МНК. Рассчитайте величину геометрического фактора. При этом считайте, что выполнены следующие предположения: точка линеаризации расположена в начале координат;
один из точечных ориентиров расположен на оси ox2 ; второй – на оси ox1 ; ошибки измерения -
некоррелированные между собой центрированные случайные величины с одинаковыми дисперсиями, равными r 2 . При каких условиях полученные оценки совпадут с ОМНК и ММНК?
39
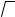
Решение. |
|
|
|
|
|
|
|
|
|
|
|
Вводя |
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
(x |
л |
) |
|
|
~ |
(x |
|
) |
H = |
|
|
|
|
y |
л |
|||||
|
1 |
(x |
|
|
|
и |
y = ~1 |
|
|
||
H |
2 |
л) |
|
y2 (xл) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
и используя (2.2.8), (2.2.23), получим
δxˆ |
мнк |
т |
т |
(xл )H 2 (xл )) |
−1 |
т |
~ |
т |
~ |
(xл )), |
|
= (H1 |
(xл )H1 (xл ) + H 2 |
|
(H1 |
(xл ) y1 |
(xл ) + H 2 |
(xл ) y2 |
Pмнк = r 2 (H1т (xл)H1(xл) + H 2т (xл)H 2 (xл))−1 ,
где H i (x л ) = (sin Пi (x л ), cos Пi (x л )), i =1,2 .
Принимая во внимание тот факт, что П1 (x л ) = 0 , а П2 (x л) = 90° , запишем
~ |
(x |
|
) |
|
y |
л |
, |
||
δxˆ мнк = ~1 |
|
|
||
y2 |
(xл ) |
|
||
r 2 |
0 |
|
|
Pмнк = |
0 |
r 2 |
. |
|
|
||
|
|
|
|
Величина геометрического фактора в данном случае будет равна PDOP =  2 .
2 .
Проводя необходимые преобразования с учетом введенных обозначений, получаем, что уточенные координаты объекта, вычисляемые с помощью МНК, будут определяться как
xˆiмнк = xiл + δxˆiмнк = xiл + yi − Di (xл ), i =1,2 .
Полученные оценки будут совпадать с оценками ОМНК, если весовая матрица Q выбрана
диагональной с элементами 1/ r 2 , а матрица D нулевая.
Задача 2.2.7. Получите алгоритм нахождения координат для случая двух точечных ориентиров при тех же предположениях, что и в предыдущей задаче, но при условии, что один точечный
ориентир расположен под углом П1 , а другой под углом П1 + 900 относительно оси ox2 .
Прокомментируйте полученный результат.
Задача 2.2.8. Используя ОМНК, решите задачу оценивания неизвестного n -мерного вектора x с использованием двух n -мерных измерений
y1 = v1 − v2 , y 2 = x + v2 ,
в которых v1 , v2 предполагаются некоррелированными между собой случайными центрированными векторами с матрицами ковариаций R1 > 0 , R2 > 0 .
Сопоставьте полученную оценку решение с оценкой (2.2.41), (2.2.42), соответствующей задаче
оценивания x по измерениям (2.1.33). |
|
|
|
|
||||
Решение |
|
|
|
|
|
|
|
|
Сформулированная |
задача |
легко сводится |
к |
задаче общего вида, |
если ввести матрицу |
|||
0 |
|
, вектор |
ошибок |
(v1 − v2 , |
т |
и |
соответствующую ему |
матрицу ковариаций |
H = |
n×n |
v2 ) |
||||||
En×n |
|
|
|
|
|
|
|
|
40

R |
+ R |
2 |
− R |
2 |
|
. Решая ее с использованием соотношений (2.2.26), (2.2.7) легко убедиться в |
|
R = |
1 |
|
|
|
|||
|
− R2 |
|
R2 |
|
|
||
том, что полученное решение совпадет с (2.2.41), (2.2.42). |
|
Задача 2.2.9. Пусть имеются измерения |
|
yi = hx + εi , |
(1) |
в которых ошибки εi представляются в виде |
|
εi = d + vi |
(2) |
суммы центрированной случайной величины с дисперсией σd2 |
и независимых между собой и |
от d центрированных случайных величин с одинаковыми дисперсиями ri2 = r 2 , i =1.m .
А. Полагая, что оцениванию подлежат значения x и d , запишите выражение для матрицы H
ипроверьте выполнение условия наблюдаемости.
B. Полагая, что оцениванию подлежат только значение скалярной величины x , получите выражения для оценок, соответствующих МНК и ОМНК, рассчитайте дисперсии их ошибок. Сопоставьте полученные выражения и поясните полученные результаты.
Решение. |
|
|
|
|
|
|
|
|
|
A. В случае, если оцениванию подлежат значения x и d , матрица H будет иметь вид |
|
||||||||
|
1 |
1 . |
. |
1 |
|
|
|
|
|
|
H т = h |
1 . |
. |
. |
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
||
Отсюда следует, что |
|
m |
m |
|
и, |
таким |
образом, |
условие |
|
матрица H тH = h2 |
|
- вырождена, |
|||||||
|
|
m |
m |
|
|
|
|
|
|
наблюдаемости не выполнено. |
|
|
|
|
|
|
|
|
|
B. В случае, если оцениванию подлежат |
только |
значение |
x , |
очевидно, что |
условие |
||||
наблюдаемости будет |
выполнено, поскольку |
матрица |
H т = h[1,1....1] , и, |
таким |
образом, |
||||
H тH = h2 m .
Выражения (2.2.8), (2.2.23) для оценки и дисперсии ее ошибки для МНК в этом случае будут иметь вид
|
1 |
m |
|
|
|
|
|
|
|
|
|
|
|
|
xˆ мнк ( y) = |
∑yi , |
|
|
|
|
|
|
|
|
|
|
|
(3) |
|
hm |
|
|
|
|
|
|
|
|
|
|
|
|||
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pмнк = (H тH )−1 H тRH (H тH )−1 = |
σd2 |
+ |
|
r 2 |
|
. |
(4) |
|||||||
h2 |
mh2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Учитывая результаты решения задачи 1.5.2, матрицу ковариаций ошибок для вектора |
ε и |
|||||||||||||
обратную ей матрицу можем представить в виде |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
||
R = r 2 E + σ2 |
I , R −1 = |
E − |
|
σd |
|
|
|
I |
, |
(5) |
||||
|
2 |
2 |
|
2 |
|
|||||||||
|
d |
|
r |
|
|
|
|
|
|
|
||||
|
|
|
|
|
mσd + r |
|
|
|
|
|
|
|||
41
где I - матрица, составленная из единичек. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Таким образом, используя (2.4.1), (2.4.19), (2.4.20), имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y1 |
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑yi |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
y2 |
|
|
|
|
|
σd |
|
1 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σd |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
. |
|
|
||||||||||||||
|
|
|
|
|
|
|
R |
|
y |
= |
|
|
|
E |
− |
|
|
|
|
|
|
|
|
|
|
I |
y = |
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|||||||||||
|
|
|
|
|
|
|
|
r |
2 |
|
|
|
2 |
|
|
|
|
2 |
|
r |
2 |
|
|
|
|
|
|
2 |
|
+ r |
2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mσd + r |
|
|
|
|
|
|
|
|
|
|
|
|
|
mσd |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ym |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
σ |
2 |
|
|
|
|
|
|
|
h m |
|
|
|
|
|
|
|
mσ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
m |
||||||||||
|
т |
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
R |
|
y = |
r |
2 |
|
E |
− |
|
|
|
2 |
|
+ r |
2 |
I y |
= |
|
r |
2 ∑y j 1 − |
|
|
2 |
|
|
|
|
2 |
= |
|
|
|
2 |
|
+ r |
2 ∑y j . |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
nσd |
|
|
|
|
|
|
|
|
|
j= |
|
|
|
|
mσd + r |
|
|
|
|
|
|
|
mσd |
|
|
j= |
||||||||||||||||||||
Принимая во внимание эти соотношения, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
xˆ омнк ( y) = (H тR −1H )−1 H тR −1 y = |
|
∑yi , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6) |
||||||||||||||||||||||||||||||||
|
|
|
|
|
hm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Pомнк = (H тR−1H )−1 = |
1 |
|
|
r |
2 |
|
2 |
+ r |
2 |
|
|
|
2 |
|
|
|
|
|
r |
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
mσd |
|
|
= |
|
σd |
|
+ |
|
|
|
|
. |
|
|
|
(7) |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
m |
r |
|
|
|
|
|
|
h |
2 |
|
|
|
|
mh |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Сопоставляя (3), (4) с (6), (7), отмечаем их совпадение. Ясно, что такое совпадение возможно только при совпадении минимизируемых критериев, которые в рассматриваемой задаче записываются как
J мнк |
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= ( y − Hx)т ( y − Hx) = ∑( yi − hx)2 , |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
омнк |
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
||
J |
|
= ( y − Hx)т R −1 ( y − Hx) |
= ( y − Hx)т |
E − |
σd |
|
|
|
I ( y − Hx) . |
|||||||||||
|
|
|
2 |
|
|
|
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
2 |
+ r |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mσd |
|
|
||||
Принимая во внимание вид матриц H и R−1 , получим |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
омнк |
1 |
|
|
|
σ2 |
|
|
m |
|
|
2 |
|
|
|
||||
|
|
m |
|
|
|
|
|
|
|
|
|
|||||||||
|
J |
|
|
|
∑( yi − hx) |
2 |
|
|
d |
|
|
|
∑( yi |
|
|
|
|
|
|
|
|
= |
r |
2 |
|
− 2 |
+ r |
2 |
|
|
− hx) |
|
. |
(8) |
|||||||
|
|
|
|
i=1 |
|
|
mσd |
|
|
i=1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приводя подобные слагаемые для записанного в скобках выражения, можно убедиться в том,
что с точки зрения минимизации критериев относительно x оно совпадает с J мнк .
Таким образом, замечаем, что оценки и минимизируемые критерии в данном частном случае
совпадают. Это факт есть следствие того, |
что в рассматриваемой задаче искомый параметр x и |
|||
постоянная составляющая ошибки d |
одновременно не наблюдаемы, т.е. они не могут быть |
|||
определены по отдельности. |
|
|
|
|
Этим же объясняется и тот факт, что |
|
|
|
|
омнк |
|
σ2 |
|
|
P |
≥ |
d |
, |
, |
|
||||
|
|
h2 |
|
|
т.е. дисперсия ошибки оценивания x при увеличении числа измерений, при котором
42
обеспечивается существенное снижение ( |
r 2 |
<< σd2 ) влияния составляющей ошибки vi , |
|
m2 |
|||
|
|
определяется дисперсией постоянной составляющей ошибки измерения.
2.2.6 Вопросы к разделу 2.2
1.Сформулируйте постановку задачу оценивания с использованием наблюдаемых критериев
ипоясните особенности МНК, ОМНК и ММК. Что такое невязка измерений и система нормальных уравнений? Приведите пример системы нормальных уравнений для задачи оценивания фазы.
2.Получите алгоритмы вычисления оценок МНК и его модификаций для линейной задачи. Проиллюстрируйте применение этих алгоритмов на примере решения простейшей задачи оценивания постоянной величины.
3.Приведите уравнения для ошибок оценок МНК и его модификаций и выражения для матриц ковариаций. Какие дополнительные предположения необходимо ввести для вычисления матриц ковариаций ошибок оценивания, получаемых с помощью МНК?
4.На примере задачи совместной обработки данных от двух измерителей проанализируйте особенности, взаимосвязь и отличия различных вариантов МНК.
43
