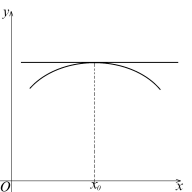
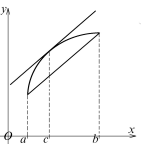
Производная обратной функции. Производная функции, заданной параметрически. Производная функции, заданной в неявном виде.
Производная обратной функции
Дифференцируемая монотонная функция f: ]a, b[ → R с необращающейся в нуль производной имеет обратную дифференцируемую функцию f -1, производная которой вычисляется по формуле
![]()
![]()
Производная параметрически заданной функции
Если функция f задана параметрически
x = φ(t), y = ψ(t), α < t < β,
где y = f(x) и функции φ и ψ дифференцируемы, причем φ'(t) ≠ 0, то
![]()
![]()
Производная неявно заданной функции
Если y = f(x) - дифференцируемая функция, заданная уравнением F(x, y) = 0, т. е. F(x, f(x)) ≡ 0 на некотором интервале ]a, b[, то во многих случаях ее производную можно найти из уравнения
![]()
![]()
Логарифмическая производная – производная от натурального логарифма модуля (абсолютной величины) – данной функции:
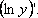
Используя формулу производной сложной функции, найдем, что
![]() (*)
(*)
Логарифмическую производную используют, например, при дифференцировании (нахождении производной или дифференциала) степенно-показательной функции.
Пример:
Найдём
производную функции у = хx.
Поскольку lny= xlnx,
легко найти логарифмическую производную:
![]()
Теперь
с помощью формулы (*) получим:
![]()
Таблица производных
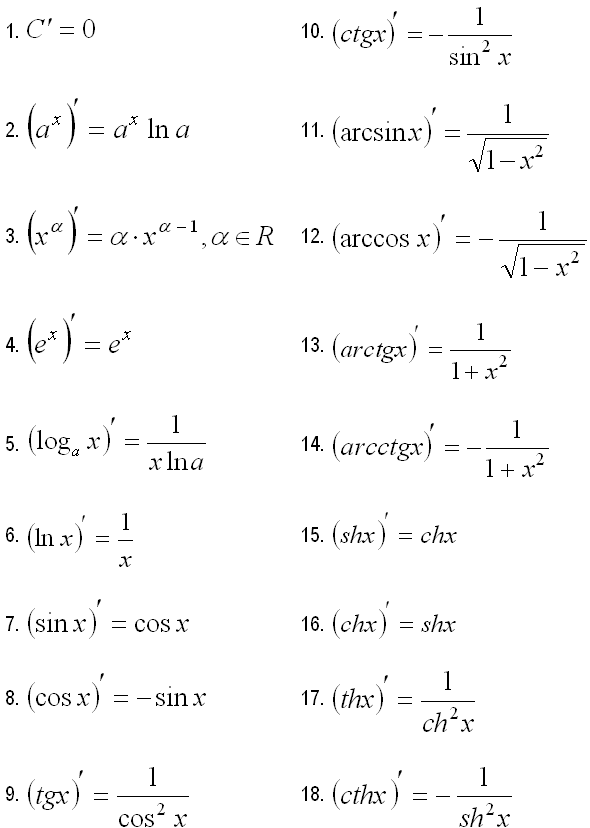 КРОМЕ
15-18!
КРОМЕ
15-18!
Теорема Ферма
Если
функция ![]() имеет
производную и в точке
имеет
производную и в точке ![]() имеет
экстремум, то значение производной в
этой точке равно 0.
имеет
экстремум, то значение производной в
этой точке равно 0.
Доказательство
Пусть ![]() -
точка минимума. Тогда при
-
точка минимума. Тогда при ![]() .
Значение выражения
.
Значение выражения  .
Значит,
.
Значит, 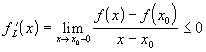 .
Рассмотрим теперь
.
Рассмотрим теперь ![]() ,
при этом также
,
при этом также ![]() ,
и выражение
,
и выражение 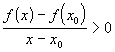 .
Значит, правая производная
.
Значит, правая производная 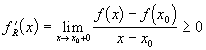 .
.
![]() .
Из ранее доказанного следует:
.
Из ранее доказанного следует: 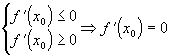 .
Теорема доказана.
.
Теорема доказана.
|
|
Геометрический смысл теоремы Ферма Существует
такая точка Замечания
|
Равность нулю производной - необходимое условие существования экстремума, но не достаточное. То есть производная может быть равной 0 и вне точки экстремума. Пример:
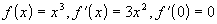 ,
но точка 0 - не экстремум.
,
но точка 0 - не экстремум.
Теорема Ролля
Пусть:
Функция
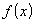 непрерывна
на отрезке
непрерывна
на отрезке  :
: 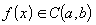 ;
;Для любого x из интервала
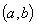 существует
производная:
существует
производная: 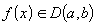 ;
;Значения функции на концах отрезка равны:
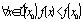 .
.
Тогда
существует такое ![]() ,
что производная
,
что производная ![]() .
.
Доказательство
Функция непрерывна
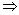 существуют
существуют  .
.Если
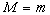 ,
то функция
,
то функция 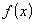 является
константой, и ее производная в любой
точке равна 0, т.е. теорема доказана.
является
константой, и ее производная в любой
точке равна 0, т.е. теорема доказана.Если же
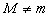 ,
то оба значения
,
то оба значения  не
могут достигаться в концевых точках,
т.к.
не
могут достигаться в концевых точках,
т.к. 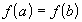 и
и 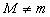 .
Тогда хотя бы одно из них достигается
во внутренней точке c,
и, по теореме Ферма 17.1
.
Тогда хотя бы одно из них достигается
во внутренней точке c,
и, по теореме Ферма 17.1 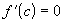
Замечания:
Существует хотя бы одна точка, в которой касательная к графику функции параллельна оси Ox (см. рисунок к теореме Ферма).
Все условия теоремы Ролля существенны, т.е. нельзя отбростиь хотя бы одно из них.
Первое следствие теоремы Ролля
Пусть:
Функция
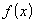 непрерывна
на отрезке
непрерывна
на отрезке 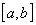 :
: 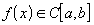 ;
;Функция дифференцируема на интервале
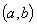 :
: 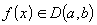 ;
;Сужествуют
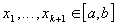 такие,
что
такие,
что 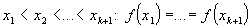 .
.
Тогда ![]() такие,
что
такие,
что ![]() .
.
Доказательство
Рассмотрим
отрезок ![]() .
Данный отрезок удовлетворяет всем
требованиям теоремы Ролля. Тогда
.
Данный отрезок удовлетворяет всем
требованиям теоремы Ролля. Тогда ![]() .
.
Применив теорему Ролля k раз, доказываем данное следствие.
Второе следствие теоремы Ролля
Пусть:
Существует функция, имеющая n производных, непрерывных на отрезке
 :
: 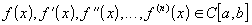 ;
;Для любого x из интервала
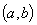 существует
n+1 производная:
существует
n+1 производная: 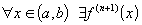 ;
;Значения
 .
.
Тогда
существует такая точка ![]() .
.
Доказательство
По теореме Ролля для
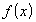 на
отрезке
на
отрезке 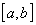
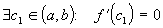 .
.Рассмотрим отрезок
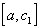 ,
на котором
,
на котором  непрерывна.
Тогда существует производная
непрерывна.
Тогда существует производная 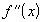 на
интервале
на
интервале  .
Так как
.
Так как 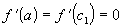 .
Значит, существует точка
.
Значит, существует точка 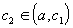 такая,
что
такая,
что 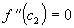 .
Рассмотрим отрезок
.
Рассмотрим отрезок 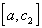 ,
на котором
,
на котором 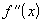 непрерывна.
Значит,
непрерывна.
Значит, 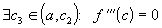 .
На n-ном
шаге имеем:
.
На n-ном
шаге имеем: 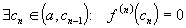 .
Рассмотрим
.
Рассмотрим 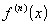 на
на 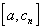 .
. Функция непрерывна на
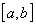 ,
значит, она непрерывна и на
,
значит, она непрерывна и на 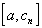 :
: 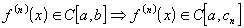 ;
;Для любого x из
 существует n+1
производная:
существует n+1
производная: 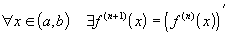 ;
;Значения ее на концах равны:
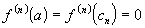 .
.
Данные
3 заключения удовлетворяют условию
теоремы Ролля. Значит, ![]() .
.
Теорема Лагранжа
Пусть:
Функция
 непрерывна
на отрезке
непрерывна
на отрезке 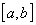 :
: 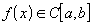 ;
;Функция дифференцируема на интервале
 :
: 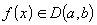
.
Тогда
существует такая точка ![]() ,
что
,
что ![]() .
.
Доказательство
Рассмотрим
вспомогательную функцию ![]() .
.
Эта функция непрерывна, т.к.
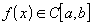 ,
, 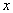 -
непрерывна.
-
непрерывна.Данная функция имеет производную
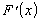 ,
так как для любого
,
так как для любого 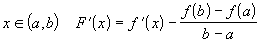 .
.Значения на концах равны:
 ,
, 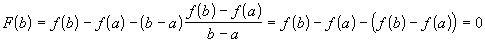 .
.
Эти
3 рассуждения удовлетворяют условию
теоремы Ролля, следовательно, ![]() .
Таким образом,
.
Таким образом, ![]() ,
, ![]() .
.
|
|
Геометрический смысл теоремы Лагранжа
|
Первое следствие теоремы Лагранжа.
(Критерий постоянства функции на промежутке).
Пусть
существует множество ![]() ,
и для всякого
,
и для всякого ![]() значение
производной равно 0. Тогда данная функция
является постоянной, т.е.
значение
производной равно 0. Тогда данная функция
является постоянной, т.е. ![]() .
.
Доказательство
![]() .
Очевидно, что
.
Очевидно, что ![]() .
.
![]() .
Достаточно доказать, что
.
Достаточно доказать, что ![]() .
Ранее доказано, что из дифференцируемости
функции в точке следует ее непрерывность.
Поэтому
.
Ранее доказано, что из дифференцируемости
функции в точке следует ее непрерывность.
Поэтому ![]() ,
и, в частности,
,
и, в частности, ![]() .
Так как
.
Так как ![]() и
и ![]() .
Значит, по теореме Лагранжа,
.
Значит, по теореме Лагранжа, ![]() такое,
что
такое,
что ![]() ,
т.к.
,
т.к. ![]() .
Следовательно,
.
Следовательно, ![]() .
.
Данное следствие часто называется основной леммой интегрального исчисления.
Замечание
Если X состоит из нескольких отрезков, то функция будет постоянной на каждом из этих отрезков, но эти постоянные могут быть не равны.
Второе следствие теоремы Лагранжа.
Если
для любого ![]() значение
производной больше 0, то эта функция
возрастает на интервале
значение
производной больше 0, то эта функция
возрастает на интервале ![]() .
(Если меньше 0 - убывает).
.
(Если меньше 0 - убывает).
Доказательство
Пусть
существуют ![]() такие,
что
такие,
что ![]() .
Функция
.
Функция ![]() непрерывна
на отрезке
непрерывна
на отрезке ![]() ,
так как она дифференцируема на
,
так как она дифференцируема на ![]() и
и ![]() .
Тогда
.
Тогда ![]() ,
т.е. дифференцируема и на
,
т.е. дифференцируема и на ![]() .
Значит, по теореме Лагранжа,
.
Значит, по теореме Лагранжа, ![]() .
Так как всегда
.
Так как всегда ![]() ,
то значение
,
то значение ![]() непосредственно
зависит от значения производной. То
есть знак функции совпадает со знаком
производной.
непосредственно
зависит от значения производной. То
есть знак функции совпадает со знаком
производной.
Третье следствие теоремы Лагранжа.
Пусть
X - некоторый промежуток, и значения
производной на этом промежутке ограничены
числом C: ![]() .
Тогда функция
.
Тогда функция ![]() равномерно
непрерывна на данном промежутке.
равномерно
непрерывна на данном промежутке.
Доказательство
Требуется
доказать, что ![]() (см.
определение равномерной непрерывности).
По теореме Лагранжа имеем:
(см.
определение равномерной непрерывности).
По теореме Лагранжа имеем: ![]() .
Обозначив
.
Обозначив ![]() ,
получаем:
,
получаем: ![]() .
.
Пример:
функция ![]() ,
имеющая ограниченную производную
,
имеющая ограниченную производную ![]() ,
,![]() .
Данная функция действительно является
равномерно непрерывной.
.
Данная функция действительно является
равномерно непрерывной.
Теорема Коши
Если функции f(x) и g(x) непрерывны на отрезке [a, b] и дифференцируемы на интервале (a, b) и g(x) 0 на интервале (a, b), то существует по крайней мере одна точка , a < < b, такая, что
![]() .
.
Т.е. отношение приращений функций на данном отрезке равно отношению производных в точке . Примеры решения задач курс лекций Вычисление объема тела по известным площадям его параллельных сечений Интегральное исчисление
Для доказательства этой теоремы на первый взгляд очень удобно воспользоваться теоремой Лагранжа. Записать формулу конечных разностей для каждой функции, а затем разделить их друг на друга. Однако, это представление ошибочно, т.к. точка для каждой из функции в общем случае различна. Конечно, в некоторых частных случаях эта точка интервала может оказаться одинаковой для обеих функций, но это- очень редкое совпадение, а не правило, поэтому не может быть использовано для доказательства теоремы.
Доказательство. Рассмотрим вспомогательную функцию
![]() ,
,
которая на интервале [a, b] удовлетворяет условиям теоремы Ролля. Легко видеть, что при х = а и х = b F(a) = F(b) = 0. Тогда по теореме Ролля существует такая точка ,
a < < b, такая, что F() = 0. Т.к.
![]() ,
то
,
то
![]()
А
т.к. ![]() ,
то
,
то ![]()