Тема 9. Законы распределения случайных величин

9.1.Случайная величина ξ имеетбиномиальное распределениес параметрамиnиp(n– натуральное число, 0p1), если она принимает значения 0, 1, … ,nс вероятностями

.

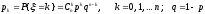Заметим, что характеристическое свойство (7.1) (см. тему 7) выполняется, так как в силу формулы бинома Ньютона

.

Биномиальное распределение является распределением числа “успехов” в nиспытаниях Бернулли с вероятностью “успеха”pи “неудачи”q= 1 –pв каждом испытании (см. тему 6).

Математическое ожидание и дисперсия с.в. ξ:

M=np,D=npq.

Максимум вероятностей p_k(k= 0, 1, … ,n) достигается приk= [np –q] + 1, которое называетсянаиболее вероятным(илинаивероятнейшим) числом “успехов” вnиспытаниях Бернулли. Здесь [x] – целое число отx.

9.2.Случайная величина ξ имеетгипергеометрическое распределениес параметрамиN,M,n(N,M,n– натуральные числа,M N,nN), если она принимает значенияm₀,m₀+ 1,m₀+ 2, … ,m₁, с вероятностями

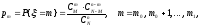
где

m₀ = max (0, N – M + n), m₁ = min (M, n).

Гипергеометрическое распределение является распределением числа объектов, обладающих заданным свойством среди nобъектов, случайным образом извлеченных (без возвращения) из совокупностиNобъектов, из которыхMобладают этим свойством (см. тему 2).

Математическое ожидание и дисперсия с.в. ξ:

.

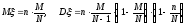9.3.Случайная величина ξ имеетгеометрическое распределениес параметромp(0 <p< 1), если она принимает значения 1, 2, … ,n, …. (счетное множество значений) с вероятностями

.

Воспользовавшись формулой суммы бесконечно убывающей геометрической прогрессии, убеждаемся, что характеристическое свойство (7.1) (см. тему 7) выполняется:

.

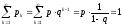Геометрическое распределение является распределением числа испытаний Бернулли до появления первого “успеха”, если вероятность “успеха” в каждом испытании равна p.

Математическое ожидание и дисперсия с.в. ξ:

.

9.4.Случайная величина ξ имеет распределение Пуассонас параметром(> 0), если она принимает значения 0, 1, … ,n, …. (счетное множество значений) с вероятностями

.

Характеристическое свойство (7.1) снова выполнено, так как

.

Распределение Пуассона является пределом биномиального распределения, когда в схеме Бернулли nиp0 так, чтоnp=> 0. Поскольку при этом вероятность “успеха”pмала, то распределение Пуассона часто называютзаконом распределения редких событий.

Математическое ожидание и дисперсия с.в. ξ совпадают:

M=D=.

9.5.Случайная величина ξ имеет равномерное распределениена отрезке [a,b], гдеa<b, если её плотность распределенияp(x) постоянна на этом отрезке и равна нулю вне его:

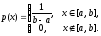
Функция распределения с.в. ξ, распределенной по равномерному закону на отрезке [a, b], имеет вид

Графики функций p(x) и F(x) приведены на рис. 9.1.

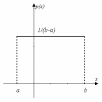
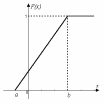
Рис.9.1. Плотность и функция распределения равномерного закона

Математическое ожидание и дисперсия равномерно распределенной с.в. ξ:

.

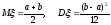9.6. Случайная величина ξ имеет показательное (илиэкспоненциальное)распределение с параметром(> 0), если её плотность распределенияp(x) имеет вид

Функция распределения с.в. ξ, распределенной по показательному закону, равна

Графики функций p(x) и F(x) приведены на рис. 9.2.

Рис.9.2. Плотность и функция распределения показательного закона

Математическое ожидание и дисперсия показательно распределенной с.в. ξ:

.

9.7.Случайная величина ξ имеет нормальное распределение с параметрамиaи(–<a<,> 0), если её плотность распределенияp(x) выражается формулой

,

а функция распределения

,

где

–функция Лапласа (см. тему 6).

Подчиненность с.в. нормальному закону распределения с параметрамиaисимволически обозначаетсяN(a,).

Графики функций p(x) иF(x) приведены на рис. 9.3.

Рис.9.3. Плотность и функция распределения нормального закона

Математическое ожидание с.в., распределенной по нормальному закону, равно параметру a, дисперсия равна²:

M=a,D=².

Нормальное распределение при a= 0 и= 1 называетсястандартным нормальным. Плотность и функция распределения этого закона распределения равны соответственно

и , –<x<.

Теорема.Пусть с.в.N(a,)и <х₁, х₂> один из интервалов (конечный или бесконечный) вида [х₁,х₂], [х₁,х₂), (х₁,х₂], (х₁,х₂). Тогда

1) ;

2) для любого числа> 0.

9.8.Измерение дальности до объекта сопровождается систематическими и случайными ошибками. Систематическая ошибка равна 50 м в сторону занижения дальности, а случайные ошибки подчиняются нормальному закону со средним квадратическим отклонением 0,1 км. Определить вероятность того, что

a) ошибка измерения не превзойдет по абсолютной величине 150 м;

b) измеренная дальность не превзойдет истинной.

Решение. Испытание – измерение дальности до объекта. Пусть A и B – события, описанные в п.п. a) и b) соответственно. Обозначим через  суммарную ошибку измерения дальности (в метрах). Её систематическая составляющая a = – 50 (м), а случайная составляющая  имеет нормальное распределение с M = 0 и () = 100 (м). Тогда суммарная ошибка

 = a + 

также подчиняется нормальному закону с математическим ожиданием (см. темы 7 и 8)

M = M(a + ) = M(a) + M() = a + 0 = – 50 (м),

дисперсией (см. также темы 7 и 8)

D = D(a + ) = D(a) + D() = 0 + (())² = 10 000 (м²)

и стандартным отклонением

(м).

a) Согласно формуле 1) теоремы п. 9.7 имеем

= Ф₀(2) – Ф₀(– 1) = Ф₀(2) + Ф₀(1) = 0,4772 + 0,3413 = 0,8185.

Здесь мы воспользовались нечетностью функции Лапласа Ф₀(x) и таблицей её значений.

b) Аналогично получаем

= Ф₀(0,5) – Ф₀(– ) = Ф₀(0,5) + Ф₀() = 0,1915 + 0,5 = 0,6915,

так как .

9.9. Из урны, содержащей 3 белых и 7 черных шаров, одновременно извлекаются 4 шара. Определить среднее значение, дисперсию и стандартное отклонение числа белых среди извлеченных шаров.

9.10. Из урны, содержащей 3 белых и 7 черных шаров, извлекаются шары по одному до тех пор, пока не появится черный шар. Определить среднее значение, дисперсию и стандартное отклонение числа вынутых белых шаров, если каждый шар после извлечения:

a) возвращается в урну; b) не возвращается в урну.

9.11. Вероятность отказа каждого прибора при испытании не зависит от отказов остальных приборов и равна 0,2. Испытано 10 приборов. Найти среднее значение, дисперсию и стандартное отклонение числа отказавших за время испытаний приборов.

9.12. Вероятность отказа каждого прибора при испытании не зависит от отказов остальных приборов и равна 0,2. Приборы испытываются до первого отказа. Найти среднее значение, дисперсию и стандартное отклонение:

a) числа испытанных приборов; b) числа приборов, выдержавших испытание.

9.13. Средняя плотность болезнетворных микробов в одном кубическом метре воздуха равна 100. Пусть случайная величина  – число болезнетворных микробов, находящихся в 2 дм³ воздуха, взятом на пробу. Найти закон распределения с.в. . Какова вероятность того, что в пробе будет обнаружен хотя бы один микроб?

9.14. Деталь, изготовленная станком-автоматом, считается годной, если отклонение её контролируемого размера от номинала не превышает 10 мм. Случайные отклонения контролируемого размера от номинала подчиняются нормальному закону с нулевым средним значением и стандартным отклонением 5 мм.

a) Каков в среднем процент годных деталей, производимых станком-автоматом?

b) Сколько необходимо изготовить деталей, чтобы с вероятностью не менее 0,95 среди них оказалась хотя бы одна бракованная деталь?

9.15.Ошибка показаний вольтметра складывается из систематической ошибки прибора, равной 0,5 В, и случайной ошибки измерений, имеющей нормальное распределение со средним 0,1 В и средним квадратическим отклонением 0,4 В. Определить вероятность того, что в результате четырех независимых измерений напряжения в цепи величина ошибок показаний не более двух раз превысит 0,8 В.

9.16. Усилие, растягивающее стержень, является случайным, подчиняющимся нормальному закону со средним значением 10 кг и дисперсией 250 000 гр². Усилие, разрушающее стержень, составляет 10,5 кг. Производится испытание 5 стержней. Найти вероятность того, что:

a) ни один из стержней не разрушится;

b) разрушится не более двух стержней;

c) хотя бы один из стержней разрушится.

9.17.Мост со сторонами 360 м и 24 м подвергается бомбардировке группой из четырех бомбардировщиков, летящих вдоль моста. Каждый самолет осуществляет прицеливание по центру моста и сбрасывает одну бомбу. Систематические отклонения точки попадания бомбы от точки прицеливания отсутствуют, но имеются случайные отклонения по длине и ширине моста, которые независимы и имеют нормальные распределения со стандартными отклонениями 450 м по длине и 30 м по ширине. Определить вероятность разрушения моста, если для этого достаточно попадания в мост одной бомбы.

1)¹⁾ В дальнейшем данную операцию будем называть описанием пространства элементарных исходов испытания.

46