Тема 4. Теоремы сложения и умножения вероятностей

Теоремы сложения вероятностей:

1. Если события АиВнесовместны, то.

2. Если события АиВсовместны, то.

3. Если события 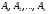попарно несовместны, то

.

4. Если события не являются попарно несовместными, то

.

Теоремы умножения вероятностей:

1. Если события АиВнезависимы, тоP(AB) =P(A)P(B).

2. Если события АиВзависимы, то.

3. Если события взаимно независимы (независимы в совокупности), то

.

4. Если события не являются взаимно независимыми, то

Пример 4.1. Для сигнализации об аварии в офисе некоторой фирмы установлены три сигнализатора различных типов, которые работают независимо друг от друга. Известно, что при аварии сигнализатор первого типа срабатывает в среднем в 95% всех аварий, второго типа – в 90%, третьего – в 80%. Найти вероятность того, что при аварии:

a) сработает только один сигнализатор;

b) сработают два сигнализатора;

c) сработают не менее двух сигнализаторов;

d) сработает хотя бы один сигнализатор;

e) все сигнализаторы поведут себя одинаково, т.е. либо сработают, либо нет.

Решение. Испытание ­– проверка функционирования трех сигнализаторов во время аварии. Пусть A, B, … , E – события, описанные в п.п. a), b), … , e) примера 4.1. Введем также следующие события:

A_i = {во время аварии сработает i–й сигнализатор}, i = 1, 2, 3.

По формулам классического определения вероятности и вероятности противоположного события находим

P(A₁) = 0,95, 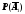= 1 –P(A₁) = 0,05; P(A₂) = 0,9, = 1 –P(A₂) = 0,1;

P(A₃) = 0,8, = 1 –P(A₃) = 0,2.

Кроме того, по условию события А₁, А₂, А₃ независимы.

a) Событие А произойдет, если произойдет какое-либо одно из следующих трех попарно несовместных событий:

сработает 1-й сигнализатор, а 2-й и 3-й не сработают – это событие ;

сработает 2-й сигнализатор, а 1-й и 3-й не сработают – это событие ;

сработает 3-й сигнализатор, а 1-й и 2-й не сработают – это событие .

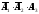Следовательно, событие А можно представить в виде суммы трех попарно несовместных событий: А = . Используя теорему сложения вероятностей для совокупности попарно несовместных событий и теорему умножения вероятностей для независимых событий, получим

=

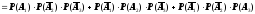= 0,95×0,1×0,2 + 0,05×0,9×0,2 + 0,05×0,1×0,8 = 0,032.

b) Событие В означает срабатывание любых двух сигнализаторов их трех, т.е.

.

Снова по теоремам сложения вероятностей для попарно несовместных событий и умножения вероятностей для независимых событий, имеем

_{……………………………………………}………………………………………………………………………………………….= 0,283.

c) Очевидно, событие С наступит, если сработают любые два сигнализатора из трех (событие В) или сработают все три сигнализатора (событие F = A₁× A₂× A₃), т.е. C = B + F. Тогда, снова используя теоремы сложения вероятностей для попарно несовместных событий и умножения вероятностей для независимых событий, получим

Р(С) = Р(B + F) = Р(B) + Р(F) = …………………………………………… = 0,967.

d) Событие D представляет сумму несовместных событий А (включающего три варианта) и С (четыре варианта), т.е. D = А + С (семь вариантов). По теореме сложения вероятностей для двух событий находим

Р(D) = Р(А + С) = Р(А) + Р(С) = 0,032 + 0,967 = 0,999.

Можно проще найти вероятность события D, если перейти к противоположному событию, включающему всего один вариант: . Применяя формулу для вероятности противоположного события и теорему умножения вероятностей для независимых событий, получим

=

= 1 – 0,05×0,1×0,2 = 1– 0,001 = 0,999.

Таким образом, срабатывание во время аварии хотя бы одного сигнализатора является практически достоверным событием.

e)

Пример 4.2.Два игрока подбрасывают монету по три раза каждый. Определить вероятность того, что:

a) у игроков будет одинаковое число гербов;

b) уIигрока будет больше гербов, чем уII;

c) уIIигрока будет больше гербов, чем уI.

Решение.Испытание – подбрасывание монеты по три раза каждым. ПустьA,B,C– события, описанные в п.п.a),b),c) примера 4.2.

Первый способ(использование классического определения вероятности). Рассматриваемое испытание эквивалентно, очевидно, подбрасыванию монеты 6 раз. Поскольку при каждом подбрасывании монета может выпасть двумя способами, то в силу правила умножения (см. тему 2) всего исходов испытанияN= 2⁶= 64. Используя правила сложения и умножения можно подсчитать количество исходов испытания, благоприятствующих событиямA,BиC:N(A),N(B) и N(C).

Второй способ(применение теорем сложения и умножения вероятностей).

Введем следующие события: A^I_i= {уIигрока выпадетiгербов},A^II_i= {уIIигрока выпадетiгербов},i= 0, 1, 2, 3. Тогда событиеAможно тогда представить в следующем виде:

A = A^I₀  A^II₀ + A^I₁  A^II₁ + A^I₂  A^II₂ + A^I₃  A^II₃ ,

где слагаемые являются попарно несовместными, а сомножители – независимыми событиями. Применяя теорему сложения вероятностей для попарно несовместных событий и теорему умножения вероятностей для независимых событий, получаем

P(A) = P(A^I₀)P(A^II₀) + P(A^I₁)P(A^II₁) + P(A^I₂)P(A^II₂) + P(A^I₃)P(A^II₃).

Вычисление отдельных вероятностей в последнем выражении опять же можно произвести двумя способами: непосредственным (используя классическое определение вероятности при 3-х кратном подбрасывании монеты) и с помощью теорем сложения и умножения вероятностей.

Пример 4.3. На стеллаже библиотеки в случайном порядке расставлено 15 учебников, причем 5 из них в твердом переплете, а остальные – в мягком. Библиотекарь берет наудачу три учебника. Найти вероятность того, что из взятых учебников:

a) только один будет в твердом переплете;

b) два будут в твердом переплете;

c) не менее двух будут в твердом переплете;

d) хотя бы один будет в твердом переплете;

e) все будут в одинаковых переплетах .

Решение. Испытание – из 15 книг наудачу берутся 3 книг (без возвращения и без учета порядка следования книг среди отобранных). Следовательно, число всевозможных исходов данного испытания равно числу сочетаний из 15 по 3:

.

Обозначим через A, B, … , E – события, описанные в п.п. a), b), c), … , e) примера 4.2. Определим также следующие события:

A_i = {среди отобранных 3 книг i книг в твердом переплете}, i = 0, 1, 2, 3.

Найдем вероятности событий A_i (i = 0, 1, 2, 3) по формуле гипергеометрических вероятностей при n = 15 (все учебники на стеллаже), n₁ = 5 (книги в твердом переплете на стеллаже), k = 3 (взятые книги со стеллажа) и k₁ = i = 0, 1, 2, 3 (книги в твердом переплете среди взятых):

, i = 0, 1, 2, 3.

Отсюда

……………= …………… = 0,494;

……………= …………… = 0,220;

P(A₃) = ……… = ………………= …………… = 0,022.

а) Очевидно, интересующее нас событие А = А₁, поэтому P(A) = P(A₁) = 0,494.

b) Аналогично, событие B = А₂, поэтому P(B) = P(A₂) = 0,2240.

c) Событие C произойдет, если два учебника будут в переплете (это событие А₂) или три учебника будут в переплете (это событие А₃). Следовательно, событие C можно представить в виде суммы двух несовместных событий: C = А₂ + А₃. Тогда по теореме сложения вероятностей для двух несовместных событий имеем

Р(C) = ………………………………………………………. = 0,242.

d) Первый способ. Событие D произойдет, если произойдет любое из следующих трех несовместных событий:

будет один учебник в твердом переплете – это событие А₁;

будут два учебника в твердом переплете – это событие А₂;

будет три учебника в твердом переплете – это событие А₃.

Следовательно, событие D можно представить в виде суммы трех попарно несовместных событий: D = A₁ + А₂ + А₃. Тогда по теореме сложения вероятностей для совокупности попарно несовместных событий имеем

Р(D) = Р(A₁ + А₂ + А₃) = Р(A₁) + Р(А₂) + Р(А₃) = 0,494 + 0,220 + 0,022 = 0,736.

Второй способ. События D и А₀ являются противоположными, т.е. А₀ =, поэтомуР(D) = 1 – = 1 –Р(А₀) = 1 – 0,264 = 0,736.

e)

Пример 4.4. В коробке имеется 12 электролампочек, среди которых 4 бракованные, неотличимые по виду от доброкачественных. Некто наугад берет электролампочку, ввинчивает ее в патрон и включает ток. Бракованная лампочка сразу же перегорает; она выбрасывается и проверяется следующая. И так до тех пор, пока не будет гореть лампочка. Найти вероятность того, что будет выброшено не более двух электролампочек.

Решение.Испытание состоит в том, что поочередно (и без повторения) проверяются электролампочки до тех пор, пока не будет обнаружена доброкачественная. Пусть событиеАзаключается в том, что будет выброшено не более двух электролампочек, т.е. количество выброшенных лампочек равно 0, 1 или 2. Это событие, очевидно, эквивалентно тому, что будет удачной первая, вторая или третья попытка замены лампочки. Обозначим черезсобытие, состоящее в том, что i-я лампочка доброкачественная,i = 1, 2, 3. Тогда событиеАможно представить в виде

,

где слагаемые являются попарно несовместными событиями. Применяя вначале теорему сложения вероятностей для несовместных событий, а затем теорему умножения вероятностей для зависимых событий, находим

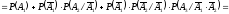
g

Пример 4.5.Имеется коробка с девятью новыми теннисными мячами. Для игры берут наугад три мяча, и после игры их кладут обратно. Какова вероятность того, что после трех игр в коробке не останется неигранных мячей? Предполагается, что при выборе мячей игранные от неигранных не отличаются.

Решение. Испытание – выбор трех мячей из девяти для трех игр, т.е. три раза, с возвращением мячей обратно в коробку. Пусть событиеАсостоит в том, что после трех игр все мячи в коробке будут игранными.

Первый способ(классическое определение вероятности).

Первое действие – выбор для 1-й игры 3 мячей (без возвращения и без учета порядка) из 9 мячей в коробке – может быть осуществлено способами; 2-е действие – выбор для 2-й игры 3 мячей (без возвращения и учета порядка) из 9 мячей – может быть осуществленоспособами; наконец, 3-е действие – выбор для 3-й игры 3 мячей (без возвращения и учета порядка) из 9 мячей – может быть осуществлено такжеспособами. Согласно правилу умножения число всевозможных исходов рассматриваемого испытания равно

.

Аналогичным образом находим N(A) = ……………………… и

.

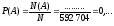Второй способ(теоремы сложения и умножения вероятностей).

Событие Аможно представить в виде произведения трехзависимыхсобытий:А=А₁ А₂ А₃, где событиеА_i= {взятые дляi-й игры три мяча – новые},i= 1, 2, 3. Тогда…

Пример 4.6.В урне 3 белых и 4 черных шара. Два игрока поочередно вынимают из урны наудачу по шару, не вкладывая их обратно. Выигрывает тот игрок, который раньше вытащит белый шар. Определить вероятность выигрыша 1-го игрока, т.е. игрока, первым начавшим игру.

Решение. Испытание – из урны, содержащей 7 шаров, два игрока поочередно вынимают по одному шару, не возвращая их обратно, до тех пор, пока не будет вытащен белый шар. Пусть событиеA= {1-й игрок первым вытащит белый шар}.

4.7.Завод выпускает изделия определенного вида, причем 5% продукции завода в среднем составляет брак. Изделия осматриваются одним контролером; он обнаруживает имеющийся брак в среднем в 95% всех проверок. Если брак не обнаружен, изделие пропускается в готовую продукцию. Кроме того, контролер может по ошибке забраковать не бракованное изделие, что происходит в среднем в 7% всех проверок. Определить вероятность того, что изделие, наудачу выбранное из продукции завода, будет:

1. забраковано; b) забраковано ошибочно;

c) пропущено в готовую продукцию с браком.

Пример 4.8.Завод выпускает изделия определенного вида, причем 5% продукции завода в среднем составляет брак. После изготовления изделия последовательно осматриваются 4 контролерами;k-й контролер обнаруживает брак, если он имеется, в среднем в (91 +k)% ,k= 1, 2, 3, 4, всех проверок. Определить вероятность того, что изделие, наудачу выбранное из продукции завода, будет забраковано:

a) всеми контролерами;b) только четвертым контролером;

2. каким-либо одним контролером; d) хотя бы одним контролером.

Пример 4.9.Уходя из квартиры, восемь гостей, имеющих одинаковые размеры обуви, надевают туфли в темноте. Каждый из них может отличить правую туфлю от левой, но не может отличить свою от чужой. Найти вероятность того, что каждый гость наденет:

a) свои туфли;b) туфли из одной пары (может быть и не свои).

Пример 4.10.Та же задача, но гости не могут отличить не только свою туфлю от чужой, но и правую от левой и поэтому берут первые две попавшиеся туфли.