
Лекцция 3 для готово для презент
.docx
Лекция 3
Дифференцируемость функции многих переменных.
Производные и дифференциалы высших порядков.
Геометрические приложения частных производных.
Геометрический смысл первого дифференциала
П.1. Производные высших порядков.
Теорема о равенстве смешанных производных
Пусть дана
дифференцируемая функция n
переменных
u(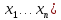 .
Пусть также вычислена производная
первого порядка по переменной
.
Пусть также вычислена производная
первого порядка по переменной
 . Эта функция тоже зависит от переменных
. Эта функция тоже зависит от переменных
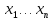 .
.
Возьмем от
 производную по переменной
производную по переменной
 :
:
 =
= .
.
Функция
 называется
частной производной второго порядка
от функции u(
называется
частной производной второго порядка
от функции u(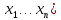 по
переменным
по
переменным


Таким же образом можно определить производные и третьего порядка .
Таким образом, справедлива рекуррентная формула
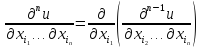 .
.
Производная
 называется смешанной, если среди
переменных
называется смешанной, если среди
переменных есть несовпадающие.
есть несовпадающие.
Пример.
Рассмотрим функцию двух переменных
 . Производные
. Производные
 ,
,
 являются несмешанными производными,
являются несмешанными производными,
 ,
,
 -
смешанными производными.
-
смешанными производными.
Теорема (о равенстве смешанных производных).
Пусть
1)
функция
 определена в некоторой окрестности
точки
определена в некоторой окрестности
точки
 ;
;
2)
существуют частные производные
 ,
,
 ,
,
 ,
,
 в этой окрестности;
в этой окрестности;
2)
производные второго порядка
 ,
,
 непрерывны в точке
непрерывны в точке
 .
.
Тогда
 в точке
в точке
 .
.
Доказательство.
Рассмотрим вспомогательное выражение:
 .
.
Здесь h,k -достаточно малые чтобы оставаться в пределах окрестности из пунктов 1)-2).
Введем вспомогательную
функцию

 (*).
(*).
Очевидно,

Но
 непрерывна в точке
непрерывна в точке
 .
.
Пусть
 .
Тогда
.
Тогда
 .
.
Рассмотрим выражение, аналогичное предложенному выше:
 ,
,
где
 .
.
Аналогично
получаем, что при
 выполнено
выполнено
 .
.
Следовательно,
 .
.
▲
Справедлива следующая общая теорема.
Теорема ( без доказательства).
Пусть
функция
 определена в области
определена в области
 .
Пусть существуют и непрерывны все
частные производные до k
-го порядка включительно в области
.
Пусть существуют и непрерывны все
частные производные до k
-го порядка включительно в области .
Тогда смешанные производные до -го
порядка не зависят от порядка
дифференцирования.
.
Тогда смешанные производные до -го
порядка не зависят от порядка
дифференцирования.
Пример. Рассмотрим функцию двух переменных, у которой смешанные производные второго порядка существуют, но не равны в точке (0,0):

Имеем:


Видим,
что

П.2. Дифференциалы высших порядков.
Неинвариантность дифференциалов порядка выше первого
Рассмотрим
дифференцируемую функцию n
переменных
 .
Вычислим ее первый дифференциал:
.
Вычислим ее первый дифференциал:

В правой части
этого равенства стоит функция от
переменных
 ,
,
 - некоторые фиксированные постоянные.
Возьмем дифференциал от левой и правой
частей:
- некоторые фиксированные постоянные.
Возьмем дифференциал от левой и правой
частей:
Формально можно записать:

Аналогично,

Вообще, справедлива формула:

Рассмотрим
функцию двух переменных
 .
Запишем формулы первого, второго и
третьего дифференциалов этой функции:
.
Запишем формулы первого, второго и
третьего дифференциалов этой функции:



Исследуем,
является ли дифференциал порядка выше
первого инвариантной величиной. Пусть
функция
 является сложной функцией переменных
является сложной функцией переменных

 x=x(u,v),
y=y(u,v);
x=x(u,v),
y=y(u,v);
Справедлива формула второго дифференциала:
 (*)
(*)
Докажем, что
нельзя записать, как это мы делали для
первого дифференциала, что то есть форма второго дифференциала
зависит от того, являются ли используемые
переменные зависимыми или нет.
то есть форма второго дифференциала
зависит от того, являются ли используемые
переменные зависимыми или нет.
Имеем:
 {так как первый
дифференциал инвариантен}=
{так как первый
дифференциал инвариантен}=

Если
бы
 были независимыми переменными, то была
бы справедлива формула, аналогичная
формуле (*). Но в нашем случае, когда
были независимыми переменными, то была
бы справедлива формула, аналогичная
формуле (*). Но в нашем случае, когда
 являются в свою очередь некоторыми
функциями, видим, что форма второго
дифференциала меняется, появляются два
новых слагаемых
являются в свою очередь некоторыми
функциями, видим, что форма второго
дифференциала меняется, появляются два
новых слагаемых
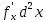 и
и
 . Видим, что форма второго дифференциала
неинвариантна.
. Видим, что форма второго дифференциала
неинвариантна.
Однако, существует частный случай, когда можно говорить, что форма второго дифференциала инвариантна. Это случай линейной замены переменных:

Отсюда в случае
линейной замены переменных действительно
получаем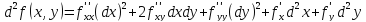
П.3. Геометрические приложения частных производных.
Касательный вектор к кривой. Нормаль к поверхности.
Касательная плоскость
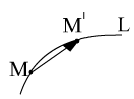
1) Касательный вектор. Рассмотрим кривую L в пространстве, заданную параметрическими уравнениями:

Фиксируем некоторое
значение
 ,
тем самым фиксируем некоторую точку M
на кривой L
:
,
тем самым фиксируем некоторую точку M
на кривой L
:
 Придадим переменной t
некоторое приращение
Придадим переменной t
некоторое приращение
 ,
получим точку
,
получим точку
 Рассмотрим вектор
Рассмотрим вектор




Пусть
 .
Тогда из рисунка мы видим, что вектор
.
Тогда из рисунка мы видим, что вектор
 направлен по касательной к кривой
направлен по касательной к кривой
 ,
в пределе можно записать формулу
,
в пределе можно записать формулу

Вектор
 является
касательным вектором к кривой L
.
является
касательным вектором к кривой L
.
2)
Касательная
плоскость к поверхности
 .
.
Пусть задана
поверхность

Пусть
точка
 - произвольная точка на поверхности
- произвольная точка на поверхности
 то
есть ее координаты удовлетворяют
уравнению поверхности
то
есть ее координаты удовлетворяют
уравнению поверхности
 .
.
Проведем через
точку M кривую L,
целиком лежащую на поверхности
 :
:
 .
.
Строим
 -
касательный вектор к кривой L
в точке M.
Пусть кривая L
имеет следующие параметрические
уравнения:
-
касательный вектор к кривой L
в точке M.
Пусть кривая L
имеет следующие параметрические
уравнения:


Но
 Функция
Функция
 одной переменной
t
тождественно равна 0 на отрезке [a,b]
одной переменной
t
тождественно равна 0 на отрезке [a,b]
Здесь мы ввели
вектор
 - градиент функции
- градиент функции
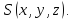
Вектор
 перпендикулярен касательному вектору
ко кривой L
в точке M.
перпендикулярен касательному вектору
ко кривой L
в точке M.
Соотношение
( верно для любой кривой L,
проходящей через точку M
целиком лежащей на поверхности
верно для любой кривой L,
проходящей через точку M
целиком лежащей на поверхности
 .
Таким образом, вектор
.
Таким образом, вектор
 направлен вдоль нормали к поверхности
S
в точке M.
направлен вдоль нормали к поверхности
S
в точке M. 
Учитывая этот
факт, получаем, что касательная
плоскость к поверхности
 в
точке
в
точке
 имеет
уравнение:
имеет
уравнение:

Рассмотрим L
- нормаль к поверхности
 в точке
в точке
 .
Вектор
.
Вектор
 является направляющим вектором этой
прямой, отсюда выписываем уравнение
нормали к поверхности
является направляющим вектором этой
прямой, отсюда выписываем уравнение
нормали к поверхности
 в точке
в точке
 :
:
 -
уравнение нормали к поверхности.
-
уравнение нормали к поверхности.
Замечания.
1)
Пусть поверхность
 задана явно:
задана явно:
 этом случае
уравнение касательной плоскости к
поверхности
этом случае
уравнение касательной плоскости к
поверхности
 имеет вид:
имеет вид:

Нормаль
к поверхности
 имеет
уравнение:
имеет
уравнение:

2)
Если в точке
 выполнено
выполнено
 или хотя бы одна из частных производных
не существует в этой точке, то касательная
плоскость в точке
или хотя бы одна из частных производных
не существует в этой точке, то касательная
плоскость в точке
 не существует.
не существует.
Рассмотрим геометрический смысл первого дифференциала. Используем результаты, полученные выше.
Рассмотрим функцию
двух переменны
 .
Пусть точка
.
Пусть точка
 принадлежит области определения функции
z.
Тогда точка
принадлежит области определения функции
z.
Тогда точка
 лежит на
поверхности
лежит на
поверхности
 Фиксируем
приращения
Фиксируем
приращения
 .
Имеем:
.
Имеем:



точка
N
лежит на поверхности, точка M
лежит на плоскости, касающейся поверхности
в точке
 :
:
Пусть P
касательная
плоскость к поверхности
 в точке
в точке


Пусть точка
 ,
, где координата
где координата
 удовлетворяет уравнению плоскости P.
удовлетворяет уравнению плоскости P.
Имеем:


Отсюда получаем геометрический смысл первого дифференциала:
первый
дифференциал
 геометрически
равен приращению аппликаты точки
приращению
аппликаты точки касательной плоскости,
если переменным
геометрически
равен приращению аппликаты точки
приращению
аппликаты точки касательной плоскости,
если переменным
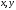
приданы
приращения

Если функция z
дифференцируема
в точке ,
то верно соотношение ( точки K
и N
имеют совпадающие проекции на плоскость
OXY
)
,
то верно соотношение ( точки K
и N
имеют совпадающие проекции на плоскость
OXY
)



