
термех 2 часть
.docx|
Билет
№8 Плоскопараллельное движение
тела
Плоскопараллельным (или
плоским) называется такое движение
твердого тела, при котором все его
точки перемещаются в плоскостях,
параллельных некоторой неподвижной
плоскости. Поэтому для изучения
движения всего тела достаточно изучить,
как движется сечение тела в плоскости
OXY. При движении тела величины Скорости
точек тела при плоскопараллельном
движении.
Теорема
1. Абсолютная
скорость любой
точки плоской фигуры в каждый данный
момент равна геометрической сумме
двух скоростей: скорости
поступательного движения плоской
фигуры и вращательной скорости во
вращательном движении фигуры.
Положение
любой точки тела можно определить
равенством
Взяв
производную от обеих частей уравнения
по времени получим, ,
где Теорема
3.
Плоская фигура в каждый момент времени
имеет одну точку, абсолютная скорость
которой равна нулю. Эта точка называется
мгновенным центром скоростей (МЦС).
Скорости точек плоской фигуры пропорциональны расстояниям от них до мгновенного центра скоростей. Если за полюс выбран МЦС, то скорость любой точки плоской фигуры есть вращательная скорость вокруг МЦС. Модуль скорости пропорционален расстоянию от точки до МЦС. Зная для данного момента времени положение МЦС и скорость какой-либо точки плоской фигуры, можно определить угловую скорость и скорость любой точки плоской фигуры. Если известна по модулю и направлению скорость одной точки и направление скорости другой точки, то можно определить скорости всех точек плоской фигуры. Частные случаи определения положения МЦС. Если угловая скорость плоской фигуры равна нулю, то МЦС удален в бесконечность и тело совершает мгновенно- поступательное движение. Скорости всех точек плоской фигуры равны по величине и направлению. Если скорости двух точек плоской фигуры параллельны между собой и перпендикулярны линии, соединяющей эти точки, то МЦС можно найти из условия пропорциональности скоростей точек расстояниям от этих точек до МЦС. При
качении без скольжения одного тела
по поверхности другого неподвижного
тела МЦС совпадает с точкой соприкосновения
тел, так как при отсутствии скольжения
скорость точки соприкосновения равна
нулю.
Определение
ускорений точек тела. Абсолютное
ускорение любой точки плоской фигуры
равно геометрической сумме ускорения
полюса и ускорения точки во вращательном
движении фигуры вокруг полюса.
Движение
плоской фигуры задано |
№9 Сложное движение точки Основные понятия и определения. Движение точки относительно неподвижной системы координат называется абсолютным движением точки. Движение точки относительно подвижной системы координат называется относительным движением точки. Движение подвижной системы координат в неподвижной системе координат называется переносным движением. Теоремы о сложении скоростей точки и об абсолютной производной вектора.
Сумма называется относительной или локальной производной:
Теорема о локальной производной. Абсолютная производная вектора равна сумме относительной (локальной) производной вектора и векторного произведения угловой скорости подвижной системы координат на сам этот вектор.
Подставляя (7) в выражение (1), имеем
Выделим переносную скорость точки, используя прием замораживания. Тогда после останова точки ее относительная скорость равна нулю Vr = 0, а абсолютная скорость равна ее переносной скорости V = Ve, так как остановленная в относительном движении точка (вмороженная в подвижную систему координат) продолжает перемещаться в неподвижной системе координат за счет переносного движения подвижной системы координат. Учитывая это, из выражения (8) имеем
Абсолютная
скорость точки, участвующей в сложном
движении, равна геометрической сумме
ее относительной и переносной скоростей.
Теорема о сложении ускорений (теорема Кориолиса).
Абсолютное
ускорение точки, участвующей в сложном
движении, равно геометрической сумме
относительного, переносного и
кориолисова ускорений.
Величина кориолисова ускорения вычисляется по формуле
а направление вектора определяется по правилу построения вектора векторного произведения векторов ωe и Vr
|
|||||||||||||||||||||
|
№11 Центр масс системы материальных точек ЦЕНТР
МАСС (центр
инерции) системы материальных точек
– условная (или эквивалентная) точка,
представляющая собой одну из
геометрических характеристик
распределения масс в системе. Пусть
Момент инерции тела зависит от:
Теорема Гюйгенса-Штейнера Момент инерции тела относительно произвольной оси (I) равен сумме момента инерции Ic относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела М на квадрат расстояния между осями: I = Ic + Ma2, где а — расстояние между осями.
|
||||||||||||||||||||||
|
№10 Законы Ньютона. Основные законы динамики. Законы Галилея - Ньютона 1.
Закон
инерции:
изолированная материальная точка
неспособна вывести себя из состояния
покоя или равномерного прямолинейного
движения без воздействия внешних сил
или полей;2. Основной
закон динамики:
сила, действующая на тело, сообщает
ей ускорение, которое в инерциальной
системе отсчета пропорционально
величине силы и совпадает с ней по
направлению:
Дифференциальные уравнения движения свободной материальной точки в декартовых координатах Метод
кинетостатики:
если к движущейся под действием сил
точке приложить силу инерции, то
геометрическая сумма всех сил будет
равна нулю:
Так
как:
Основные задачи динамики точки 1. Зная массу материальной точки и уравнение ее движения определить модуль и направление равнодействующей силы, под действием которой точка движется. 2. Зная силы, действующие на материальную точку, ее массу и начальные условия движения определить траекторию.
|
|
|||||||||||||||||||||
|
№12 Кинетическая энергия материальной точки. Теорема Кёнига Кинетическая
энергия системы есть энергия движения
центра масс плюс энергия движения
относительно центра масс:
Теорема об изменении кинетической энергии материальной точки Кинетическая энергия материальной точки - скаляр, равный половине произведение массы точки на квадрат ее скорости. Теорема: изменение кинетической энергии материальной точки на некотором перемещении равно работе силы, действующей на точку, на том же перемещении. Основное
уравнение динамики:
Работа Мерой действия силы при превращении механического движения в другую форму движения является работа силы.
Работа постоянной по модулю и направлению силы F на прямолинейном перемещении s ее точки приложения равна
Если угол α острый, то работа силы положительна, если тупой – отрицательна. Если направления силы и перемещения совпадают (α=0), то A = Fs; Если направление силы перпендикулярно направлению перемещения (α=90◦), то А = 0; Если направление силы противоположно направлению перемещения (α=180◦), то A = -Fs.
ПОТЕНЦИАЛЬНЫЕ СИЛЫ - силы, работа которых зависит только от начального и конечного положения точек их приложения и не зависит ни от вида траекторий, ни от закона движения этих точек. Примерами консервативных сил являются: сила тяжести, сила упругости, сила кулоновского (электростатического) взаимодействия Для консервативных сил выполняются следующие тождества:
|
Мощность Мощностью
называется работа, совершаемая силой
в единицу времени. Средняя мощность
Рср силы F за время Δt на перемещении
Δs, с которым сила образует угол α,
определяется по формуле Как
было указано, F cos α является
проекцией силы на направление движения
материальной точки. Обозначив F cos α
через Fv, получим
Кинетическая энергия механической системы при различных видах движения Кинетическая
энергия механической системы
- скаляр, равный сумме кинетических
энергий всех точек системы:
При
поступательном движении:
При
вращательном движении:
При
плоскопараллельном движении:
Теорема об изменении кинетической энергии механической системы
Теорема: изменение кинетической энергии механической системы на конечном перемещении равно сумме работ внешних сил на том же перемещении. Потенциальная энергия
Существуют
две основные формы механической
энергии: потенциальная энергия, или
энергия положения, и кинетическая
энергия, или энергия движения. Чаще
всего приходится иметь дело с
потенциальной энергией сил тяжести.
Потенциальной энергией силы тяжести
материальной точки или тела в механике
называется способность этого тела
или точки совершать работу при опускании
с некоторой высоты до уровня моря (до
какого-то уровня). Потенциальная
энергия численно равна работе силы
тяжести, произведенной при перемещении
с нулевого уровня до заданного
положения. Обозначив потенциальную
энергию
|
|||||||||||||||||||||
Для тела, вращающегося под действием силы вокруг оси, можно после разложения силы по естественным осям получить
δA = Fτ ⊗ δs ⊕ Fn ⊗ δs ⊕ Fb⊗ δs = F ⊗ δs.
Приняв δs
= r δφ,
получим δA
= Fτ ⋅
r ⋅ δφ
= M ⋅ δφ или
Если действующие силы и момент постоянны, то вышеприведённые формулы принимают вид
A =F ⊗ s, A = M ⋅ φ.
При качении тел по поверхностям возникает момент сопротивления качению, который определяется по формуле
Mсопр= N ⋅ fk ,
где N - нормальная реакция поверхности;
fk (или δ) - коэффициент трения качения.
Работа момента сопротивления качению всегда отрицательна:
A = -Mсопр ⋅ φ.
№13 Классификация связей
Несвободная материальная точка - на движение наложены кинематические ограничения.
Связи - тела, ограничивающие свободу движения материальной точки. Динамические реакции связи - силы, с которыми связи действуют на движущуюся материальную точку.
Классификация связей:
1. стационарные - уравнения которых не содержат t в явном виде и нестационарные.
2. голономные - ограничивающие только свободу перемещения, а не скорость и неголономные.
3. неудерживающие - препятствующие движению в одном направлении и допускающие в противоположном и удерживающие.
Виртуальные (возможные) и действительные перемещения.
Рассмотрим бесконечно малые перемещения точек системы, совместимые со связями, наложенными на систему. Среди этих перемещений будем различать два вида перемещений - виртуальные и действительные.
Рассмотрим виртуальное перемещение точки системы с номером i. Виртуальным перемещением δri называется мысленное бесконечно малое перемещение точки, допускаемое связями без их разрушения в данное фиксированное мгновение времени.
Если связь одна и описывается уравнением (2), физически ясно, что связь не нарушится, когда вектор виртуального перемещения
|
|
(3) |
будет лежать в плоскости, касательной к поверхности связи, зафиксированной в данное мгновение времени. Математически это условие выражается как
|
|
(4) |
где grad f - градиент функции (2) при фиксированном t, перпендикулярный поверхности связи в месте нахождения точки, равный
|
|
(5) |
Учитывая выражения (3) и (5), раскрываем скалярное произведение в (4), получаем уравнение, которому должны удовлетворять проекции δxi, δyi, δzi виртуального перемещения δri, чтобы связь не нарушалась:
|
|
(6) |
В вариационном исчислении бесконечно малые величины δri, δxi, δyi, δzi называются вариациями функций ri, xi, yi, zi. Изменения координат точек или уравнений связи при неизменном времени находятся синхронным варьированием, которое осуществляется согласно левым частям формул (4) и (6).
То есть проекции δxi, δyi, δzi виртуального перемещения точки δr обращают в нуль первую вариацию уравнения связи при условии, что время не варьируется (синхронное варьирование):
|
|
(7) |
Следовательно, виртуальное перемещение точки не характеризует ее движение, а определяет связь или, в общем случае, связи, наложенные на точку системы. Таким образом, виртуальные перемещения позволяют учесть эффект механических связей, не вводя реакции связей, как мы это делали раньше, и получать уравнения равновесия или движения системы в аналитическом виде, не содержащие неизвестных реакций связей.
Не следует путать виртуальное перемещение точки с ее элементарным действительным перемещением dri = Vidt, которое действительно происходит за элементарный промежуток времени dt и направлено, как и скорость Vi, по касательной к траектории движения точки.
Отметим еще ряд особенностей виртуальных и действительного перемещения точки:
а) у точки имеется только одно элементарное действительное перемещение, а виртуальных перемещений у точки может быть несколько и даже бесконечно много, например в случае, когда на точку наложена только одна голономная связь;
b) если голономная связь нестационарная, то элементарное действительное перемещение не совпадает ни с одним из виртуальных перемещений точки;
c) если голономная связь стационарна, то элементарное действительное перемещение точки совпадает с одним из ее виртуальных перемещений.
Последние два
утверждения можно доказать аналитически,
однако это можно показать графически
на примере рассмотренных голономных
связей (рис. 59, b и c).
На рис. 60, a изображена нестационарная связь (подвижная связь) в моменты времени t - Δt, t, t + Δt, где t - фиксированное значение времени, когда определяются виртуальные перемещения, а Δt - приращение времени. Там же построены: действительная траектория бусинки, уравнение которой не совпадает с уравнением связи в момент времени t из-за движения бусинки; скорость бусинки V, направленная по касательной к действительной траектории, и вектор элементарного действительного перемещения dr, который не совпадает ни с одним из виртуальных перемещений δr, направленных по касательной к связи в момент времени t. На рис. 60, b показана стационарная связь, где бусинка движется по неподвижной связи, ее скорость всегда направлена по касательной к связи, за счет чего элементарное действительное перемещение dr совпадает с одним из виртуальных перемещений δr.

 ,
масса - мера инертности точки:
,
масса - мера инертности точки:
 .3.
Закон
равенства действия и противодействия;4.
Закон про
равнодействующую силу:
несколько одновременно действующих
на точку сил сообщают ей такое ускорение,
какое сообщает ей одна сила, равная
их геометрической сумме:
.3.
Закон
равенства действия и противодействия;4.
Закон про
равнодействующую силу:
несколько одновременно действующих
на точку сил сообщают ей такое ускорение,
какое сообщает ей одна сила, равная
их геометрической сумме:
 .
. ,
где Ф - сила инерции.
,
где Ф - сила инерции. ,
то проектируя на ось координат
получаю:
,
то проектируя на ось координат
получаю: ,
так как:
,
так как:
 то аналогично для y и z получаю:
то аналогично для y и z получаю:
 ,
домножим на элементарное перемещение:
,
домножим на элементарное перемещение:
 ;
;
 ;
;
 .
Интегрируя полученное выражение:
.
Интегрируя полученное выражение:

 .
.

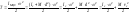 ,
где d - расстояние от центра масс до
МЦС.
,
где d - расстояние от центра масс до
МЦС. ,
так как работа внутренних сил равна
нулю, то:
,
так как работа внутренних сил равна
нулю, то:
 .
.