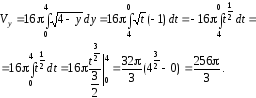- •Г. В. Красоленко, н. В. Сванидзе, г. В. Якунина
- •Введение
- •Фамилия, имя, отчество
- •Интегральное исчисление в случае функции одной переменной. Формула Тейлора и Маклорена. Гиперболические функции
- •Примерный вариант контрольной работы № 3 по дифференциальному исчислению в случае функции одной переменной
- •Решение задачи № 1
- •Решение задачи № 2
- •Решение задачи № 3
- •Решение задачи № 4
- •Примерный вариант контрольной работы № 4 по интегральному исчислению в случае функции одной переменной
- •Решение задачи № 1
- •Решение примера а)
- •Решение примера в)
- •Решение задачи № 2
- •Решение задачи № 4
- •Решение задачи № 4
- •Контрольная работа № 3 по дифференциальному исчислению функций одной переменной
- •Контрольная работа № 4 по интегральному исчислению функции одной переменной
- •Рекомендуемая литература
- •Оглавление
- •Диффренциальное и интегральное исчисление в случае функцииодной переменной
- •190005, Санкт-Петербург, 2-я Красноармейская ул., д. 4.
Решение примера в)
В этом примере применяются методы интегрирования тригонометрических функций (см. [1], [2] и [6]).
Для
вычисления интеграла
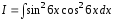 применим
следующие тригонометрические формулы
применим
следующие тригонометрические формулы
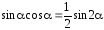 и
и

Тогда
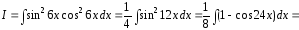
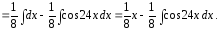
Последний
интеграл
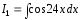 вычислим с помощью замены переменной
вычислим с помощью замены переменной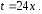
Тогда
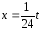 и
и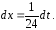 В результате получаем
В результате получаем
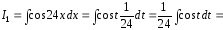
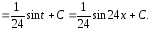
Ответ
примера в):

Решение задачи № 2
В
этой задаче нужно вычислить площадь
фигуры, ограниченной линиями
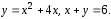
Построим заданную фигуру (см. рис. 3). Найдем точки пересечения указанных в условии линий. Решим для этого систему уравнений
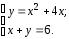
Она равносильна системе
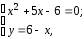 откуда
откуда
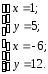
Уравнение
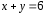 задает прямую, которая проходит через
две найденные точкиc
координатами
задает прямую, которая проходит через
две найденные точкиc
координатами
 и
и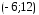 .
.
Уравнение
параболы
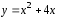 приведём к каноническому виду, выделяя
полный квадрат по переменной
приведём к каноническому виду, выделяя
полный квадрат по переменной ,
,
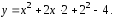
Тогда каноническое уравнение параболы имеет вид
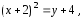
из
которого видно, что парабола имеет осью
симметрии вертикальную прямую
 ,
вершину в точке
,
вершину в точке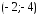 и ветви параболы направлены вверх (в
направлении оси
и ветви параболы направлены вверх (в
направлении оси ).
).
Для того, чтобы найти площадь построенной фигуры, надо сначала составить выражение бесконечно малого элемента искомой площади, а затем проинтегрировать полученный результат в пределах изменения аргумента (см. [7]).
Обозначим
бесконечно малый элемент площади через
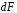 .
.
Он
равен площади прямоугольника,
заштрихованного на рис. 3, со сторонами
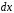 и
и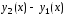 ,
т.е.
,
т.е.
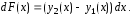
Так
как
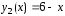 и
и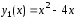 ,
то
,
то
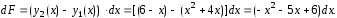

Искомую
площадь получаем, проинтегрировав
полученный результат в пределах изменения
переменной
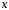 от
от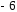 до
до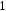 .
Тогда
.
Тогда
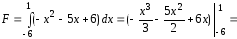
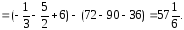
Решение задачи № 4
В
данной задаче нужно вычислить объём
тела, полученного вращением вокруг оси
 плоской фигуры, ограниченной параболой
плоской фигуры, ограниченной параболой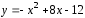 и прямой
и прямой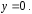
Чтобы построить параболу, ее уравнение
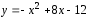 (1)
(1)
приведём
к каноническому виду, выделяя полный
квадрат по переменной
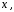 :
:
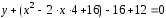 ,
,
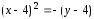 .
(2)
.
(2)
Следовательно,
парабола имеет ось симметрии
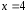 ,
вершину в точке
,
вершину в точке .
Ветви параболы направлены вниз (в
направлении, противоположном положительному
направлению оси
.
Ветви параболы направлены вниз (в
направлении, противоположном положительному
направлению оси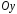 ).
Кривая пересекает ось
).
Кривая пересекает ось в точках
в точках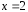 и
и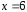 .
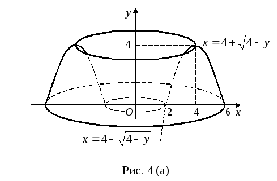
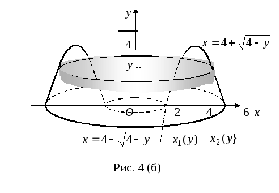
Заданная фигура заштрихована на рис. 4
(а). Вращая её вокруг оси
.
Заданная фигура заштрихована на рис. 4
(а). Вращая её вокруг оси ,
получим тело с полостью.
,
получим тело с полостью.
Найдем
объем
 тела вращения. Для этого составим
выражение бесконечно малого элемента
объема
тела вращения. Для этого составим
выражение бесконечно малого элемента
объема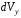 ,
а затем проинтегрируем полученный
результат в пределах изменения аргумента
(см. [7]).
,
а затем проинтегрируем полученный
результат в пределах изменения аргумента
(см. [7]).
Бесконечно
малый элемент искомого объема
 равен объему кольцевого цилиндра с
внешним радиусом
равен объему кольцевого цилиндра с
внешним радиусом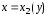 ,
внутренним радиусом
,
внутренним радиусом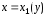 и высотой
и высотой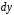 (см. рис. 4 (б), на котором выделен затененный
цилиндр):
(см. рис. 4 (б), на котором выделен затененный
цилиндр):
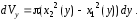 (3)
(3)
Рассечём
тело вращения плоскостью, перпендикулярной
оси
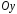 .
В сечении получим кольцо (рис. 4 (б)),
которое является основанием нашего
бесконечно тонкого кольцевого цилиндра.
Чтобы определить внутренний
.
В сечении получим кольцо (рис. 4 (б)),
которое является основанием нашего
бесконечно тонкого кольцевого цилиндра.
Чтобы определить внутренний и
внешний
и
внешний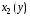 радиусы
этого кольца, вернемся к уравнению
параболы. Из уравнения (2) найдём
радиусы
этого кольца, вернемся к уравнению
параболы. Из уравнения (2) найдём
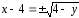 ,
,
следовательно,
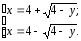
Очевидно, что первая функция задает внешний радиус кольца, а вторая – внутренний, т.е.
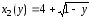 и
и
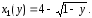
Найдём бесконечно малый элемент искомого объёма по формуле (3):
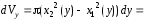
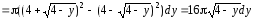 .
.
Для
вычисления объёма тела вращения
проинтегрируем полученный результат
по переменной
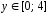 .
Тогда
.
Тогда
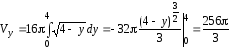 .
.
Для
вычисления интеграла сделаем подстановку
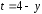 и используем теорему о замене переменной.
и используем теорему о замене переменной.
Найдем
пределы интегрирования по переменной
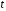 :
если
:
если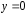 ,
то
,
то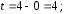 если
если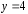 ,
то
,
то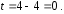
Так
как
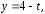 то
то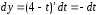 и в результате получаем
и в результате получаем