
Semenova_matem1
.pdf
2.3.4. Интегральная формула Коши
Теорема. Пусть функция f(z) аналитична в замкнутой односвязной области D, L – граница области, тогда имеет место формула
f(z0) = |
1 |
|
H |
f(z) |
dz; |
(2:5) |
||
2 i |
|
|||||||
|
z |
− |
z0 |
|
||||
z |
D |
D: |
||||||
где 0 |
|
|
L |
|
|
|
|
|
|
|
любая точка внутри области |
|
|||||
Зафиксируем произвольную точку z0. Построим окружность Lr
сцентром в точке z0 и малым радиусом r так, чтобы Lr D. Получим двусвязную область D1, ограниченную контурами L и Lr (рис. 2.8),
в которой подинтегральная функция f(z) аналитична.
z−z0
L
|
|
|
|
|
|
Тогда в силу замечания к тео- |
|||
|
|
LZ |
|
|
|
реме Коши имеем |
|
||
|
|
Z0 |
|
|
|
|
f(z) |
(z) |
|
|
|
|
|
|
|
|
I z − z0 dz = I |
zf− z0 dz |
|
|
|
|
|
|
|
|
L |
Lr |
|
|
|
|
|
|
|
отсюда: |
|
|
|
|
|
Рис. 2.8 |
|
|
|
|
|
|
|
1 |
I |
(z) |
1 |
I |
f(z) |
1 |
f(z) |
f(z ) + f(z ) |
|
2 i |
zf− z0 dz = |
2 i |
z − z0 dz = |
2 i |
I |
− z −0z0 |
0 dz = |
||
L Lr
= |
1 |
f(z0) I |
1 |
dz + |
1 |
|
I |
||
|
|
|
|
|
|
||||
2 i |
z − z0 |
2 i |
|||||||
|
|
Lr |
|
|
|
|
|
|
Lr |
|
= |
|
1 |
f(z )2 i + |
|
1 |
|||
|
|
|
|
|
|||||
|
|
|
2 i |
0 |
|
2 i |
|||
|
|
|
|
|
|||||
Lr
f(z) − f(z0) dz = [ пример 1] z − z0
I
f(z) − f(z0) dz: z − z0
|
|
H |
− |
|
|
|
|
|
Lr |
− |
|
|
|
|
|
|
|
|
|
|
LHr |
|
|
||||
Значит, |
1 |
|
f(z) |
dz |
− |
f(z |
0 |
) = |
1 |
f(z) − f(z0) |
dz: |
||
2 i L |
z z0 |
|
|
2 i |
z |
|
z0 |
||||||
По условию теоремы, функция f(z) аналитична, т.е. f(z) непрерывна в точке z0 D, значит, для любого " > 0 найдется > 0, такое, что для всех z D, удовлетворяющих условию |z − z0| < , следует выполнение
31

неравенства |f(z) − f(z0)| < ".
Зафиксируем " > 0, по нему подберем > 0 и возьмем в качестве
радиуса r окружности Lr число r : |
r < , тогда |z − z0| ≤ r < , тогда |
||||||||||||||||||||||||||||||
для них |f(z) − f(z0)| < ", поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1 |
|
f(z) |
dz |
|
f(z0) |
= |
|
|
1 |
|
|
f(z) − f(z0) |
dz |
|
||||||||||||||||
2 i I |
|
− |
2 i I |
|
|
|
|
|
≤ |
||||||||||||||||||||||
|
z |
− |
z0 |
|
|
|
|
|
|
|
|
|
|
|
|
z |
− |
z0 |
|
||||||||||||
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Lr |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
f |
(z) |
|
|
f(z0) |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
− |
| |
|
dz |
|
|
|
< |
|
|
|
||||
|
|
|
|
≤ |2 i| I |
|
|
|
|z − z0| |
| |
| |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Lr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< [ если z Lz; то|z − z0| = r] < |
1 " |
· |
2 r = ": |
|
||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||
|
2 |
r |
|
||||||||||||||||||||||||||||
При " → 0 получаем,что |
|
|
1 |
|
|
f(z) |
dz − f(z0) = 0: |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
2 i L |
z |
− |
z0 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Интеграл (2:5) называется интегралом Коши, а сама формула –
интегральной формулой Коши.
Замечание. Формула Коши позволяет находить значение аналитической функции f(z) в любой точке z0, лежащей внутри области D, через ее значения на границе этой области.
Теорема. Для всякой дифференцируемой в точке z0 функции f(z) существуют производные всех порядков, причем про-
изводная порядка n имеет вид
f(n)(z0) = |
n! |
|
f(z) |
dz. |
|
|
|
|
|||
2 i |
|
(z z )n+1 |
|||
|
|
L |
− |
0 |
|
|
|
H |
|
|
|
Теорема. В окрестности каждой точки z0, где существует производная f0(z), функция f(z) может быть представлена
сходящимся рядом
f(z) = f(z0) + f0(z0)(z − z0) + f00(z0) (z − z0)2 + : : :
2!
: : : + f(n)(z0) (z − z0)n + : : : (2.6)
n!
32
Следствие. Производная аналитической функции также является аналитической функцией.
Замечание. Ряд (2.5) называется рядом Тейлора функции f(z)
в точке z0. При этом ряд Тейлора функции комплексного переменного существует и сходится к самой функции. Ряд Тейлора для действительной функции f(x) может сходиться к другой функции или быть расходящимся.
2.4. Ряды в комплексной плоскости
Числовые ряды
|
|
∞ |
|
|
|
|
|
|
|
Ряд |
un, членами которого являются комплексные числа, называ- |
||||||||
|
|
n=1 |
|
|
|
|
|
|
|
ется |
числовым рядом в комплексной области. Такой ряд можно записать |
||||||||
|
∑ |
∑ |
n |
|
|
|
|
|
|
|
n∑ |
|
|
|
|
|
|||
|
|
∞ |
∞ |
|
|
|
|
|
|
в виде |
un = |
(ai + ibi), где ai и bi — действительные числа. Сумма |
|||||||
|
n=1 |
n=1 |
∑ |
|
|
|
|
|
|
|
∑ |
∑ |
|
|
|
|
|
||
|
|
|
n |
bk первых n членов называется частичной |
|||||
Sn = |
uk = |
ak + i |
|||||||
|
k=1 |
k=1 |
k=1 |
|
|
|
|
|
|
суммой ряда. |
|
|
|
|
|
|
|
||
Если существует конечный предел S последовательности {Sn} ча- |
|||||||||
|
|
|
|
∞ |
|
|
|
|
|
стичных сумм ряда, то ряд |
un называется сходящимся, число S – |
||||||||
|
|
|
|
n=1 |
|
|
S |
|
частичных сумм |
|
|
|
|
последовательности |
{ |
n} |
|||
суммой ряда. Если же предел∑ |
|
|
|
||||||
ряда не существует или бесконечен, то ряд называется расходящимся.
|
|
Теорема. Ряд |
∞ |
un сходится тогда и только тогда, когда |
|
|
||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
=1 |
|
|
∞ |
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
n∑ |
|
|
|
|
|
|
||
|
|
сходится каждый из рядов |
an и |
bn. При этом |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
n=1 |
|
|
|
|
|
S = S |
1 |
+ iS |
, где |
S |
и |
S |
2 |
суммы соответствующих рядов в |
|
|
||||
|
|
|
|
|
2 |
1 |
|
–∑ |
∑ |
|
|
|
||||
|
|
действительной области. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание. Таким образом, исследование сходимости ряда |
∞ |
||||||||||||||
|
un = |
|||||||||||||||
∞ |
∞ |
|
|
|
|
|
|
|
|
|
=1 |
|
|
|||
|
|
∞ |
|
∞ |
|
|
|
n∑ |
||||||||
n∑ |
∑ |
bn |
с |
|
|
|
|
|
|
|
||||||
an + i |
|
|
комплексными членами сводится к исследованию |
|||||||||||||
=1 |
|
|
n=1 |
n∑ |
|
∑ |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
bn с действительными членами. Значит, |
|||||||||
сходимости рядов |
an и |
|
|
|||||||||||||
|
|
|
|
|
|
|
=1 |
|
n=1 |
|
|
|
|
|
|
|
33
основные определения и теоремы аналогичны соответствующим определениям и теоремам из теории рядов с действительными членами.
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
k=∑ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
Остатком ряда |
un называется rn = |
|
uk: |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
n+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
Теорема. (Необходимый признак сходимости ряда.) Если |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ряд |
un сходится, то его общий член un стремится к нулю |
|
|
||||||||||||||||||||
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при n∑ |
|
, т.е. lim un = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
→ ∞ |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n∑ |
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ряд |
un называется абсолютно сходящимся, если сходится ряд, |
||||||||||||||||||||||||
|
|
|
=1 |
|
|
|
|
n∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
составленный из его модулей: |
|
|un|: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема. Если ряд |
∞ |
un абсолютно сходится, то он и |
|
|
||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
просто сходится. |
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
n∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По условию теоремы ряд |
∞ |
∞ |
|
|
|
|
|
сходится. Так как |
|||||||||||||||||
|
|
|
|un| = |
|
an2 + bn2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
=1 |
n=1 |
√ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|an| ≤ |
2 |
2 |
и |bn| ≤ |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
an |
+ bn |
an + bn, то в силу первого признака сравнения |
|||||||||||||||||||||||
|
|
|
|
|
|
∞ |
|
∞ |
|
|
|
∑ |
|
|
|
|
n∑ |
|
|
|
|
|
|
|||
для |
рядов с действительными членами ряды |
∞ |
|
|
и |
∞ |
|
|
|
сходятся, |
||||||||||||||||
|
a |
n |
|
|
b |
n |
|
|||||||||||||||||||
|
|
√ |
|
|
|
|
√ |
|
|
|
| |
| |
|
|
| |
|
| |
|
|
|
||||||
|
|
|
|
|
n∑ |
∞ ∑ |
|
|
|
n=1 |
|
|
|
|
=1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
а значит, ряды |
|
|
an и |
|
bn сходятся абсолютно, т.е. и просто сходятся. |
|||||||||||||||||||||
|
|
|
|
|
|
=1 |
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Следовательно, ряд |
un сходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У абсолютно |
сходящихся рядов с комплексными членами возможна |
||||||||||||||||||||||||
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
перестановка членов ряда, что не влияет на сумму ряда. Кроме того, такие ряды можно почленно складывать и перемножать.
Степенным рядом в комплексной области называют ряд вида
∑∞
Cnzn; |
(2:7) |
n=1
где Cn – комплексные числа; z = x + iy – комплексная переменная.
∑∞
Замечание. Степенной ряд общего вида Cn(z − z0)n, где z0 –
n=1
комплексное число, подстановкой t = z − z0 сводится к ряду (2.7).
34

Ряд (2.7) при одних значениях аргумента z может сходиться, а при других – расходиться.
Совокупность всех значений z, при которых ряд (2.7) сходится, называется областью сходимости этого ряда.
Теорема Абеля. Если степенной ряд (2.7) сходится при z = z0 (z0 =6 0), то он абсолютно сходится при всех значениях z, удовлетворяющих условию |z| < |z0|:
Следствие. Если ряд (2.7) расходится при z = z0, то он расходится при всех значениях z, удовлетворяющих условию |z| > |z0|:
Из теоремы Абеля следует, что для каждого степенного ряда (2.7) существует действительное число R, называемое радиусом сходимости,
R : 0 ≤ R ≤ ∞. При этом внутри круга |z| < R, называемом
кругом сходимости, находятся все точки сходимости ряда (2.7), а во всех точках вне этого круга ряд (2.7) расходится. Кроме того, в точках окружности |z| = R ряд (2.7) может как сходиться, так и расходиться.
|
|
1 |
|
|
Cn |
|
|
R = |
|
. |
|
|
|
|
|
Радиус сходимости можно вычислить по формуле R = n→∞ |
|
Cn+1 |
|
или |
|||
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
||
|
√ |
|
|
|
|
|
|
|
nlim |Cn| |
|
|
|
|
||
|
|
→∞ |
|
|
|
|
|
Свойства степенного ряда: |
|
|
|
|
|||
1◦ |
сумма степенного ряда внутри круга его сходимости есть аналити- |
||||||
|
ческая функция. |
|
|
|
|
||
2◦ |
степенной ряд внутри круга сходимости можно почленно диффе- |
||||||
|
ренцировать и интегрировать любое число раз. Полученный ряд |
||||||
|
имеет тот же радиус сходимости, что и исходный ряд. |
|
|
|
|
||
35
2.4.1. Ряд Тейлора
Теорема. Всякая аналитическая в круге |z − z0| < R
функция f(z) может быть единственным образом разложена в этом круге в степенной ряд
|
∞ |
|
|
|
|
|
(2.8) |
||
f(z) = n=1 Cn(z − z0)n; |
|||||||||
коэффициенты которого определяются формулами |
|||||||||
|
∑ |
|
|
|
|
|
f( ) |
||
|
f |
(n) |
(z0) |
1 |
|
||||
|
|
|
|
d , где Lr — произвольная |
|||||
Cn = |
|
|
|
= |
|
|
|
||
|
n! |
2 i |
|
n+1 |
|||||
окружность с |
|
|
Lr |
( − z0) |
|||||
центром |
в точке z , лежащая внутри круга |
||||||||
|
|
|
|
|
|
|
H |
0 |
|
сходимости, причем такое представление единственно.
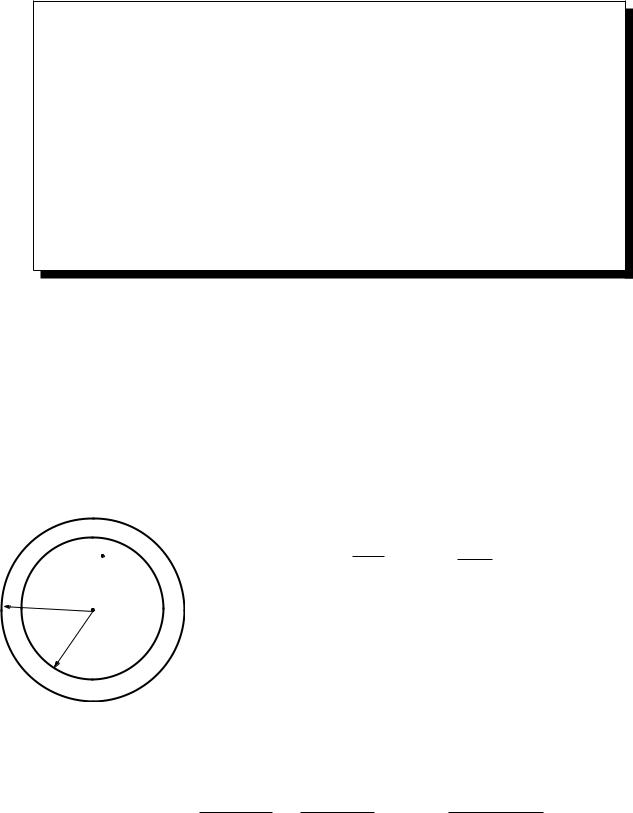
Пусть функция f(z) аналитична в круге |z − z0| < R. Рассмотрим окружность Lr с центром в точке z0 и радиусом r < R (рис 2.9). Пусть фиксированная точка z лежит внутри круга, т.е. z : |z − z0| < r. Отметим,что функция f(z) аналитична, в том числе и на окружности Lr, и внутри нее, поэтому к ней применима интегральная формула Коши:
f(z) = |
1 |
|
|
|
f( ) |
d в точке z, причем — точка окружности L . |
||||||||||||||||||||||||||||||
2 i LHr |
|
|
||||||||||||||||||||||||||||||||||
|
|
− z0 |
|
Отметим, что |
|
1 |
|
= |
|
|
1 |
|
|
|
= r |
|||||||||||||||||||||
|
|
|
|
|
|
−z |
( −z0)−(z−z0) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
−z0 |
a1 |
, — сумма |
||||||||||
|
|
|
|
Z |
|
= |
|
|
|
|
|
|
z z0 |
|
= |
|
|
|
|
|
z z0 |
= |
1 |
q |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
( −z0)(1− z0 ) |
1 |
− |
−−z0 |
|
− |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
геометрической прогрессии, где |
|
|
1 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
a1 = |
|
|
||||||||||||||||||||||||
R |
|
|
|
|
|
|
|
|
−z |
|||||||||||||||||||||||||||
|
|
|
|
Z0 |
|
|
|
|
– первый член геометрической прогрессии, |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
q |
|
= |
|
z−z0 — знаменатель геометрической |
||||||||||||||||||||||||
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
−z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
прогрессии. Так как z лежит внутри круга, |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
а — на окружности, т.е. |z−z0| < | −z0|, то |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
z−z0 |
|
|
< 1, а значит, прогрессия бесконечно |
|||||||||||||||||||||||
|
|
Рис. 2.9 |
|
|
−z0 |
|
|
|
|
|
Следовательно, |
имеет место |
||||||||||||||||||||||||
|
|
|
убывающая. |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
равенство: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
1 |
|
= |
|
1 |
|
+ |
z − z0 |
|
+ |
(z − z0)2 |
+ : : : + |
(z − z0)n |
+ : : : |
|
|
|||||||||||||||||||
− z |
− z0 |
( − z0)2 |
( − z0)3 |
( − z0)n+1 |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Умножим обе части равенства на |
|
|
1 |
f( ) и проинтегрируем по контуру |
||||||||||||||||||||||||||||||||
|
2 i |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
36

Lr, получим |
|
|
|
|
|||||
1 |
|
I |
( ) |
1 |
|
I |
|||
|
|
|
f |
d = |
|
|
|
||
2 i |
− z |
2 i |
|||||||
|
|
|
Lr |
|
|
|
|
|
Lr |
|
|
|
|
: : : + |
1 |
|
I |
||
|
|
|
|
|
|
||||
|
|
|
|
2 i |
|||||
Lr
|
( ) |
1 |
|
I |
f( ) |
||
|
f |
d + (z − z0) |
|
|
|
d + : : : |
|
− z0 |
2 i |
( − z0)2 |
|||||
Lr
f( )n+1 d (z − z0)n + : : : ;
( − z0)
∞ |
n |
1 |
|
|
|
|
f( ) |
|
|
|
|
|
|
|
|
|
|||
f(z) = |
(z − z0) |
|
|
|
|
|
|
|
d ; |
|
|
|
|
|
|||||
2 i |
|
( |
− |
z )n+1 |
|
|
f( ) |
||||||||||||
n∑ |
∞ |
|
LHr |
n |
|
|
0 |
|
|
1 |
|
|
|||||||
=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
т.е. f(z) = |
=0 Cn(z − z0) |
|
|
; где |
|
|
Cn = |
|
|
|
|
|
d ; причем, |
||||||
|
|
|
|
2 i |
|
( |
− |
z0)n+1 |
|||||||||||
|
n∑ |
|
|
|
|
|
|
|
|
f |
(n)(z0) |
|
|
LHr |
|
|
|||
учитывая разложение (2:6), Cn = |
|
|
|
|
. |
|
|
|
|
|
|
||||||||
n!
Докажем единственность разложения. Пусть функция f(z) в том же круге |z − z0| < R представлена другим степенным рядом
f(z) = b0 + b1(z − z0) + b2(z − z0)2 + : : : + bn(z − z0)n + : : :
Последовательно дифференцируя этот ряд, получаем
f0(z) = b1 + 2b2(z − z0) + 3b3(z − z0)2 + : : : + nbn(z − z0)n−1 + : : :
f00(z) = 2b2 + 6b3(z − z0) + : : : + n(n − 1)bn(z − z0)n−2 + : : :
: : :
f(n)(z) = n!bn + (n + 1)!bn+1(z − z0) + : : :
Полагая во всех этих равенствах и в исходном ряде z = z0, следовательно
b0 = f(z0), b1 |
= f0(z0); b2 = |
f00(z0) |
; : : : ; bn = |
f(n)(z0) |
, получаем bn = Cn |
|
|
n! |
|||||
|
2 |
|
|
|
||
n, т.е. указанные ряды совпадают. |
|
|
|
|||
Формула |
(2.8) называется рядом |
Тейлора. При z0 = 0 ряд (2.8) |
||||
называется рядом Маклорена. |
|
|
|
|||
37

Разложения элементарных функций в ряд Тейлора
|
ez = 1 + |
z |
|
|
|
|
z2 |
z3 |
|
|
|
zn |
|
|
||||||||||||||||||||||
|
|
+ |
|
|
|
|
+ |
|
|
|
|
+ : : : + |
|
|
+ : : : ; z C; |
|||||||||||||||||||||
|
1! |
2! |
3! |
n! |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
z3 |
|
|
|
z5 |
z7 |
z C; |
|||||||||||||||||||||
|
sin z = z − |
|
|
|
|
+ |
|
|
|
|
|
− |
|
|
+ : : : ; |
|||||||||||||||||||||
|
3! |
5! |
7! |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
z2 |
|
|
|
z4 |
z6 |
z C; |
|||||||||||||||||||||
|
cos z = 1 − |
|
|
|
|
+ |
|
|
|
|
− |
|
|
+ : : : ; |
||||||||||||||||||||||
|
2! |
|
4! |
6! |
||||||||||||||||||||||||||||||||
ln(1 + z) = z − |
|
|
z2 |
|
|
|
z3 |
− |
z4 |
|
|
|
|
|
|
|
z : |z| < 1; z C; |
|||||||||||||||||||
|
|
|
|
+ |
|
|
|
+ : : : +; |
||||||||||||||||||||||||||||
|
|
2! |
3! |
4! |
||||||||||||||||||||||||||||||||
(1 + z) = 1 + |
|
|
z + |
( − 1) |
z2 + |
( − 1)( − 2) |
z3 + : : : ; |
|||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
1! |
|
|
|
|
|
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
|
3! |
|
|||||||
1 |
|
|
|
|
|
|
|
|
|
|
z : |z| < 1; z C; |
|
|
|||||||||||||||||||||||
= 1 − z + z2 − z3 + · · · + (−1)nzn + · · · ; z : |z| < 1; z C: |
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
1 + z |
||||||||||||||||||||||||||||||||||||
38

2.4.2. Ряды Лорана
Точка z0 называется нулем функции f(z), если f(z0) = 0. В этом случае C0 = f(z0) = 0. Если же не только C0 = 0, но и
C1 = : : : = Cm−1 = 0, а Cm =6 0, то разложение функции f(z) в окрестности точки z0 имеет вид:
f(z) = Cm(z − z0)m + Cm+1(z − z0)m+1 + : : :, точка z0 называется нулем кратности m; если m = 1, то z0 называется простым нулем.
Так как Cn = f(n)(z0) , то в случае, когда z0 – ноль кратности m, n!
∑
∞
f(z0) = f0(z0) = : : := f(m−1)(z0) = 0, а значит, f(z) = Cn(z − z0)n =
n=m
= (z − z0)m'(z), где '(z) = Cm + Cm+1(z − z0) + Cm+2(z − z0)2 + : : :, при этом для функции '(z) точка z0 уже не является нулем, так как
'(z0) = Cm =6 0.
Теорема. Всякая аналитическая в кольце
r < |z − z0| < R функция f(z) может быть разложена в этом
|
|
|
∞ |
Cn(z − z0)n; |
|
|
кольце в ряд f(z) = |
(2:9) |
|||||
|
|
|
n=−∞ |
|
|
|
|
1 |
|
f( )∑ |
|
|
|
где Cn = |
|
|
d ; L – произвольная окружность |
|||
2 i |
|
n+1 |
||||
|
|
L |
( − z0) |
|
|
|
с центром в |
точке z , лежащая внутри этого кольца. |
|
||||
H |
0 |
|
|
|
||
Ряд (2.9) называется рядом Лорана. Отметим, что в
+∞ |
∞ |
|
∞ |
|
|
∑ |
∑ |
n |
∑ |
C−n |
|
|
|
n |
|
||
f(z) = n= |
−∞ |
Cn(z − z0) = n=0 Cn(z − z0) + n=1 |
(z − z0)n |
||
|
|
|
|
|
|
первая часть называется правильной частью ряда Лорана, этот ряд сходится внутри круга |z − z0| < R к аналитической функции f1(z). Вторая часть ряда Лорана называется главной частью, и она сходится вне круга |z − z0| < R к аналитической функции f2(z). Таким образом внутри кольца r < |z − z0| < R ряд (2:9) сходится к аналитической функции f(z) = f1(z) + f2(z). В частности, если функция f(z) не имеет внутри круга |z − z0| < R особых точек, то ее разложение в ряд Лорана обращается в ряд Тейлора.
39

Замечание. На практике для разложения в ряд Лорана используются уже известные разложения на интервалах аналитичности функции.
2.4.3. Классификация точек разрыва
Особая точка z = z0 функции f(z) называется изолированной, если
в некоторой ее проколотой окрестности V (z0) функция f(z) не имеет других особых точек.
Если z0 – изолированная точка функции f(z), то существует такое число R > 0, что в кольце 0 < |z − z0| < R функция аналитична
и разлагается в ряд Лорана:
∞ |
∞ |
∑ |
∑ |
f(z) = |
Cn(z − z0)n + C−n(z − z0)−n: |
n=0 |
n=1 |
Если в соответствующем ряде Лорана нет главной части, то изолированная особая точка z0 называется устранимой особой точкой
функции f(z):
Если главная часть соответствующего ряда Лорана содержит конечное число элементов, то z0 — полюс функции f(z).
Если разложение Лорана содержит в своей главной части бесконечное число членов, то точка z0 называется существенно особой точкой функции f(z).
Если z0 – устранимая особая точка, то в окрестности точки z0
∑∞
разложение Лорана имеет вид: f(z) =
n=0
справедливо в кольце 0 < |z − z0| < R, и если доопределить функцию
f(z0) = C0, где C0 = lim f(z), то точка z0 становится правильной
z→z0
точкой функции f1(z). Это, кроме всего прочего, означает, что функция f(z) ограничена в круге |z − z0| < R.
Лемма. Изолированная особая точка z = z0 является
устранимой, если существует конечный предел lim f(z) = A:
z→z0
40
