
Semenova_matem1
.pdf
1.4. Степень и корень из комплексного числа
Возведение комплексного числа z= x + iy, записанного в тригонометрической форме, т.е. z = |z|(cos '+i sin '), в степень n(n N) производится по формуле Муавра, при этом формулы бинома и геометрической прогрессии верны
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zn = |z|n(cos(n') + i sin(n')): |
|
|
|
|||||||||||||||||||||||||||||||||||||
Возведение комплексного числа z в отрицательную степень |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(−n) (n N) также производится по формуле Муавра: |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z(−n) |
= |
|
|
|
|
1 |
|
|
|
(cos(n') − i sin(n')): |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|z|n |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
Извлечение корня степени m(m N) комплексного числа z = x + iy, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
записанного в тригонометрической форме, т.е. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = |z|(cos ' + i sin '); |
|
|
|
||||||||||||||||||||||||||||||||
дает m различных корней: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
' + 2 k |
|
|
|
|
|
|
|
' + 2 k |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
wk+1 = |
√|z|(cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ i sin |
|
|
|
|
|
|
|
|
|
|
|
); k = 0; 1; 2; :::; (m − 1): |
(1:3) |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
m |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Замечание. Все m корней w1; :::; wm лежат в вершинах правильного |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
m – угольника с центром в начале координат. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Пример 2. |
|
Решить уравнение z3 = −27i: |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
B Перепишем |
|
|
уравнение |
|
|
|
в виде z |
|
|
|
|
|
|
= √3 |
|
. Запишем число |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
−27i |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
w = |
|
|
27i в тригонометрической форме (1.1). Видим, что x = 0; y = |
27 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
cos ' = |
0 |
= 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
− |
||||||||||||||||||||||||||||||
|
w |
|
|
= 27, ' : |
|
|
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
sin ' = |
−27 |
= |
1; |
|
|
|
|
|
|
' = 2 , |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
| |
|
|
| |
|
|
|
|
|
{ |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 27 |
|
|
|
|
|
|
−3 |
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
в результате w = 27(cos 2 |
|
+ i sin 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
Тогда при k = 0: z1 = √3 |
|
|
|
|
|
|
|
|
|
|
0+ 32 |
|
|
|
|
|
|
|
0+ 32 |
) = 3(cos |
+ i sin ) = |
|||||||||||||||||||||||||||||||||||||||||||
27(cos |
+ i sin |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|||||||||
= 3(0 + i) = 3i; |
√3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
при k = 1: z2 = |
|
|
2 + |
|
|
|
+ i sin |
2 + |
|
) = 3(cos 7 + i sin 7 ) = |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
27(cos |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
6 |
|
6 |
|
|
|||||||||||||||||
= 3(− |
3 |
− |
i |
) = − |
3 2 |
3 − 32i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
2 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
при k = 2 : z3 = |
√3 27(cos |
4 + |
2 |
|
|
|
|
+ i sin |
4 + |
|
2 |
|
) = 3(cos 11 |
+ i sin |
11 ) = |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
√ |
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
6 |
|
6 |
|
|||||||||||||||||||
= 3( 23 − 2i ) = 3 2 3 − 32i :
11
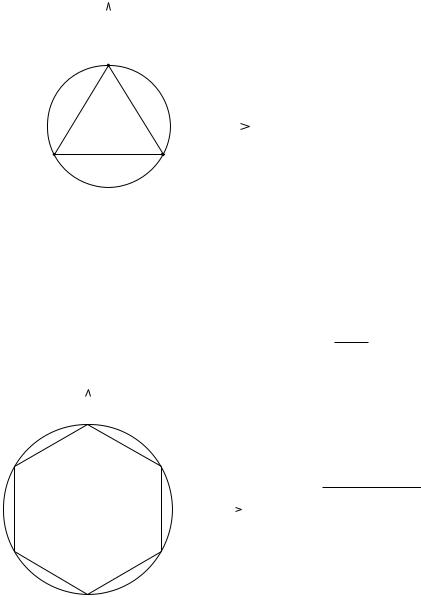
|
|
|
IM Z |
|
|
|
Данную задачу можно |
проиллю- |
||||||||
|
|
|
|
|
|
стрировать |
графически |
(рис.1.7). |
||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
Z1 |
|
|
|
Построим окружность с центром |
|||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
в начале координат и радиусом рав- |
|||||||||
|
|
|
|
|
|
|
ным |
|
|
|
= √3 |
|
= 3, |
тогда по- |
||
|
|
|
|
|
|
|
3 |z| |
27 |
||||||||
|
|
|
|
|
|
|
лученные значения являются вер- |
|||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
0 |
|
3 |
RE Z |
|
√ |
|
|
|
|
|
|
||
|
|
|
Z2 |
|
Z 3 |
|
шинами вписанного в окружность |
|||||||||
|
|
|
|
|
|
|
правильного треугольника. Первая |
|||||||||
|
|
|
|
|
|
|
вершина вписанного треугольника |
|||||||||
|
|
|
|
|
|
|
соответствует наименьшему значе- |
|||||||||
' = |
|
Рис. 1.7 |
|
|
нию аргумента: |
|
|
. J |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3 |
= , остальные вершины получаем, добавляя каждый раз |
2 |
||||||||||||||
2·3 |
|
|||||||||||||||
n |
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|||
√
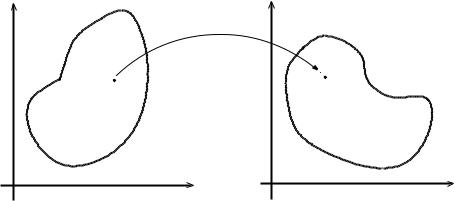
Пример 3. Найти все значения корня 6 −64:
|
|
|
IM Z |
Z1 |
|
|
Z6 |
|
Z2 |
|
|
|
|
|
|
|
2 |
0 |
2 RE Z |
|
|
|||
|
|
Z5 |
|
Z |
|
|
|
|
3 |
|
|
|
|
Z 4 |
|
|
|
|
|
Рис. 1.8
B Запишем число z = −64 в тригонометрической форме (1.1). Для этого найдем значения модуля и аргумента
|z| = |
|
(−64)2 + 02 = 64, |
|
|||||||||
|
√cos ' = |
x |
= −6464 = −1; |
|
||||||||
' : |
|z| |
|
||||||||||
' = {: sin ' = |
y |
= |
0 |
= 0; |
|
|||||||
|z| |
64 |
|||||||||||
Тогда, при k = 0 : |
|
|||||||||||
|
√6 |
|
|
|
|
|
||||||
z = |
64(cos 0+ + i sin 0+ ) = |
|
||||||||||
1 |
6 |
6 |
|
|||||||||
= 2(cos + i sin |
) = √ |
|
+ i; |
|
||||||||
3 |
|
|||||||||||
|
6 |
|
|
|
6 |
|
|
|
|
|
||
при k = 1 : z2 = |
√6 |
|
|
2 + + i sin +2 ) = 2(cos |
+ i sin ) = |
||
64(cos |
|||||||
|
|
|
|
6 |
6 |
2 |
2 |
= 2i; |
√6 |
|
|
|
|
|
|
||
при k = 2 : z3 = |
|
|
+4 + i sin +4 ) = 2(cos |
5 + i sin 5 |
|||||
64(cos |
|||||||||
√ |
|
+ i; |
|
|
|
6 |
6 |
6 |
6 |
= − |
3 |
√6 |
|
|
|
|
|
|
|
при k = 3 : z4 = |
|
|
+6 + i sin +6 ) = 2(cos |
7 + i sin 7 |
|||||
64(cos |
|||||||||
√ |
|
|
|
|
|
6 |
6 |
6 |
6 |
= − 3 − i; |
√6 |
|
|
|
|
|
|
||
при k = 4 : z5 = |
64(cos |
+8 + i sin +8 ) = 2(cos |
3 + i sin 3 |
||||||
|
|
|
|
|
|
6 |
6 |
2 |
2 |
= −2i;
) =
) =
) =
12
при k = 5 : z3 = √6 |
|
|
|
|
|
|
|
|
|
|
|||||||
64(cos +10 + i sin +10 ) = |
|
|
|
|
|
||||||||||||
6 |
6 |
|
|
|
|
|
|
|
|
||||||||
|
11 |
|
11 |
) = √ |
|
− i. |
|
|
|
|
|
|
|
|
|
||
= 2(cos |
+ i sin |
3 |
|
|
|
|
|
|
|
|
|
||||||
6 |
6 |
|
|
|
|
|
|
|
|
|
|||||||
Полученные значения изображаются вершинами правильного шести- |
|||||||||||||||||
угольника, вписанного в окружность радиуса |
6 |
|
|
|
|
√6 |
|
= 2 с центром |
|||||||||
|
z |
|
= |
64 |
|||||||||||||
в начале координат (рис. 1.8). J |
|
√| |
|
| |
|
|
|
|
|||||||||
13
Глава 2.
Элементы теории функции комплексного переменного
2.1.Функция комплексного переменного
2.1.1.Основные понятия
Рассмотрим два множества D и E R2, элементами которых являются комплексные числа.
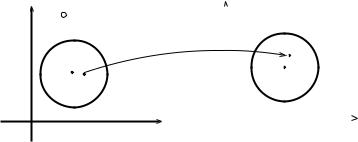
Пусть z = x+iy D, w = u+iv E — точки комплексной плоскости. Если каждому комплексному числу z D поставлено в соответствие определенное комплексное число w E, то говорят, что на множестве
D определена однозначная функция комплексного переменного w = f(z), отображающая множество D на множество E. Если же каждому значению z D соответствует несколько значений w , то функция w = f(z) называется многозначной (рис. 2.1).
Y |
F |
V |
|
Z |
|
|
W |
D |
|
|
|
|
|
|
E |
0 |
X |
0 |
U |
|
Рис. 2.1 |
|
|
14
Множество D называется областью определения функции
w = f(z); множество E1 E всех значений, которые принимает функция f(z), называется областью значений.
Функцию w = f(z) можно представить в виде f(x + iy) =
= u(x; y) + iv(x; y), где u = u(x; y) = Ref(z); v = v(x; y) = Imf(z). Таким образом, задание функции комплексного переменного равносильно заданию двух функций двух действительных переменных.
2.1.2. Предел и непрерывность
Окрестностью V (z0) точки z0 называется внутренность круга радиусом с центром в точке z0, то есть все точки, удовлетворяющие условию
z : |z − z0| < . Проколотой окрестностью V (z0) точки z0 называются точки, удовлетворяющие условию z : 0 < |z−z0| < , то есть внутренность круга радиусом с центром в точке z0, за исключением самой точки z0.
Пусть однозначная функция w = f(z) определена в некоторой
проколотой окрестности V (z0) точки z0. Число A называется пределом
функции w = f(z) в точке z0 (или при z → z0), если для любого положительного числа " > 0 найдется такое положительное число , что для всех z, удовлетворяющих неравенству 0 < |z − z0| < , выполняется неравенство |f(z) − A| < ", т.е.
(" > 0) ( > 0); (z V (z0))[f(z) V (A)]:
Y V(Z0)
Z0
0 |
X |
Рис. 2.2
lim
x ! x0 y ! y0
|
V |
|
|
Пишут |
lim f(z) |
= |
A |
||
|
|
|
|
||||||
F |
|
V(A) |
(рис.2.2). |
z→z0 |
определения |
||||
|
|
|
|
Из |
|||||
|
|
A |
|
предела |
|
|
функции |
||
|
|
|
|
комплексного |
переменного |
||||
|
|
|
|
|
следует, |
|
что |
|
если |
0 |
|
U |
|
|
|
||||
|
|
lim f(z) |
= |
w0, |
то |
||||
|
|
|
|
||||||
|
|
|
|
|
|||||
|
|
|
|
z→z0 |
|
|
|
|
|
|
|
|
|
существуют пределы |
|
||||
u(x; y) = u0; |
lim |
v(x; y) = v0: |
|
|
(2:1) |
||||
|
|
|
x ! x0 |
|
|
|
|
|
|
y ! y0
И наоборот, если существуют пределы (2.1), то существует и предел
lim f(z) = w0.
z→z0
15

Свойства функций комплексного переменного, имеющих предел:
1◦ |
если функция комплексного переменного w = f(z) имеет предел |
|||||||||
|
в точке z0, то он единственный; |
|
|
|
|
|
||||
2◦ |
пусть функции f(z) и g(z) имеют конечные пределы при z → z0, |
|||||||||
|
тогда: |
|
|
|
|
|
|
|
|
|
|
lim (c1f(z) + c2g(z)) = c1 |
lim f(z) + c2 |
lim g(z); где c1; c2 = const; |
|||||||
|
z→z0 |
|
|
|
z→z0 |
z→z0 |
|
|
||
|
lim (f |
(z) · |
lim f(z) |
· |
lim g(z); |
|||||
|
z |
→ |
z0 |
g(z)) = z z0 |
|
z |
→ |
z0 |
||
|
|
|
|
→ |
|
|
|
|
||
lim f(z) =
z→z0 g(z)
lim f(z)
z→z0 |
|
если |
|
|
; |
V (z0) : g(z) 6= 0: |
|
lim g(z) |
|||
z→z0 |
|
|
|
Пусть функция w = f(z) определена в некоторой окрестности V (z0)
точки z0. Функция w = f(z) называется непрерывной в точке z0, если lim f(z) = f(z0).
Функция w = f(z) непрерывна в точке z0, если бесконечно малому приращению аргумента z соответствует бесконечно малое приращение
функции f, то есть lim f(z) = 0.
Замечание. Модуль непрерывной функции комплексного переменного |f(z)| обладает теми же свойствами, что и непрерывная функция действительного переменного. Действительно, если lim f(z) = 0, то
lim |
u(z) = 0 и lim |
|
v(z) = 0, следовательно, |
|||||
x ! 0 |
|
x ! 0 |
|
|
|
|
|
|
y ! 0 |
|
y ! 0 |
√ |
|
|
|
|
= 0, что и означает, что функция |
lim |
| f(z)| = |
lim |
u |
2 |
+ v |
2 |
||
x ! 0 |
x ! 0 |
|
|
|
||||
y ! 0 |
|
y ! 0 |
|
|
|
|
|
|
|f(z)| является непрерывной функцией двух переменных. Функция w = f(z) называется непрерывной на множестве D; если она непрерывна в каждой точке этого множества.
2.1.3. Элементарные функции комплексного переменного
Показательная функция w = ez z C определяется формулой
w = ez = ex(cos y + i sin y):
16
Легко убедиться, что при z R (z = x+ iy) показательная функция комплексного переменного совпадает с показательной функцией действительного переменного.
Свойства показательной функции:
1◦
2◦
3◦
ez1 · ez2 = ez1+z2 , z1; z2 C;
(ez)n = ezn, где n N; z C;
w = ez ни в одной точке в ноль не обращается, т.е. ez =6 0 z C:
Действительно, |ez| = |ex(cos y + i sin y)| = |ex| = ex =6 0 x R;
4◦ |
lim ez = 0 |
lim ez = |
∞ |
: |
||
|
Re z |
→−∞ |
, Re z + |
|
|
|
|
|
→ ∞ |
|
|
|
|
|
Замечание. Выражение |
lim ez не имеет смысла; |
||||
|
|
|
|
z→∞ |
|
|
5◦ |
показательная функция w = ez является периодической с периодом |
|||||
|
T = 2 i. |
|
|
|
|
|
Действительно, при n N, ez+nT = ez+n2 i = ez · en2 i = = eze0(cos(2 n) + i sin(2 n)) = ez:
Замечание. Показательная функция w = ez (−∞; 0) (0; ∞).
Число w называется логарифмом числа z =6 0, если ew = z, и обозначается w = Lnz.
Значение показательной функции ew = z всегда отлично от нуля при z 6= 0, значит, функция w = Ln z определена на всей плоскости z C.
Легко заметить, что Ln z = ln |z|+ i(arg z + 2 k). Кроме того, из этой формулы следует , что w = Ln z — многозначная функция. При k = 0
получаем однозначную функцию, которую называют главным значением
логарифма и обозначают ln z, т.е. Ln z = ln z + 2 ki:
Свойства логарифма:
1◦ Ln (z1 · z2) = Ln z1 + Ln z2; 2◦ Ln zn = nLn z; n N:
Если n — натуральное число, то степенная функция определяется равенством w = zn = rn(cos n' + i sin n'), где r = |z|; ' = arg z. Функция w = zn — однозначная.
17

Если n = 1q , где q N, то извлечение корня определяется равенством
1 |
|
|
|
+ 2 k |
|
arg z + 2 k |
|
= √q |
|
|
|
||||
w = z q |
|z|(cos |
arg z |
+ i sin |
|
); |
||
q |
q |
||||||
1
где k = 0; 1; 2; 3; :::; q − 1. Функция w = eq — многозначная функция.
Степенная функция w = za с произвольным показательным аргументом a = + i — многозначная функция и определяется равенством
w = za = eaLnz:
Тригонометрические функции комплексного переменного z определяются равенствами:
sin z = |
eiz − e−iz |
; cos z = |
eiz + e−iz |
; tg z = |
sin z |
; ctg z = |
cos z |
: |
|
2i |
2 |
cos z |
sin z |
||||||
|
|
|
|
|
Легко убедиться, что при действительных z эти функции превращаются в тригономметрические функции действительного переменного.
Свойства тригонометрических функций:
1◦ |
sin2 z + cos2 z = 1; |
|
|
|
|
|
|
|
|
||||
2◦ |
sin 2z = 2 sin z cos z; |
|
cos 2z = cos2 z − sin2 z; |
|
|
|
|||||||
3◦ |
cos(z1 ± z2) = cos z1 cos z2 sin z1 sin z2, и т.д.; |
|
|
|
|||||||||
4◦ |
sin(z + 2 n) = sin z; cos(z + 2 n) = cos z; tg(z + n) = tg z |
n |
N |
; |
|||||||||
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
5◦ |
cos( |
− |
z) = cos z; sin( |
− |
z) = |
− |
sin z; |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
6◦ |
cos z = 0 при z = 2 + k ; |
k N; |
|
|
|
||||||||
7◦ |
lim |
sin z = |
∞ |
; |
|
lim cos z = : |
|
|
|
||||
|
Im z |
→±∞ |
|
|
|
Im z |
|
∞ |
|
|
|
||
|
|
|
|
|
|
|
→±∞ |
|
|
|
|||
Гиперболические функции комплексного переменного определяются равенствами
sh z = |
ez − e−z |
; |
ch z = |
ez + e−z |
; |
th z = |
sh z |
; |
cth z = |
ch z |
: |
|
|
ch z |
sh z |
||||||||
2 |
|
2 |
|
|
|
|
|
||||
18
Замечание.
sh iz = i sin z; т.е. sin z = −i sh iz; ch iz = cos z:
Свойства гиперболических функций:
1◦ |
ch2 z |
− |
sh2 z = 1 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2◦ ch 2z = sh2 z + ch2 z; sh 2z = 2 ch z sh z; |
|
|||||||||
3◦ |
ch(z1 + z2) = ch z1 ch z2 + sh z1 sh z2 и т.д.; |
|
||||||||
4◦ sh z + ch z = ez; |
|
|
|
|
|
|
|
|||
5◦ |
ch( |
z) = ch z; |
sh( |
− |
z) = |
− |
sh z |
; |
|
|
|
− |
|
|
|
|
|
|
|||
6◦ |
sh(z + 2 in) = sh z; ch(z + 2 in) = ch z; th(z + in) = th z; n |
: |
||||||||
|
|
|
|
|
|
|
|
|
N |
|
Обратные функции. Число w называется арксинусом числа z, если sin w = z и обозначается w = Arcsin z. Остальные определения даются
аналогично: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Arcsin z = −iLn (iz + √ |
|
|
); |
||||||||||||||
12− z2 |
|||||||||||||||||
Arccos z = −i iLn i(z |
z |
√ |
|
|
|
|
|
||||||||||
z |
− |
1); |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
+ |
|
||||||
Arctg |
z = |
|
|
|
|
Ln |
|
− |
; |
z = |
|
|
i; |
||||
|
|
− |
2 |
i + z |
|
|
6 ± |
||||||||||
|
|
z = i |
z − i |
; |
z = |
|
|
i: |
|||||||||
Arcctg |
|
|
|
Ln |
|
|
|
|
6 ± |
|
|||||||
|
|
2 |
z + i |
|
|
|
|||||||||||
Функции, обратные гиперболическим, обозначаются соответственно w = Arsh z (ареасинус), w = Arсh z (ареакосинус), w = Arth z
(ареатангенс), w = Arсth z (ареакотангенс) Для обратных гиперболиче-
ских функций справедливы формулы:
Arsh z = Ln (z + |
√ |
|
|
); |
|||||||||
1 + z2 |
|||||||||||||
Arch z = Ln (z + |
|
|
|
|
|
|
|||||||
|
|
|
z2 − 1); |
||||||||||
|
1 |
|
|
|
1 + z |
|
|
|
|
|
|||
Arth z = |
Ln |
√ |
; |
|
|
|
|||||||
2 |
|
1 − z |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||
Arcth z = |
|
1 |
Ln |
|
z + 1 |
|
: |
|
|
||||
2 |
|
z − 1 |
|
|
|||||||||
|
|
|
|
|
|
|
|||||||
Все вышеперечисленные функции многозначные.
19

2.2.Дифференцирование функции комплексного переменного
2.2.1.Условия Коши – Римана
Пусть однозначная функция w = f(z) определена в некоторой окрестности V (z) точки z. Тогда предел
lim |
w |
= lim |
f(z + z) − f(z) |
= f0(z); |
|
z |
z |
||||
z→0 |
z→0 |
|
если он существует, называется производной функции f(z) в точке z, а сама функция называется дифференцируемой в точке z.
Замечание. Из дифференцируемости функции f(z) в некотрой точке z следует непрерывность функции в этой точке. Обратное неверно.
Теорема. Если функция w = f(z) = u(x; y) + iv(x; y)
определена в некоторой окрестности V (z) точки z, причем
в этой окрестности действительные функции u(x; y); v(x; y)
дифференцируемы, то для дифференцируемости функции w = f(z) необходимо и достаточно, чтобы выполнялись условия
Коши — Римана: |
@v |
|
|
||||||
@u |
= |
@v |
; |
@u |
= − |
: |
(2:2) |
||
|
@x |
@y |
@y |
@x |
|||||
С учетом условий Коши – Римана, производную дифференцируемой функции f(z) можно находить по одной из формул:
f0(z) = @u@x + i@x@v ; f0(z) = @u@x − i@u@y ; f0(z) = @y@v + i@x@v ; f0(z) = @y@v − i@u@y :
Свойства дифференцируемых функций:
1◦ пусть f1(z), f2(z) дифференцируемы в некоторой точке z, тогда:
(f1(z) ± f2(z))0 = f10 (z) ± f20 (z);
(f1(z) · f2(z))0 = f10(z) · f2(z) + f1(z) · f20 (z);
20
