кр №1

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ОРЛОВСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ ДИСТАНЦИОННОГО ОБУЧЕНИЯ

КОНТРОЛЬНАЯ РАБОТА

по дисциплине "Математика"

Вариант № 4

Работу выполнил(а) студент(ка) Выгорчук Виктория Александровна группа 1-1Мн/с ФДО г. Орел №121394	Замечания по работе
Работу проверил(а) Ноздрунов Владимир Васильевич 1 семестр

Отметка о зачете __________________ дата "____" _________20 г.

Подпись преподавателя ________________

г. Орел, 2012 г.

Задание 1. Вычислить определитель

_{Решение:}

_{Вычислим определитель: а) разложив его по элементам i-ой строки; б) разложив его по элементам j-го столбца.}

_{i = 1, j = 2}

_{а). Вычисляем определитель, разложив его по элементам первой строки:}

_{б) Вычисляем определитель, разложив его по элементам второго столбца:}

_Ответ:

Задание 2. Дана матрица A. Найти: а) ; б) _.

Решение:

Обратная матрица матрицы А имеет вид

,

где det А = ,

т.е. матрица A - невырожденная, и, значит, существует матрица .

Найдем алгебраические дополнения к элементам матрицы А:

, , ,

, , ,

, , .

Тогда обратная матрица

;

Найдем произведение матрицы A и

Ответ: а) , б)

Задание 3. Проверить совместность линейной системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) методом Гаусса.

_{Решение: Совместность данной системы проверим по теореме Кронекера - Капелли. С помощью элементарных преобразований найдем ранг матрицы}

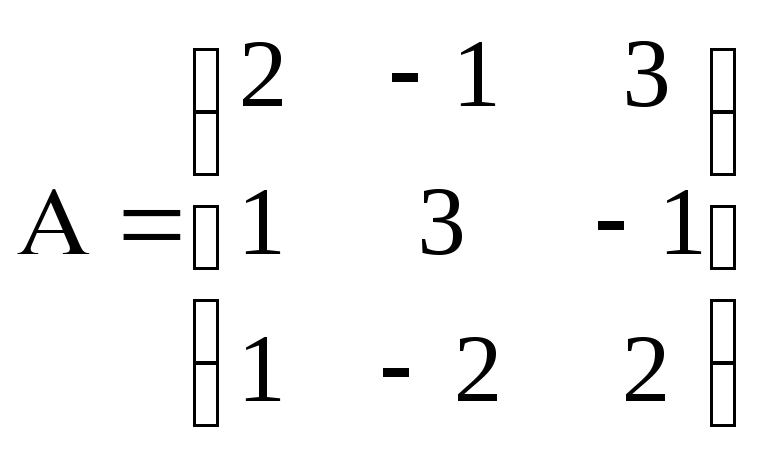
данной системы и ранг расширенной матрицы

Исследуем эту систему по теореме Кронекера-Капелли.

Умножим 2-ую строку на (-2). Добавим 2-ую строку к 1-ой:

Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:

Умножим 1-ую строку на (5). Умножим 2-ую строку на (7). Добавим 2-ую строку к 1-ой:

Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля, причем этот минор принадлежит как основной матрице, так и расширенной, следовательно rang(A) = rang(B) = 3. Поскольку ранг основной матрицы равен рангу расширенной, то система является совместной.

Найдем решение системы по формулам Крамера

,

где определитель системы , составленный из коэффициентов уравнений системы при неизвестных,

,

и определители , полученные из определителя заменой первого, второго и третьего столбцов соответственно на столбик свободных членов

Решим систему методом Гаусса. Решать будем в два этапа. На первом этапе (прямой ход) система приводится к ступенчатому виду, путем последовательного исключения переменных. На втором этапе решения (обратный ход) мы будем последовательно находить переменные из получившейся ступенчатой системы.

Исключим переменную x1 из всех уравнений, за исключением первого. Поменяем местами уравнения 1 и 2, умножим коэффициенты уравнения 1 на (-2), прибавим получившееся уравнение к уравнению 2, умножим коэффициенты уравнения 1 на (-1), прибавим получившееся уравнение к уравнению 3, исключим переменную x2 из последнего уравнения, умножим коэффициенты уравнения 2 на 5 и умножим коэффициенты уравнения 3 на (-7). Прибавим уравнение 2 к уравнению 3.

Из полученной системы применяя "обратный ход" находим

, ,

Ответ: , ,

Задание 4. Решить однородную систему линейных алгебраических уравнений.

_{Решение:}

Определитель системы

поэтому система имеет единственное нулевое решение:

Ответ: .

Задание 5. Даны векторы _.

Необходимо: а) вычислить смешанное произведение трех векторов a, -2b, -7c; б) найти модуль векторного произведения векторов 4b, 3c; в) вычислить скалярное произведение двух векторов 2a, -7c; г) проверить, будут ли коллинеарными или ортогональными два вектора b, c; д) проверить, будут ли компланарны три вектора 2a, 4b, 3c.

Решение:

а) Так как -2b = -4i+12j, -7c=-7i+21j-14k, то

a (-2b)(-7c)=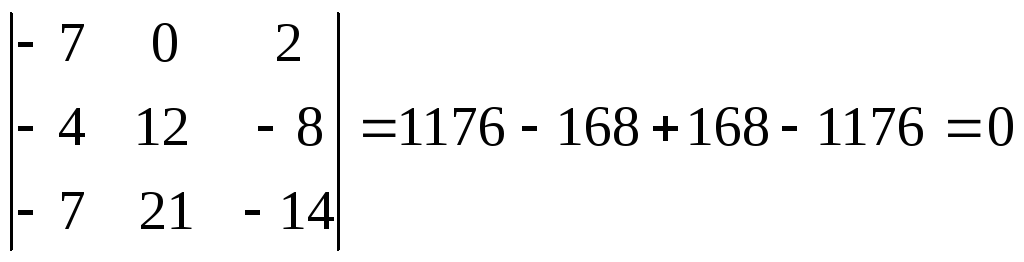

б) Поскольку 4b=8i-24j+16k, 3c=3i-9j+6k,то

3c4b=

в) Находим 2a= -14i+4k, -7c= -7i+21j-14k

2a(-7c)=-14(-7)+021+4(-14)=98-56=42

г) Так как b=(2, -6, 4), с=(1, -3, 2) и , то векторы b и с коллинеарны. Поскольку bс = , то векторы b и с не ортогональны.

д) Находим 2а= -14i+4k, 4b= 8i-24j+16k, 3c= 3i-9j+6k.

Векторы 2a, 4b, 3c компланарны, если их смешанное произведение равно нулю, т.е. . Вычисляем:

Т.е. векторы 2a, 4b, 3c компланарны.

Ответ: а) a(-2b)(-7c)=0, б) , в)2a(-7c)=42, г) векторы b и с коллинеарны и не ортогональны, д) векторы 2a, 4b, 3c компланарны.

Задание 6. Даны вершины треугольника . Найти:

а) уравнение стороны АВ;

б) уравнение высоты СН;

в) уравнение медианы АМ;

г) точку N пересечения медианы AM и высоты СН;

д) уравнение прямой, проходящей через вершину C параллельно стороне AB;

е) расстояние от точки C до прямой AB.

Построить все точки и линии, данные в задаче и полученные в ходе решения задачи.

Решение:

а) Воспользовавшись уравнением прямой, проходящей через две точки

,

получим уравнение стороны АВ:

Откуда

или

б) Используя уравнение прямой

найдем угловой коэффициент прямой АВ

Тогда . С учетом условия перпендикулярности прямых АВ и СН () угловой коэффициент высоты СН: .

Используя уравнение прямой проходящее через точку с угловым коэффициентом

составим уравнение высоты СН. По точке С(9, 5) и угловому коэффициенту составляем уравнение высоты СН :

или .

в) По формулам координат середины отрезка

находим координаты х, у середины М отрезка ВС:

.

Теперь по двум известным точкам A и М составляем уравнение медианы AM:

или .

г) Для нахождения координат точки N пересечения медианы AM и высоты СН составляем систему уравнений

Решая ее, получаем ;

д) Так как прямая, проходящая через вершину С, параллельна стороне АВ, то их угловые коэффициенты равны. Тогда, согласно уравнению

,

по точке С и угловому коэффициенту составляем уравнение прямой CD:

или .

е) Расстояние от точки С до прямой АВ вычисляем по формуле:

_Тогда

Ответ: а) ,

б) _,

_{в) ,}

_{г) ,}

_{д) ,}

_е)

Задание 7. Составить канонические уравнения: а) эллипса; б) гиперболы; в) параболы (А, В - точки, лежащие на кривой, F - фокус, a - большая (действительная) полуось, b - малая (мнимая) полуось, - эксцентриситет, - уравнение асимптот гиперболы, D - директриса кривой, 2c - фокусное расстояние), если

а) . , A(-5, 0) б) . ; в). D: y = 1.

Решение:

а) Каноническое уравнение эллипса имеет вид

,

По условию задачи большая полуось . Для эллипса выполняется равенство . Подставив в него значения и , найдем . Тогда искомое уравнение эллипса

б) Каноническое уравнение гиперболы имеет вид

По условию мнимая полуось . Для гиперболы справедливо равенство . Поэтому . Записываем искомое уравнение гиперболы:

в) Каноническое уравнение параболы в данном случае должно иметь вид

,

а уравнение ее директрисы . Но по условию задачи уравнение директрисы . Поэтому искомое каноническое уравнение параболы имеет вид

_{Ответ: а) , б) , в)}