
- •Нижнекамский химико-технологический институт (филиал)
- •2 Вопросы для самоконтроля
- •3 Рекомендуемая литература
- •4 Основные понятия, примеры решения задач и контрольные задания
- •4.1 Значащие цифры и правила округления
- •4.2 Обработка результатов анализа методами математической статистики.
- •4.3 Линейный метод наименьших квадратов
- •Тема 4.4 Линейная корреляция и коэффициент корреляции
- •4.5 Проверка нормальности распределения результатов химического анализа.
- •4.6 Предел обнаружения
4.2 Обработка результатов анализа методами математической статистики.
Рассмотрим некоторые понятия и основные подходы к классификации погрешностей. По способу вычисления погрешности можно подразделить на абсолютные и относительные.
Абсолютная погрешность равна разности среднего измерения величины х и истинного значения этой величины:
![]()
В отдельных случаях, если это необходимо, рассчитывают погрешности единичных определений:
![]()
Заметим, что измеренной величиной в химическом анализе может быть как содержание компонента, так и аналитический сигнал. В зависимости от того, завышает или занижает погрешность результат анализа, погрешности могут быть положительные и отрицательные.
Относительная погрешность может быть выражена в долях или процентах и обычно знака не имеет:
![]() или
или
![]()
Можно классифицировать погрешности по источникам их происхождения. Так как источников погрешностей чрезвычайно много, то их классификация не может быть однозначной.
Чаще всего погрешности классифицируют по характеру причин, их вызывающих. При этом погрешности делят на систематические и случайные, выделяют также промахи (или грубые погрешности).
К систематическим относят погрешности, которые вызваны постоянно действующей причиной, постоянны во всех измерениях или меняются по постоянно действующему закону, могут быть выявлены и устранены.
Случайные погрешности, причины появления которых неизвестны, могут быть оценены методами математической статистики.
Промах — это погрешность, резко искажающая результат анализа и обычно легко обнаруживаемая, вызванная, как правило, небрежностью или некомпетентностью аналитика. На рис. 1.1 представлена схема, поясняющая понятия систематических и погрешностей и промахов. Прямая 1 отвечает тому идеальному случаю, когда во всех N определениях отсутствуют систематические и случайные погрешности. Линии 2 и 3 тоже идеализированные примеры химического анализа. В одном случае (прямая 2) полностью отсутствуют случайные погрешности, но все N определений имеют постоянную отрицательную систематическую погрешность Δх ; в другом случае (линия 3) полностью отсутствует систематическая погрешность. Реальную ситуацию отражает линия 4:имеются как случайные, так и систематические погрешности.
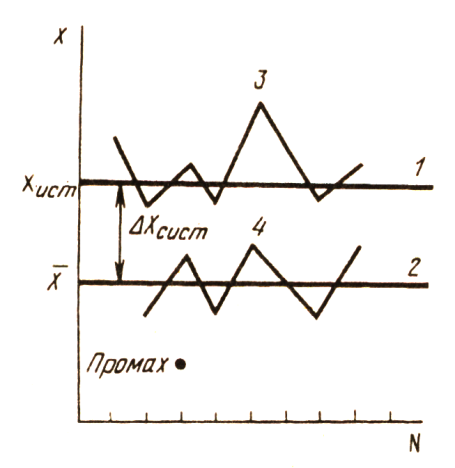
Рис. 4.2.1 Систематические и случайные погрешности химического анализа.
Деление погрешностей на систематические и случайные в известной степени условно.
Систематические погрешности одной выборки результатов при рассмотрении большего числа данных могут переходить в случайные. Например, систематическая погрешность, обусловленная неправильными показаниями прибора, при измерении аналитического сигнала на разных приборах в разных лабораториях переходит в случайную.
Воспроизводимость характеризует степень близости друг к другу единичных определений, рассеяние единичных результатов относительно среднего (рис. 1.2).
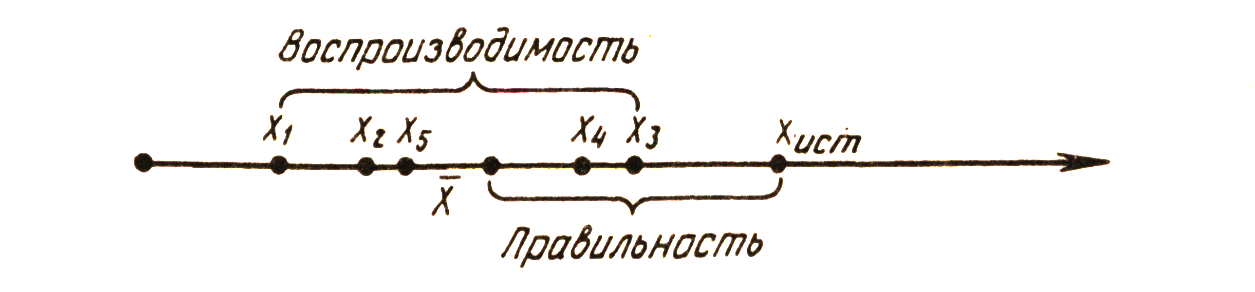
Рис. 4.2..2. Воспроизводимость и правильность химического анализа
В отдельных случаях наряду с термином «воспроизводимость» используют термин «сходимость». При этом под сходимостью понимают рассеяние результатов параллельных определений, а под воспроизводимостью — рассеяние результатов, полученных разными методами, в разных лабораториях, в разное время и т. п.
Правильность — это качество химического анализа, отражающее близость к нулю систематической погрешности. Правильность характеризует отклонение полученного результата анализа от истинного значения измеряемой величины (см. рис.1.2).
Генеральная совокупность — гипотетическая совокупность всех мыслимых результатов от -∞ до +∞;
Анализ
экспериментальных данных показывает,
что большие по значению погрешности
наблюдаются реже,
чем малые. Отмечается также, что при
увеличении числа наблюдений одинаковые
погрешности разного знака встречаются
одинаково
часто. Эти и другие свойства случайных
погрешностей описываются нормальным
распределением или уравнением
Гаусса, которое
описывает плотность вероятности ![]() .
.
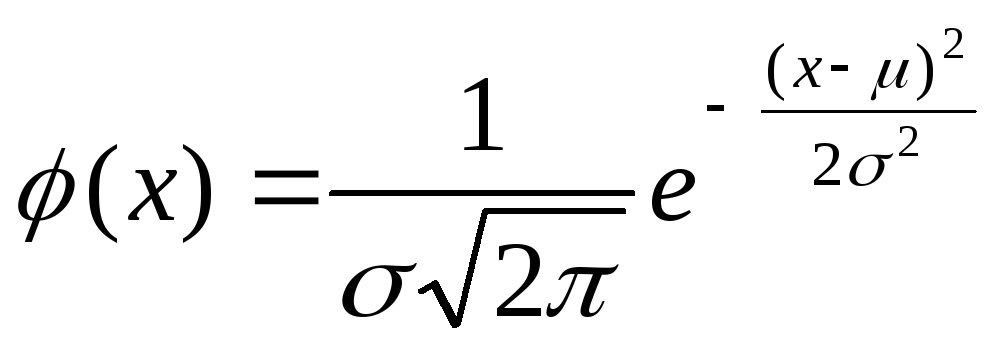
![]()
где х-значение случайной величины;
μ – генеральное среднее (математическое ожидание-постоянный параметр);
Математическое
ожидание -
для
непрерывной случайной величины
представляет собой предел, к которому
стремится среднее
![]() при неограниченном увеличении выборки.
Таким образом, математическое ожидание
является средним значением для всей
генеральной совокупности в целом, иногда
его называют
генеральным
средним.
при неограниченном увеличении выборки.
Таким образом, математическое ожидание
является средним значением для всей
генеральной совокупности в целом, иногда
его называют
генеральным
средним.
σ2 —дисперсия (постоянный параметр) - характеризует рассеяние случайной величины относительно своего математического ожидания;
σ – стандартное отклонение.
Дисперсия – характеризует рассеяние случайной величины относительно своего математического ожидания.
Выборочная совокупность (выборка) — реальное число (n) результатов, которое имеет исследователь , n = 3 ÷ 10.
Нормальный закон распределения неприемлем для обработки малого числа изменений выборочной совокупности (обычно 3 – 10) – даже если генеральная совокупность в целом распределена нормально. Для малых выборок вместо нормального распределения используют распределение Стьюдента (t – распределение), которое связывает между собой три основные характеристики выборочной совокупности –
-ширину доверительного интервала;
-соответствующую ему вероятность;
- объем выборочной совокупности.
Перед обработкой данных с применением методов математической статистики необходимо выявить промахи (грубые ошибки) и исключить их из числа рассматриваемых результатов. Одним из наиболее простых является метод выявления промахов с применением Q – критерия с числом измерений n < 10:
![]()
где R = хмакс - хмин – размах варьирования; х1 – подозрительно выделяющееся значение; х2 – результат единичного определения, ближайший по значению к х1.
Полученное значение сравнивают с критическим значением Qкрит при доверительной вероятности Р = 0,95. Если Q > Qкрит, выпадающий результат является промахом и его отбрасывают.
Основные
характеристики выборочной совокупности.
Для выборки из n
результатов
рассчитывают среднее,
![]() :
:
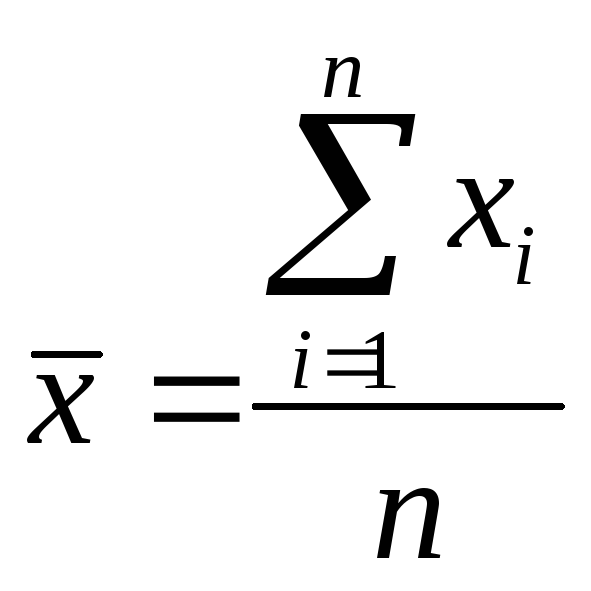
и дисперсию, характеризующую рассеяние результатов относительно среднего:
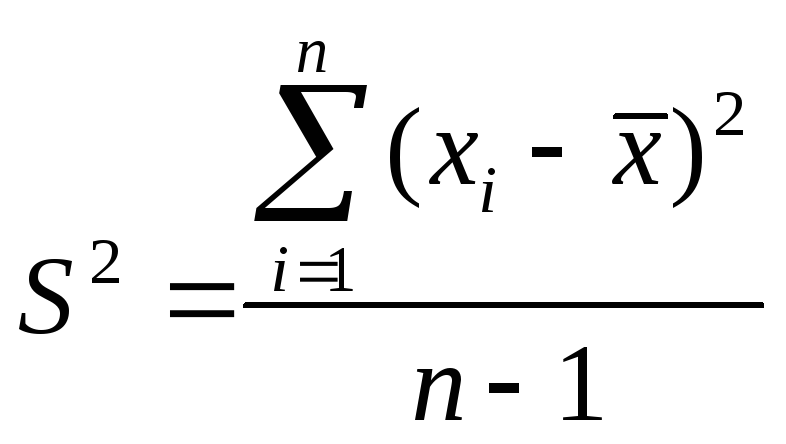
Дисперсия в явном виде не может быть использована для количественной характеристики рассеяния результатов, поскольку ее размерность не совпадает с размерностью результата анализа. Для характеристики рассеяния используют стандартное отклонение, S.
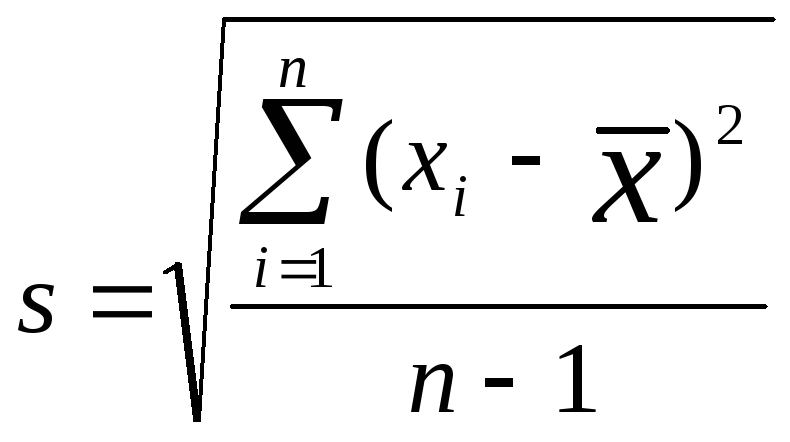
Эту величину называют также средним квадратичным (или квадратическим) отклонением или средней квадратичной погрешностью отдельного результата.
Относительное стандартное отклонение или коэффициент вариации (V) вычисляют по соотношению
![]()
Дисперсию среднего арифметического вычисляют:
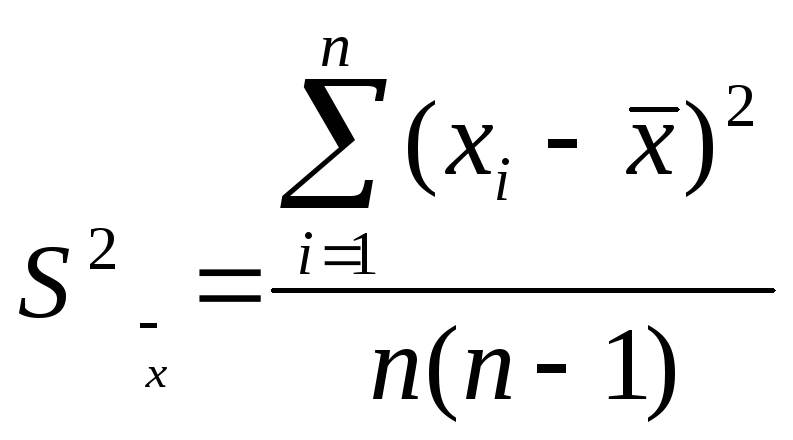
и стандартное отклонение среднего
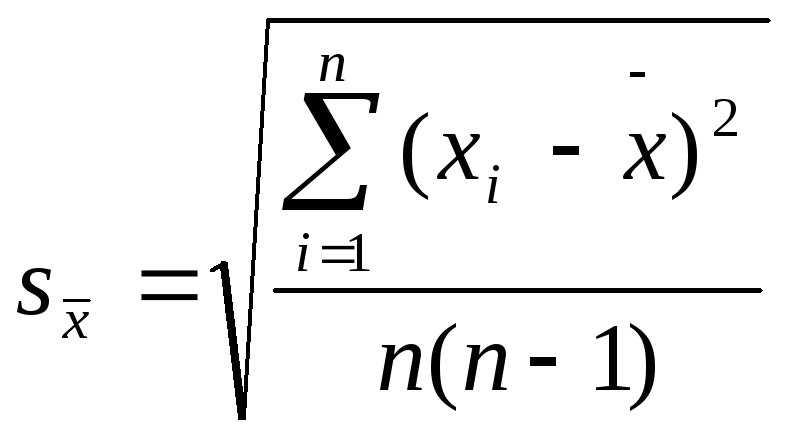
Следует отметить, что все величины – дисперсия, стандартное отклонение и относительное стандартное отклонение, а так же дисперсия среднего арифметического и стандартное отклонение среднего арифметического – характеризуют воспроизводимость результатов химического анализа.
Используемое при обработке небольших (n<20) выборок из нормально распределенной генеральной совокупности t – распределение (т.е. распределение нормированной случайной величины) характеризуется соотношением
![]()
где tp,f – распределение Стьюдента при числе степеней свободы f=n-1 и доверительной вероятности Р=0,95 (или уровня значимости р=0,05).
Значения t - распределения приведены в таблицах, по ним рассчитывают для выборки в n результатов величину доверительного интервала измеряемой величины для заданной доверительной вероятности по формуле
![]()
Доверительный интервал характеризует как воспроизводимость результатов химического анализа, так и – если известно истинное значение хист – их правильность.
Пример выполнения контрольной работы № 2
Задание
При анализе воздуха на содержание азота хроматографическим методом для двух серий опытов получены следующие результаты:
|
№ серии |
Результат определения азота в воздухе, % по объему | |||||||
|
1 |
77,95 |
78,08 |
77,90 |
77,92 |
78,10 |
78,05 |
78,07 |
77,99 |
|
2 |
78,08 |
78,13 |
78,02 |
78,16 |
78,20 |
78,26 |
78,14 |
78,23 |
Рассчитать среднее значение концентрации компонента и его доверительный интервал. Принадлежат ли результаты обеих выборок одной и той же генеральной совокупности.
Решение:
Проверяем ряды на наличие грубых ошибок по Q-критерию. Для чего их располагаем результаты в ряд по убыванию (от минимума к максимуму или наоборот) :
Первая серия:
77,90<77,92<77,95<77,99<78,05<78,07<78,08<78,10
Проверяем крайние результаты ряда (не содержат ли они грубую ошибку).
![]()
Полученное значение сравниваем с табличным (табл.2 приложения). Для n=8, p=0,95 Qтаб=0,55.
Т.к. Qтаб >Q1 расчет , левая крайняя цифра не является «промахом».
Проверяем крайнюю правую цифру
![]()
Qрасч<Qтаб, т.к. 0,1<0,55 (n=8, p=0,95).
Крайняя правая цифра так же не является ошибочной.
Располагаем результаты второго ряда в порядке их возрастания:
78,02<78,08<78,13<78,14<78,16<78,20<78,23<78,26.
Проверяем крайние результаты опытов - не являются ли они ошибочными.
![]()
Q (n=8, p=0,95)=0,55. Табличное значение.
![]() <Q(n=8,
p=0,95),
т.е. 0,25<0,55
<Q(n=8,
p=0,95),
т.е. 0,25<0,55
Крайнее левое значение – не ошибочное.
Крайняя правая цифра (не является ли она ошибочной).
![]()
![]() ,
т.е. 0,125<0,55
,
т.е. 0,125<0,55
Крайнее правое число не является «промахом».
Подвергаем результаты опытов статистической обработке.
Вычисляем средневзвешенные результатов:
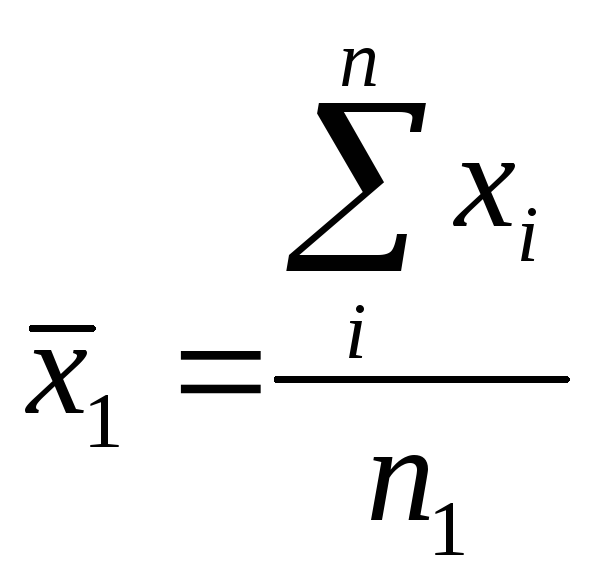 -
для первого ряда результатов.
-
для первого ряда результатов.
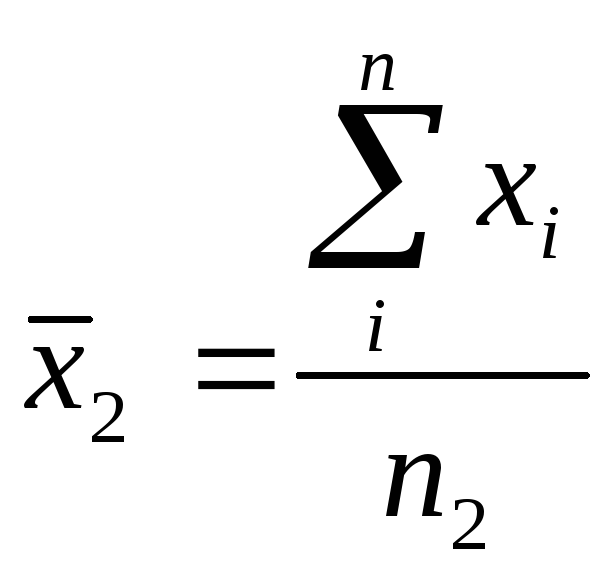 -
для второго ряда результатов.
-
для второго ряда результатов.
Дисперсия относительно среднего:
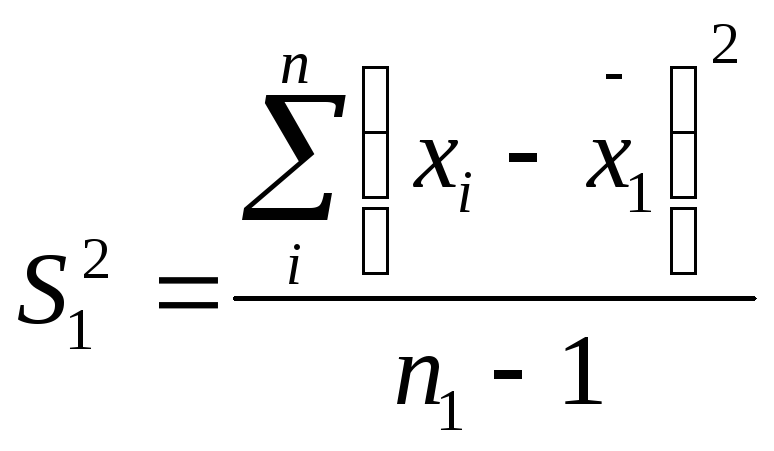 -
для первого ряда.
-
для первого ряда.
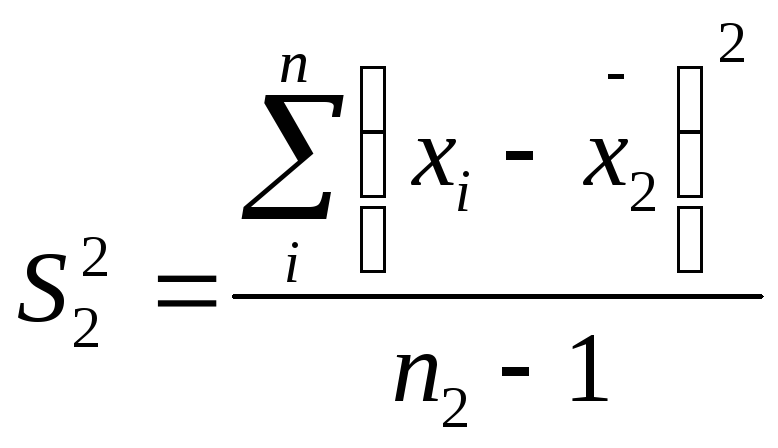 -
для второго ряда.
-
для второго ряда.
Стандартное отклонение:
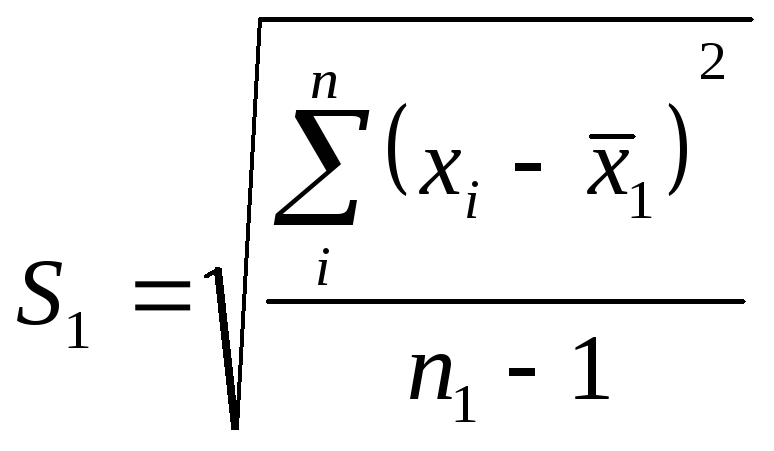 -
для первого ряда.
-
для первого ряда.
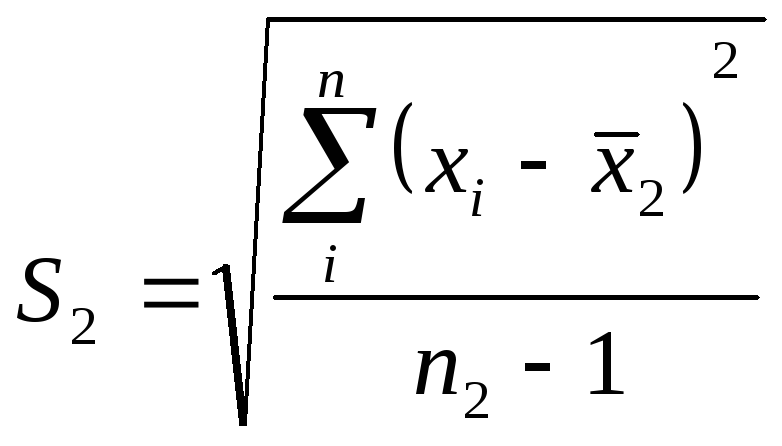 -
для второго ряда.
-
для второго ряда.
Стандартное отклонение среднего арифметического:
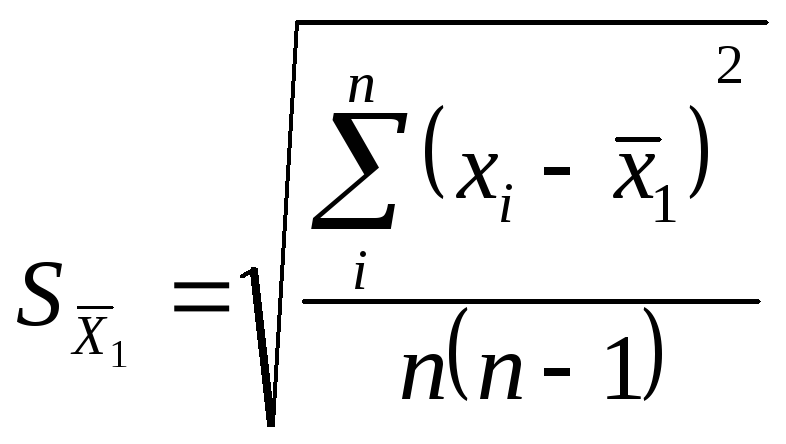
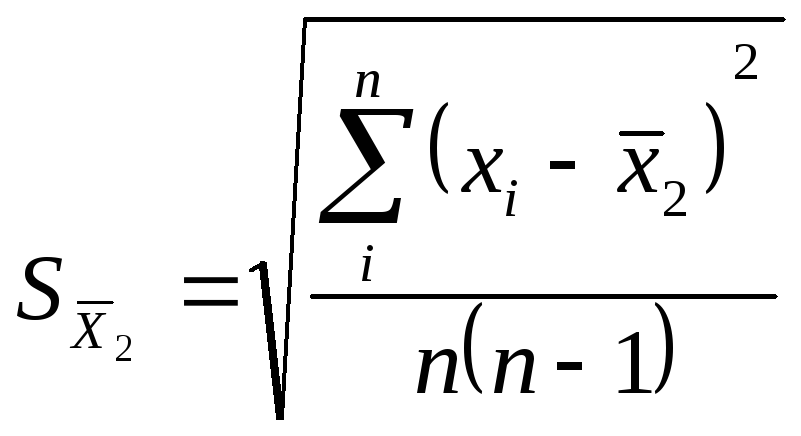
При небольших (n<20) выборках из нормально распределенной генеральной совокупности следует использовать t – распределение, т.е. распределение Стьюдента при числе степени свободы f=n-1 и доверительной вероятности p=0,95.
Пользуясь таблицами t – распределения, определяют для выборки в n – результатов величину доверительного интервала измеряемой величины для заданной доверительной вероятности. Этот интервал можно рассчитать:
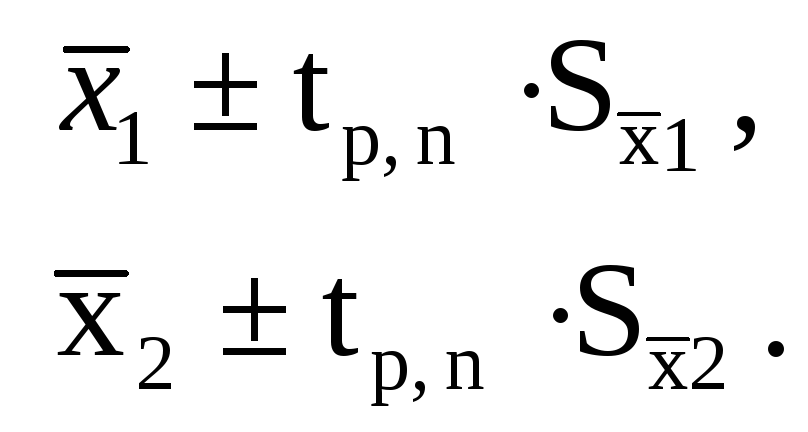
Сравниваем дисперсии и средние результаты двух выборочных совокупностей.
Сравнение двух дисперсий проводится при помощи F- распределения (распределения Фишера). Если мы имеем две выборочные совокупности с дисперсиями S21 и S22 и числами степеней свободы f1=n1-1 и f2=n2-1, соответственно, то рассчитываем значение F:
F=S21 / S22
Причем в числителе всегда находится большая из двух сравниваемых выборочных дисперсий. Полученный результат сравнивают с табличным значением. Если F0 > Fкрит (при р=0,95; n1, n2), то расхождение между дисперсиями значимо и рассматриваемые выборочные совокупности различаются по воспроизводимости.
Если расхождение между дисперсиями незначимо, возможно сравнить средние x1 и х2 двух выборочных совокупностей, т.е. выяснить, есть ли статистически значимая разница между результатами анализов. Для решения поставленной задачи используют t – распределение. Предварительно рассчитывают средневзвешенное двух дисперсий:
![]()
И
средневзвешенное стандартное отклонение
![]()
а затем – величину t:
![]()
Значение
tэксп
сравнивают с tкрит
при числе степеней свободы f=f1+f2=(n1+n2-2)
и выборочной доверительной вероятности
р=0,95. Если при этом tэксп
> tкрит
,то
расхождение между средними
![]() и
и
![]() значимо и выборка не принадлежит одной
и той же генеральной совокупности. Если
tэксп<
tкрит,
расхождение между средними незначимо,
т.е. выборки принадлежат одной и той же
генеральной совокупности, и, следовательно,
данные обеих серий можно объединить и
рассматривать их как одну выборочную
совокупность из n1+n2
результатов.
значимо и выборка не принадлежит одной
и той же генеральной совокупности. Если
tэксп<
tкрит,
расхождение между средними незначимо,
т.е. выборки принадлежат одной и той же
генеральной совокупности, и, следовательно,
данные обеих серий можно объединить и
рассматривать их как одну выборочную
совокупность из n1+n2
результатов.

Контрольное задание № 2
Анализ воздуха на содержание компонента Х хроматографическим методом для двух серий дал следующие результаты (таблица-1).
1. Для каждой из двух серий опытов рассчитать среднее значение концентрации компонента и его доверительный интервал (провести статистическую обработку результатов для двух серии опытов).
3. Принадлежат ли результаты обеих выборок и одной и той же генеральной совокупности. Проверить по критерию Стьюдента t (р = 0,95; n = 8).
Таблица-4.2.1- Исходные данные по контрольному заданию № 2
|
№ варианта |
Ком-понент |
№ серии |
Содержание компонента Х | |||||||
|
1 |
N2 |
I |
79,42 |
81,18 |
79,24 |
79,16 |
80,90 |
78,78 |
79,12 |
79,20 |
|
II |
79,75 |
80,81 |
79,94 |
79,90 |
80,74 |
80,74 |
79,68 |
79,91 | ||
|
2 |
O2 |
I |
18,80 |
18,90 |
18,95 |
18,82 |
18,76 |
18,93 |
18,91 |
18,97 |
|
II |
19,10 |
18,98 |
18,94 |
18,92 |
18,89 |
18,86 |
18,84 |
18,90 | ||
|
3 |
Ar2 |
I |
0,933 |
0,928 |
0,916 |
0,922 |
0,935 |
0,933 |
0,930 |
0,929 |
|
II |
0,945 |
0,942 |
0,939 |
0,937 |
0,940 |
0,944 |
0,938 |
0,936 | ||
|
4 |
N2 |
I |
78,08 |
78,20 |
78,34 |
78,28 |
78,50 |
78,32 |
78,47 |
78,11 |
|
II |
78,60 |
78,45 |
78,56 |
78,56 |
78,70 |
78,58 |
78,49 |
78,42 | ||
|
5 |
O2 |
I |
19,70 |
19,75 |
19,72 |
19,20 |
19,68 |
19,80 |
19,78 |
19,81 |
|
II |
20,68 |
20,56 |
20,54 |
20,60 |
20,52 |
20,55 |
20,42 |
20,40 | ||
|
6 |
Ar2 |
I |
0,956 |
0,954 |
0,952 |
0,956 |
0,953 |
0,958 |
0,957 |
0,956 |
|
II |
0,962 |
0,968 |
0,964 |
0,965 |
0,960 |
0,961 |
0,965 |
0,963 | ||
|
7 |
N2 |
I |
80,05 |
80,20 |
80,16 |
80,26 |
80,34 |
80,10 |
80,12 |
80,28 |
|
II |
79,98 |
80,06 |
79,90 |
80,26 |
80,15 |
80,30 |
80,29 |
80,31 | ||
|
8 |
O2 |
I |
20,95 |
20,88 |
20,93 |
21,00 |
20,89 |
20,98 |
20,92 |
20,90 |
|
II |
20,87 |
20,85 |
20,81 |
20,86 |
21,12 |
20,92 |
20,84 |
20,87 | ||
|
9 |
Ar2 |
I |
0,923 |
0,926 |
0,926 |
0,920 |
0,918 |
0,924 |
0,925 |
0,919 |
|
II |
0,932 |
0,936 |
0,928 |
0,929 |
0,930 |
0,935 |
0,940 |
0,938 | ||
|
10 |
N2
|
I |
77,95 |
78,08 |
77,90 |
77,92 |
78,10 |
78,05 |
78,07 |
77,99 |
|
II |
78,08 |
78,13 |
78,02 |
78,16 |
78,20 |
78,26 |
78,14 |
78,23 | ||
|
11 |
O2 |
I |
21,90 |
21,87 |
21,80 |
21,86 |
21,89 |
21,82 |
21,92 |
21,85 |
|
II |
21,78 |
21,85 |
21,92 |
21,89 |
21,84 |
21,89 |
21,95 |
21,98 | ||
|
12 |
Ar2 |
I |
0,954 |
0,956 |
0,953 |
0,549 |
0,548 |
0,950 |
0,952 |
0,949 |
|
II |
0,936 |
0,946 |
0,938 |
0,944 |
0,948 |
0,939 |
0,940 |
0,941 | ||
|
13 |
N2 |
I |
81,06 |
81,13 |
81,25 |
81,34 |
81,23 |
81,30 |
81,17 |
81,35 |
|
II |
81,25 |
81,03 |
81,32 |
81,29 |
81,19 |
81,10 |
81,28 |
81,15 | ||
|
14 |
O2 |
I |
20,34 |
20,66 |
20,38 |
20,45 |
20,48 |
20,41 |
20,40 |
20,36 |
|
II |
20,62 |
20,68 |
20,56 |
20,61 |
20,64 |
20,58 |
20,66 |
20,59 | ||
|
15 |
Ar2 |
I |
0,910 |
0,913 |
0,915 |
0,900 |
0,908 |
0,916 |
0,918 |
0,912 |
|
II |
0,920 |
0,926 |
0,921 |
0,928 |
0,923 |
0,926 |
0,927 |
0,922 | ||
|
16 |
N2 |
I |
78,65 |
78,56 |
78,63 |
78,50 |
78,70 |
78,60 |
78,69 |
78,63 |
|
II |
78,81 |
78,83 |
78,77 |
78,80 |
78,76 |
78,50 |
78,69 |
78,65 | ||
|
17 |
O2 |
I |
19,20 |
19,26 |
19,17 |
19,30 |
19,10 |
19,11 |
19,24 |
19,29 |
|
II |
18,98 |
18,88 |
19,00 |
19,10 |
19,05 |
19,03 |
19,01 |
19,09 | ||
|
18 |
Ar2 |
I |
0,956 |
0,959 |
0,962 |
0,964 |
0,965 |
0,963 |
0,952 |
0,960 |
|
II |
0,950 |
0,964 |
0,953 |
0,952 |
0,968 |
0,963 |
0,965 |
0,961 | ||
|
19 |
N2 |
I |
79,65 |
79,35 |
79,59 |
79,25 |
79,58 |
79,68 |
79,60 |
79,45 |
|
II |
79,42 |
79,00 |
79,39 |
79,48 |
79,60 |
79,36 |
79,40 |
79,37 | ||
|
20 |
O2 |
I |
21,30 |
21,35 |
21,46 |
21,33 |
21,42 |
21,36 |
21,40 |
21,43 |
|
II |
21,00 |
21,20 |
21,09 |
21,25 |
21,13 |
21,10 |
21,24 |
21,08 | ||
|
21
|
Ar2 |
I |
0,926 |
0928 |
0,930 |
0,929 |
0,932 |
0,935 |
0,927 |
0,934 |
|
II |
0,933 |
0,935 |
0,934 |
0,932 |
0,936 |
0,933 |
0,937 |
0,938 | ||
|
22 |
N2 |
I |
78,00 |
78,16 |
78,20 |
77,96 |
77,98 |
78,14 |
78,18 |
78,09 |
|
II |
78,31 |
78,26 |
78,15 |
77,80 |
78,36 |
78,29 |
78,29 |
78,21 | ||
|
23 |
O2 |
I |
20,60 |
20,69 |
20,59 |
20,61 |
20,63 |
20,69 |
20,61 |
20,68 |
|
II |
20,53 |
20,54 |
20,69 |
20,64 |
20,58 |
20,53 |
20,55 |
20,62 | ||
|
24 |
Ar2 |
I |
0,900 |
0,910 |
0,912 |
0,908 |
0,909 |
0,910 |
0,907 |
0,905 |
|
II |
0,910 |
0,916 |
0,920 |
0,926 |
0,924 |
0,927 |
0,930 |
0,925 | ||
|
25 |
N2 |
I |
81,19 |
81,34 |
81,00 |
81,29 |
81,26 |
81,17 |
81,21 |
81,21 |
|
II |
80,96 |
81,05 |
81,24 |
81,19 |
81,13 |
81,23 |
81,11 |
81,00 | ||
