Metodichka_ruchnoy_schet_chislennye_metody
.pdfЛАБОРАТОРНАЯ РАБОТА №1
Решение нелинейного уравнения с одной неизвестной. Методы отделения и уточнения корней
Постановка задачи. Для данного нелинейного уравнения y(x)=0 с одной неизвестной величиной на промежутке [a,b] отделить корни с шагом h (Шаговым методом) и уточнить корень с точностью ε:
методом половинного деления;
методом Ньютона;
методом простой итерации.
Идея метода
Название |
Выбор начального |
Итерационная |
Окончание |
метода |
значения |
формула |
процесса |
|
|
|
вычисления |
Шаговый |
x=a – левый конец |
y=f(x) – значение |
x1<=b |
метод |
промежутка [a,b] |
функции в точке x |
|
|
|
x1=x+h – следующее |
|
|
|
значение переменной |
|
|
|
y1=f(x1) - значение |
|
|
|
функция в точке x1 |
|
|
|
y*y1<0 - признак |
|
|
|
интервала изоляции |
|
Метод |
[a,b] – интервал |
x=(a+b)/2 – середина |
|f(x)|<ε |
половинного |
изоляции |
интервала |
|
деления |
|
f(a) –значение |
|
|
|
функции в точке a |
|
|
|
f(x) –значение |
|
|
|
функции в точке x |
|
|
|
если f(a)*f(x)<0, то |
|
|
|
выбираем [a,x] |
|
|
|
если f(a)*f(x)>0, то |
|
|
|
выбираем [x,b] |
|
Метод |
x0 = a или x0 = b |
f1(x) – первая |
|f(xi)|<ε |
Ньютона |
f2(x)-вторая |
производная функции |
|
|
производная функции f(x) |
f(x) |
|
|
f(x0)*f2(x0)>0 |
xi+1 = xi - f(xi)/f1(xi) |
|
Метод |
привести уравнение к |
xi+1= φ(xi) |
|f(xi)|<ε |
простой |
виду x= φ(x) |
|
|
итерации |
x0 = a или x0 = b |
|
|
(1-й способ) |
|φ(a)|<1 и |φ(b)|<1 |
|
|
Метод |
f1(x) – первая |
с=1/max(|f1(a)|;|f1(b)|) |
|f(xi)|<ε |
простой |
производная функции f(x) |
xi+1 = xi – c*f(xi) |
|
итерации |
если |f1(a)| > |f1(b)| ,то |
|
|
(2-й способ) |
x0=a |
|
|
|
если |f1(a)| < |f1(b)| ,то |
|
|
|
x0=b |
|
|
|
|
|
|
3
Постановка задачи:
1. Шаговым методом найти интервал изоляции корня нелинейного уравнения arccos( x) 
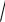1 0.3 x3 0 интервале [0; 1], шаг h = 0,1.
Ручной счет
arccos( x) 
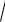1 0.3 x3 0
|
|
|
|
|
|
|
|
||
x0=0 |
F(x0)= arccos(0) |
1 0.5708 |
|||||||
|
|
|
|
|
|
|
|
|
|
x1=0+0.1=0.1 |
F(x1)= |
arccos(0.1) |
|
1 0.13 |
0.4708 |
||||
|
|
|
|
|
|
|
|
||
x2=0.1+0.1=0.2 |
F(x2)= |
arccos(0.2) |
|
1 0.23 0.3706 |
|||||
|
|
|
|
|
|
|
|
|
|
x3=0.2+0.1=0.3 |
F(x3)= |
arccos(0.3) |
|
1 0.33 |
|
0.2702 |
|||
|
|
|
|
|
|
|
|
|
|
x4=0.3+0.1=0.4 |
F(x4)= |
arccos(0.4) |
|
|
1 0.43 |
0.1689 |
|||
|
|
|
|
|
|
|
|
||
x5=0.4+0.1=0.5 |
F(x5)= |
arccos(0.5) |
|
1 0.53 |
0.0661 |
||||
|
|
|
|
|
|
|
|
||
x6=0.5+0.1=0.6 |
F(x6)= |
arccos(0.6) |
|
|
1 0.63 |
0.3998 |
|||
Вывод: в точке х=0.5 F(x5)>0, в точке х=0.6 F(x6)<0, то есть функция меняет знак на отрезке [0.5; 0.6]. Следовательно, найден интервал, содержащий корень.
2. Методом Ньютона найти корень с точностью ε=0,01 на интервале
[0.5;0.6]
Ручной счет |
|
Проверка условия сходимости |
f (x0 ) f "(x0 ) 0 , где |
x0 – начальное приближение,
f(x0) – значение функции в точке x0,
f”(x0) – значение второй производной функции в точке x0.
f '(x) |
|
|
0,9 x2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 0,3 |
x3 |
|
1 x2 – первая производная функции f(x) |
|||||||||||||||||||
2 |
|
|
|||||||||||||||||||||
f ''(x) |
|
|
|
0,9 x |
|
|
|
|
|
|
|
0,81 x |
4 |
|
|
|
|
x |
|
– вторая производная функции f(x) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
1 |
0,3 x3 |
4 |
|
|
(1 0,3 |
x3 )3 |
(1 x2 )3 |
|
|
|||||||||||
Проверяем условие сходимости в крайних точках интервала [0.5; 0.6]:
x0=0,5 |
f(x0)=0,0661 f”(x0) |
f (x0 ) f "(x0 ) 0 |
условие сходимости не выполняется, |
||
x0=0,6 |
f(x0)= –0,3998 |
f”(x0)= –0,584 |
f (x0 ) f "(x0 ) 0 условие сходимости |
||
выполняется. |
|
|
|
|
|
За начальное приближение выбираем x0=0,6. |
|
||||
Итерационная формула метода xi 1 xi |
|
f (xi ) |
. |
||
|
f '(xi ) |
||||
|
|
|
|
|
|
4
Вычислим первое приближение к корню:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(x0)= arccos(0,6) 1 0.3 0,63 |
0,3998 |
|||||||||||||||||||||
|
f '(x0 ) |
|
|
0,9 0,62 |
|
|
1 |
|
|
|
1,0824 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 0,3 0,63 |
1 0,62 |
|||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|||||||||||||||
|
x1 x0 |
|
f (x0 ) |
|
0,6 |
|
( 0,3998) |
|
0,5633 |
|||||||||||||
|
|
f '(x0 ) |
|
( 1,0824) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Находим значение функции f(x) в полученной точке |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
f(x1)= arccos(0,5633) |
|
|
1 0.3 0,56333 3,66 10 4 . |
|||||||||||||||||||
|
f (x1 ) |
|
0,000366 0,01 , |
следовательно, корень найден на первой итерации |
||||||||||||||||||
|
|
|||||||||||||||||||||
х=0,5633. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Документ Mcad |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3. Методом половинного деления найти корень с точностью ε=0,01 на интервале [0.5; 0.6]
Ручной счет
Делим интервал изоляции корня пополам, т.е. находим среднюю точку хс
xc |
a b |
|
0,5 |
0,6 |
0,55. |
|
|
|
|||
2 |
|
2 |
|
|
|
Вычислим значение функции в левом конце f(0,5)= arccos(0,5) 
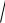1 0.3 0,53 0,066 .
5
Вычислим значение функции в средней точке хс f(0,55)= arccos(0,55) 
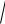1 0.3 0,553 0,014 ,
находим их произведение
f (0,6) f (0,55) 0,066 0,014 9,24 10 4 0 .
Произведение положительное, следовательно, на левом отрезке корня нет, корень находится на правом отрезке [0.55; 0.6].
Модуль значения функции точке хс=0,55 больше заданной точности, т.е. f (0,55) 0,014 0,01, поэтому делаем следующий шаг.
На интервале [0.55; 0.6] находим среднюю точку хс
xc |
a b |
|
0,55 0,6 |
0,575 . |
|
|
|||
2 |
|
2 |
|
|
Вычислим значение функции в левом конце f(0,55)= arccos(0,55) 
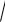1 0.3 0,553 0,014 .
Вычислим значение функции в средней точке хс f(0,575)= arccos(0,575) 
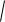1 0.3 0,5753 0,0129 ,
находим их произведение
f (0,55) f (0,575) 0,014 ( 0,0129) 1,806 10 4 0 .
Произведение отрицательное, следовательно, корень находится на левом отрезке [0.55;0.575].
Модуль значения функции точке хс=0,575 больше заданной точности, т.е. f (0,55) 0,0129 0,01, поэтому делаем следующий шаг.
На интервале [0.55;0.575] находим среднюю точку хс
xc |
a b |
|
0,55 0,575 |
0,5625 . |
|
|
|||
2 |
|
2 |
|
|
Вычислим значение функции в левом конце f(0,55)= arccos(0,55) 
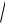1 0.3 0,553 0,014 .
Вычислим значение функции в средней точке хс
f(0,5625)= arccos(0,5625) |
1 0.3 0,56253 |
|
0,00045, |
находим их произведение |
|
|
|
f (0,55) f (0,5625) 0,014 0,00045 6,3 10 6 |
0 . |
||
Произведение положительное, следовательно, корень находится на правом отрезке [0.5625;0.575].
Модуль значения функции точке хс=0,5625 меньше заданной точности, т.е.
f (0,5625) 0,00045 0,01, поэтому итерационный процесс закончен, корень найден на третьем шаге х=0,5625.
6
Документ Mcad
4. Методом простой итерации найти корень с точностью ε=0,001 на интервале [0.5; 0.6]
Ручной счет |
|
|
|
|
|
|
|
|
|
|
|
Заменим исходное уравнение arccos( x) |
1 0.3 x3 |
0 |
(1) |
||
|
|
|
|
|
|
эквивалентным x cos( |
1 0.3 x3 ) |
|
|
(2) |
|
Обозначим правую часть уравнения (2) как функцию (x) cos(
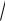1 0.3 x3 ) . Проверим условия сходимости в крайних точках интервала [0.5; 0.6].
Должны выполняться условия: |
|
'(0,5) |
|
|
|
1 и |
|
'(0,6) |
|
|
1. |
|
|
|||||||
|
|
|
|
|
|
|||||||||||||||
Находим первую производную функции (x) |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
'(x) |
0.45 x2 |
sin 1 0.3 x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
. Вычислим модули значений первой производной |
|||||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
1 0.3 x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
функции (x) |
точках х=0,5 и х=0,6: |
|
|
'(0,5) |
|
0,095 1, |
|
|
'(0,6) |
|
0,138 1. |
|||||||||
|
|
|
|
|
|
|||||||||||||||
Условие сходимости выполняется, поэтому за начальное приближение можно взять любой конец интервала. Пусть начальное приближение х0 = 0,5.
Итерационная формула метода: xi 1 |
(xi ) |
|
(3) |
||
|
|
|
|
|
|
Находим первое приближение к корню: х |
=0,5 |
x cos( |
1 0.3 0,53 ) 0,5561. |
||
|
0 |
|
1 |
|
|
7
|
|
|
В полученной точке находим значение функции f (x) arccos( x) |
1 0.3 x3 , |
|
которая является левой частью уравнения (1) |
|
|
f (0,5561) arccos(0,5561) 
1 0.3 0,55613 0,0072 .
Модуль значения функции точке х1=0,5561 больше заданной точности, т.е. f (0,5561) 0,0072 0,001, поэтому делаем следующий шаг.
За начальное приближение берем точку х1 = 0,5561. Находим второе приближение к корню:
х1=0,5561 x2 cos(
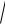1 0.3 0,55613 ) 0,5621.
В полученной точке находим значение функции f(x): f (0,5621) arccos(0,5621) 
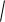1 0.3 0,56213 0,0008 .
Модуль значения функции точке хс=0,5561 меньше заданной точности, т.е. f (5621) 0,0008 0,001, поэтому итерационный процесс закончен, корень
найден на втором шаге х=0,5621.
Документ Mcad
8
ЛАБОРАТОРНАЯ РАБОТА №2
Решение систем линейных уравнений. Прямые и итерационные методы
Название |
|
|
Начальное |
|
|
|
Итерационная формула |
|
|
|
|
|
|
Остановка |
||||||||||||||
метода |
|
|
приближение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
процесса |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вычисления |
||
Метод |
|
Определитель |
|
|
Прямой ход – приведение |
|
|
|
|
|
|
|
Получение |
|||||||||||||||
Гаусса |
|
матрицы не равен |
|
матрицы к треугольному виду |
|
|
|
|
значений |
|||||||||||||||||||
|
|
нулю |
|
|
|
|
|
Обратный ход – вычисление |
|
|
|
|
|
|
всех |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
неизвестных, начиная с |
|
|
|
|
|
|
|
неизвестных |
|||||||||||
|
|
|
|
|
|
|
|
|
последнего уравнения |
|
|
|
|
|
|
|
|
|
|
|
||||||||
Метод |
|
Проверка условия |
|
x i 1 |
|
|
B ( A x2i A x3i A x4i |
) |
|
|
|
|x1i+1-x1i|<ε |
||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
12 |
|
13 |
|
14 |
|
|
|
|
|
|
i+1 |
i |
|
|||||
простой |
|
сходимости |
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|<ε |
||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|x2 |
-x2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
итерации |
|
|A11|>|A12|+|A13|+|A14| |
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|x3i+1-x3i|<ε |
|||||||
|
|
x2i 1 |
|
|
B ( A x i |
A x i |
A x i ) |
|
|
|
|
|||||||||||||||||
|
|
|A22|>|A21|+|A23|+|A24| |
|
|
|
|
2 |
21 |
1 |
23 3 |
|
24 4 |
|
|
|
|
|
|
|x4i+1-x4i|<ε |
|||||||||
|
|
|
|
|
|
|
|
A22 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|A33|>|A31|+|A32|+|A34| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
B ( A x i |
A x i A x i ) |
|
|
|
|
|
|
|
|||||||||||||
|
|
|A44|>|A41|+|A42|+|A43| |
|
x3i 1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
3 |
31 |
1 |
32 2 |
|
34 4 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
A33 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Выбор начального |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
приближения |
|
|
|
|
|
|
|
|
|
|
i |
i |
|
i |
|
|
|
|
|
|
|
|
|
|||
|
|
0 |
|
0 |
|
0 |
|
|
x i 1 |
B4 ( A41x1 |
A42x2 |
A43x3 ) |
|
|
|
|
|
|
|
|
|
|||||||
|
|
=0 x2 |
=0 x3 |
=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
x1 |
|
|
|
4 |
|
|
|
|
|
|
A44 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x40=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Метод |
|
Проверка условия |
|
x i 1 |
|
|
B ( A x2i A x3i A x4i |
) |
|
|
|
|x1i+1-x1i|<ε |
||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
12 |
|
13 |
|
14 |
|
|
|
|
|
|
i+1 |
i |
|
|||||
Зейделя |
|
сходимости |
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|<ε |
||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|x2 |
-x2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|A11|>|A12|+|A13|+|A14| |
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|x3i+1-x3i|<ε |
|||||||
|
|
|
x2 i 1 |
|
|
B ( A |
x i 1 A |
x i |
A |
x i ) |
|
|
||||||||||||||||
|
|
|A22|>|A21|+|A23|+|A24| |
|
|
|
|
2 |
21 |
1 |
23 |
3 |
24 |
4 |
|
|
|
|x4i+1-x4i|<ε |
|||||||||||
|
|
|
|
|
|
|
|
A22 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|A33|>|A31|+|A32|+|A34| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
B3 ( A31x1i 1 A32 x2 i 1 A34 x4 i |
|
|
|
|
|
||||||||||||||||
|
|
|A44|>|A41|+|A42|+|A43| |
|
|
i 1 |
|
|
) |
|
|
|
|
||||||||||||||||
|
|
Выбор начального |
|
x3 |
|
|
|
|
|
A33 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
приближения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x 0=0 x |
0=0 x 0=0 |
|
|
|
|
|
B |
4 |
( A x i 1 A x i 1 |
A x i 1 ) |
|
|
|
|||||||||||||
|
|
10 |
2 |
|
3 |
|
|
|
x4 i 1 |
|
|
|
41 1 |
42 2 |
43 3 |
|
|
|
|
|
|
|
||||||
|
|
=0 |
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
44 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Постановка задачи: решить систему линейных уравнений |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
7 x1 2 x2 x3 x4 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3 x1 9 x2 |
|
x3 2 x4 7 |
|
(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x1 2 x2 |
11 x3 x4 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3 x2 2 x3 13 x4 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ручной счет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 Метод Гаусса |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Идея метода: последовательно исключаем переменные x1, x2, x3, пока в |
|
|
||||||||||||||||||||||||||
последней строке не будет однозначно определена переменная x4. |
|
|
|
|
|
|||||||||||||||||||||||
Запишем систему в виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
7 |
2 |
|
-1 |
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3 |
-9 |
|
1 |
|
|
2 |
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
-2 |
|
11 |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
3 |
|
-2 |
|
|
13 |
|
|
-3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
9
Разделим 1-ю строку на (7). Разделим 2-ю строку на (3):
1 |
0,286 |
-0,143 |
0,143 |
0,286 |
1 |
-3 |
0,333 |
0,667 |
2,333 |
1 |
-2 |
11 |
1 |
1 |
0 |
3 |
-2 |
13 |
-3 |
Исключаем из 2-й и 3-й строк переменную х1, для этого вычитаем 2-ю строку из 1-й и вычитаем 3-ю строку из 1-й:
1 |
0,286 |
-0,143 |
0,143 |
0,286 |
0 |
3,286 |
-0,476 |
-0,524 |
-2,048 |
0 |
2,286 |
-11,143 |
-0,857 |
-0,714 |
0 |
3 |
-2 |
13 |
-3 |
Разделим 2-ю строку на (3,286). Разделим 3-ю строку на (2,286). Разделим 4-ю строку на (3):
1 |
0,286 |
-0,143 |
0,143 |
0,286 |
0 |
1 |
-0,145 |
-0,159 |
-0,623 |
0 |
1 |
-4,875 |
-0,375 |
-0,313 |
0 |
1 |
-0,667 |
4,333 |
-1 |
Исключаем из 3-й и 4-й строк переменную х2, для этого вычитаем 3-ю строку из 2-й и вычитаем 4-ю строку из 2-й:
1 |
0,286 |
-0,143 |
0,143 |
0,286 |
0 |
1 |
-0,145 |
-0,159 |
-0,623 |
0 |
0 |
4,730 |
0,216 |
-0,311 |
0 |
0 |
0,522 |
-4,493 |
0,377 |
Разделим 3-ю строку на (4,73). Разделим 4-ю строку на (0,522):
1 |
0,286 |
-0,143 |
0,143 |
0,286 |
0 |
1 |
-0,145 |
-0,159 |
-0,623 |
0 |
0 |
1 |
0,046 |
-0,066 |
0 |
0 |
1 |
-8,611 |
0,722 |
Исключаем из 4-й строки переменную х3, для этого вычитаем 4-ю строку из 3-й:
1 |
0,286 |
-0,143 |
0,143 |
0,286 |
0 |
1 |
-0,145 |
-0,159 |
-0,623 |
0 |
0 |
1 |
0,046 |
-0,066 |
0 |
0 |
0 |
8,657 |
-0,788 |
Разделим 4-ю строку на (8,657): |
|
|||
1 |
0,286 |
-0,143 |
0,143 |
0,286 |
0 |
1 |
-0,145 |
-0,159 |
-0,623 |
0 |
0 |
1 |
0,046 |
-0,066 |
0 |
0 |
0 |
1 |
-0,091 |
Из 4-й строки выражаем x4: |
x4= -0,091 |
|||
Из 3-й строки выражаем x3: х3+0,046 х4= -0,066, откуда находим х3= -0,0615 Из 2-й строки выражаем x2:
х2-0,145 х3-0,159 х4= -0,623, откуда находим х2= -0,646
Из 1-й строки выражаем x1:
х1+0,286 х2-0,143 х3+0,143 х4= 0,286, откуда находим х1= 0,474.
Решение:
х1= 0,474, х2= -0,646, х3= -0,0615, x4= -0,091.
10
Метод простой итерации Постановка задачи: методом простой итерации найти корни системы
линейных уравнений (1) с точностью =0,1 Проверка условия сходимости.
Для сходимости метода необходимо и достаточно, чтобы в матрице А абсолютные значения всех диагональных элементов были больше суммы
|
aii |
|
|
|
|
|
aij |
|
модулей всех остальных элементов в соответствующей строке, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
i 1,i j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
7 |
|
|
|
2 |
|
|
|
1 |
|
|
|
1, |
|
9 |
|
|
|
3 |
|
|
|
1 |
|
|
|
2 |
|
, |
|
11 |
|
|
|
1 |
|
|
|
2 |
|
|
|
1, |
|
13 |
|
|
|
0 |
|
|
|
3 |
|
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Условие сходимости выполнено. Если условие сходимости выполнено, то на следующем этапе необходимо задать начальное приближение вектора неизвестных, в качестве которого обычно выбирается нулевой вектор:
x(0) |
x(0) |
x(0) |
x(0) |
0 |
(2) |
|
1 |
2 |
3 |
|
4 |
|
|
Заметим, |
что |
здесь |
и |
в дальнейшем нижний |
индекс обозначает |
|
соответствующую компоненту вектора неизвестных, а верхний индекс – номер итерации (приближения).
В результате каждой итерации получается новое значение вектора неизвестных. Для организации итерационного процесса запишем систему (1) в приведенном виде. Приведенная система уравнений имеет вид:
x(k 1) |
|
[b (a |
|
x(k ) ... |
a |
|
x(k ) )] |
|
|
||||
1 |
12 |
2 |
1n |
|
n |
|
|
||||||
1 |
|
|
|
|
a11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(k 1) |
|
[b (a |
21 |
x(k ) ... |
a |
2n |
x(k ) )] |
|
|
||||
2 |
|
1 |
|
|
n |
|
|
||||||
2 |
|
|
|
|
a22 |
|
|
|
|
|
|
(3) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
................................................................ |
|||||||||||||
x(k 1) |
|
[b (a |
n1 |
x(k ) ... |
a |
n,n 1 |
x(k ) |
)] |
|||||
n |
|
1 |
|
n 1 |
|
|
|||||||
n |
|
|
|
|
ann |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итерационный процесс заканчивается, если для каждой i-й компоненты вектора
|
|
|
|
|
|
|
|
|
< |
|||||||||||
неизвестных будет выполнено условие достижения точности: |
xi(k ) xi(k 1) |
|||||||||||||||||||
Для системы (1) приведенная система имеет вид: |
|
|
|
|
|
|
|
|
|
|||||||||||
x1 |
|
2 2x2 x3 |
x4 ) |
|
|
x(1) |
|
2 |
0,2857 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
7 |
|
|
|
|
|
|
1 |
|
7 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x2 |
|
|
7 3x1 |
x3 2x4 |
x(1) |
|
|
7 |
0,7778 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
9 |
|
|
|
|
2 |
|
9 |
|
|
|
(4) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x3 |
|
1 x1 2x2 |
x4 |
|
|
(1) |
|
1 |
|
0,0909 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
11 |
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
11 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
3 3x2 |
2x3 |
|
|
|
|
|
|
|
|
|
|||||||
x4 |
|
|
|
|
(1) |
|
|
3 |
0,2308 |
|
|
|||||||||
13 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
x4 |
13 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Проверка на точность: |
|
x(1) x(0) |
|
0,2857 0,1 , делаем следующий шаг. |
|
|
||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11
Вторая итерация: подставляем значения корней, полученные на первой итерации в систему (4)
x |
(2) |
|
2 2( 0,7778) 0,0909 ( 0,2308) |
0,5539 |
|
||
|
|
|
|
||||
1 |
7 |
|
|
|
|
||
|
|
|
|
|
|
||
x |
(2) |
7 3 0,2857 0,0909 2( 0,23080) 0,7237 |
|
||||
|
2 |
9 |
|
|
|
|
|
|
|
|
|
|
|
||
x |
(2) |
|
1 0,2857 2( 0,7778) ( 0,2308) |
|
0,0555 |
|
|
3 |
|
|
|||||
|
11 |
|
|
|
|
||
|
|
|
|
|
|
||
x4(2) |
3 3( 0,7778) 2 0,0909 |
0,0373 |
. |
||||
|
|
13 |
|
|
|
|
|
Проверка на точность: |
|
|
|
|
|||
x1(2) x1(i1) 0,5539 0,2857 0,2682 0,1, делаем следующий шаг.
Третья итерация: подставляем значения корней, полученные на второй итерации в систему (4)
x(3) |
|
2 2( 0,7237) ( 0,0555) ( 0,0373) |
0,4899 |
|||||||||
|
|
|||||||||||
1 |
7 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
x(3) |
7 3 0,5539 ( 0,0555) 2( 0,0373) 0,6076 |
|||||||||||
2 |
9 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
x(3) |
|
1 0,5539 2( 0,7237) ( 0,0373) |
0,0876 |
|||||||||
|
||||||||||||
3 |
11 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
x(3) |
3 3( 0,7237) 2( 0,0555) 0,0723 |
|||||||||||
4 |
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x(2) |
|
|
|
0,4899 0,5539 |
|
0,064 0,1 , |
||||
Проверка на точность: |
x(3) |
|
|
|
||||||||
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2(3) x2(2) 0,6033 ( 0,5539) 0,116 0,1, делаем следующий шаг.
Четвертая итерация: подставляем значения корней, полученные на третьей итерации в систему (4):
x(4) |
|
2 2( 0,6076) ( 0,0876) ( 0,0723) |
0,4571 |
|
|
|
|||
1 |
7 |
|
|
|
|
|
|
||
x(4) |
7 3 0,4899 ( 0,0876) 2( 0,0723) 0,6403 |
|||
2 |
9 |
|
|
|
|
|
|
||
x(4) |
|
1 0,4899 2( 0,6076) ( 0,0723) |
0,0575 |
|
|
||||
3 |
11 |
|
|
|
|
|
|
||
x(4) |
3 3( 0,6076) 2( 0,0723) 0,104 |
|||
4 |
13 |
|
|
|
|
|
|
||
Проверка на точность: x1(4) x1(3) 0,4571 0,4899 0,0328 0,1,
x(4) |
x(3) |
|
|
0,6403 ( 0,6076) |
|
0,033 0,1, |
|
|
|||||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
x3(4) x3(3) 0,0575 ( 0,0876) 0,03 0,1
12