- •1.1 Случайные события: элементарные, достоверные, невозможные, несовместные, совместные, равновозможные. Попарно-несовместные, образующие полную группу. Пространство элементарных событий. Случай.
- •1.2. Сумма, произведение, разность, отрицание. Теоретико-множественная трактовка. Диаграммы Эйлера-Венна. Алгебра событий. Понятие сигма-алгебры.
- •1.3. Частота события. Свойство статистической устойчивости. Статистическое определение вероятности.
- •1.4. Классическое определение вероятности события. Непосредственное вычисление вероятностей.
- •1.5. Комбинаторика: правило умножения и сложения. Основные схемы: с возвращением, без возвращения. Понятия размещения, сочетания, перестановки.
- •1.6. Геометрическое определение вероятности.
- •1.7. Аксиоматическое определение вероятности. Свойства вероятностей.
- •1.8. Вероятностное пространство.
- •Независимые случайные величины Определения
- •1.12 Вероятность суммы событий
- •1.13 Формула полной вероятности.
- •1.14 Формула Байеса
- •1.15.Однородная цепь Маркова
- •1.16. Независимые испытания. Схема и формула Бернулли. Многоугольник распределения вероятностей.
- •1.17 . Предельные теоремы в схеме Бернулли: формула Пуассона, локальная и интегральная теоремы Муавры-Лапласа.
- •1.18 Схема Бернулли. Наивероятнейшее число
- •2.1.Понятие и определение случайной величины.
- •2.2. Закон распределения случайной величины. Многоугольник распределения.
- •2.3. Дискретные и непрерывные случайные величины
- •2.4.Дискретные случайные величины. Сумма, разность, произведение на число.
- •2.5. Произведение д.С.В. Независимость.
- •2.9. Числовые характеристики случайных величин. Мат ожидание. Свойства мат ожидания.
- •2.10. Числовые характеристики случайных величин. Дисперсия. Свойства. Среднее квадратное отклонение
- •2.11. Числовые характеристики случайных величин. Квантили. Мода, медиана. Начальные и центральные моменты.
- •2.12. Производящая функция (случай целочисленных случайных величин).
- •3.1. Понятие системы случайных величин. Закон распределения в дискретном случае.
- •3.8 Числовые характеристики. Математическое ожидание и дисперсия. Центр рассеивания.
- •3.9 Корреляционный момент. Свойства ковариации. Ковариационная матрица.
- •3.10 Коэффициент корреляции. Свойства. Линейная корреляционная зависимость.
- •3.11 Двумерное нормальное распределение. Центр рассеивания. Формула вероятности
- •3.12 Условное мат. Ожидание. Регрессия. Коэффициент линейной регрессии.
- •5.1 Неравенство Чебышёва
- •5.2 Неравенство Маркова для с.В. Принимающих неотрицательные значения
- •5.3 Сходимость по вероятности
- •5.4 Закон больших числе в форме Чебышёва
- •5.5 Закон больших чисел в форме Бернулли (схема Бернулли)
- •5.6 Центральная предельная теорема (формулировка, пример применения для решения задач)
- •5.7 Центральная предельная теорема в случае схемы Бернулли (теорема Муавра-Лапласа).
- •Глава 1. Случайные события
- •Глава 2. Случайные величины
- •Глава 3. Системы случайных величин
- •Глава 5. Предельные теоремы
2.10. Числовые характеристики случайных величин. Дисперсия. Свойства. Среднее квадратное отклонение
Дисперсия дискретной случайной величины есть математическое ожидание квадрата отклонения случайной величины от её математического ожидания: D(X) = (x1 - M(X))2p1 + (x2 - M(X))2p2 + ... + (xn- M(X))2pn = x21p1 + x22p2 + ... + x2npn - [M(X)]2
Свойства дисперсии. 1) Дисперсия постоянной величины равна нулю: D(С) = 0 2) Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(СХ) = С2 · D(Х) 3) Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых: D(Х1 ± Х2 ± ... ± Хn) = D(Х1) + D(Х2) + ... + D(Хn)
Среднее квадратическое отклонение дискретной случайной величины, оно же стандартное отклонение или среднее квадратичное отклонение есть корень квадратный из дисперсии: σ(X) = √D(X)
2.11. Числовые характеристики случайных величин. Квантили. Мода, медиана. Начальные и центральные моменты.
Мода дискретной случайной величины Mo(X) - это значение случайной величины, имеющее наибольшую вероятность. На многоугольнике распределения мода - это абсцисса самой высокой точки. Бывает, что распределение имеет не одну моду.
Начальным моментом порядка k случайной величины Х называется матема-тическое ожидание величиныXk:
νk = M (Xk).
В частности, ν1 = М(Х), ν2 = М(Х2). Следовательно, дисперсия D(X) = ν2 — ν1².
Центральным моментом порядка k случайной величины Х называется мате-матическое ожидание величины (Х — М(Х))k:
μk = M((Х — М(Х))k)
Медианой Ме непрерывной случайной величины называют такое ее значение, для которого
p( X < Me ) = p( X > Me ).
Графически прямая х = Ме делит площадь фигуры, ограниченной кривой распределения, на две равные части.
Для случайной величины Х с функцией распределения F(X) квантилью порядка р (0 < p < 1) называется число Кр такое, что F(Kp) ≤ p, F(Kp + 0) ≥ p. В частности, если F(X) строго монотонна, Кр: F(Kp) = p.
2.12. Производящая функция (случай целочисленных случайных величин).
Это частный случай Хар.функции.
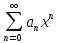
Свойства.
Если
Х=m(целые
числа), то
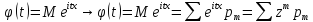
Z=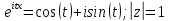
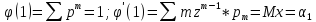
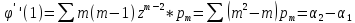
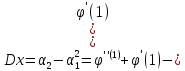
2.13.Биноминальный закон распределения.
Это распределение вероятностей возможных чисел появления события А при n независимых испытаниях, в каждом из которых событие А может осуществиться с одной и той же вероятностью Р(А)=р=const. Кроме события А может произойти также противоположное событие, вероятность которого Р(А)=1-p=q.
Вероятности любого числа событий соответствуют членам разложения бинома Ньютона:
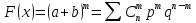
Числовые характеристики Бин. распределения:
М(m)=np
; D(m)=npq;
Ϭ(m)=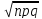
2.14.Закон распределения Пуассона.
Это распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой частотой и независимо друг от друга.
Р(м)=р(Х=м)=(ам/м!)*е-а
Условие
нормировки: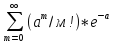 =1
=1
2.15.Геометрический закон распределения
Это распределение дискретной случайной величины равной количеству испытаний до первого успеха.
Р(Х=м)=qм-1р; Mx=q/p; Dx=q/p2
Условие
нормировки: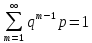
Ф.
распределения:
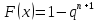
2.16. Гипергеометрический закон распределения.
Это распределение количества удачных выборок без возвращения из конечной совокупности (см. задачу про выборку карт).
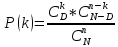
2.17. Равномерно распределение
Непрерывная величина Х имеет равномерное распределение на отрезке от а до в, если на этом отрезке плотность распределения вероятности случайной величины постоянна, т.е. если диф.фукция распределения f(x) имеет следующий вид:
 ;
Mx=(a+b)/2; Dx=(b-a)2/12
;
Mx=(a+b)/2; Dx=(b-a)2/12
Св-ва распределения:
F(x)
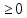 ;
;P{X
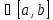 }=F(b)-F(a)=
}=F(b)-F(a)=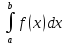

2.18. Экспоненциальный закон распределения
Это абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.
Ф.распределения:
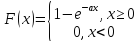 ;
Mx=a-1;
Dx=a-2
;
Mx=a-1;
Dx=a-2
2.19. Нормальный закон распределения
(Гауссово распределение) распределение, которое в одномерном случае задаётся функцией плотности вероятности, совпадающей с функцией Гаусса:
F(x)=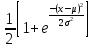 ;
Mx=
;
Mx=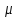 ; Dx=
; Dx=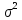
2.20. Характеристическая функция. Свойства. Характеристическая функция нормального
Распределения
Это один из способов задания распределения. Характеристические функции могут быть удобнее в тех случаях, когда, например, плотность или функция распределения имеют очень сложный вид.
Св-ва:
Характеристическая функция однозначно задаёт распределение(к примеру, если обе С.В. абсолютно непрерывны, то совпадение характ.функций лечёт совпадение плотностей)
Х.ф. всегда ограниченна:
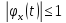
Х.ф. в нуле равна 1:
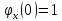
Х.ф. всегда непрерывна:
Х.ф. однородна как ф. случайной величины:
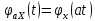
Х.ф. суммы независимых С.величин равна произведению х.функций
Для всех вещественных t верно равенство
 ,где
,где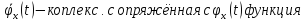
Теор.Леви.Пусть F-функция распределения,а
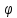 -её
Х.ф.Если а и в-точки непрерывностиF.
-её
Х.ф.Если а и в-точки непрерывностиF.
Х.ф.
нормального распределения: