
- •Колебания и волны
- •Обратная величина
- •Задание
- •Контрольные вопросы
- •Список литературы
- •Лабораторная работа № 23 свободные электромагнитные колебания
- •Характеристика электромагнитных колебаний
- •Период затухающих колебаний т определится по формуле
- •Приведем другие выражения для измерения добротности ,
- •Описание установки и метода измерений
- •Задание
- •Контрольные вопросы
- •Список литературы
- •Пусть эдс источника изменяется по гармоническому закону
- •Будем искать частное решение уравнения
- •Приведем другие выражения для добротности ,
- •Из формул (25.13) и (25.14) следует, что
- •Методика измерений
- •Задание
- •Колебательного контура и пунктов задания
- •Контрольные вопросы
- •Список литературы
- •Бегущие волны описываются волновым уравнением
- •Описание установки
- •Задание
- •Контрольные вопросы
- •Список литературы
- •Метод измерения
- •Задание к работе
- •Контрольные вопросы
- •Список литературы
- •Осциллографа оцл2-02 Краткое описание
- •Порядок работы
- •Литература
Пусть эдс источника изменяется по гармоническому закону
![]() .
(25.1)
.
(25.1)
Для замкнутого контура в каждый момент времени справедливо второе правило Кирхгофа, согласно которому с учетом выбранных мгновенных направлений тока и полярности ЭДС
![]() ,
(25.2)
,
(25.2)
где
Ur
= JR
= R
![]() — напряжение на общем активном
сопротивлении контура;UC
=
— напряжение на общем активном
сопротивлении контура;UC
=
![]() — напряжение на конденсаторе;
– ЭДС, создающая переменный ток в
контуре; S
= – L
— напряжение на конденсаторе;
– ЭДС, создающая переменный ток в
контуре; S
= – L
![]() – ЭДС самоиндукции в катушке.
– ЭДС самоиндукции в катушке.
Подставляя соответствующие выражения, после преобразований, получаем
![]() .
(25.3)
.
(25.3)
Поскольку при выполнении лабораторной работы, измеряемой величиной будет напряжение на конденсаторе, то перейдем в полученном уравнении к переменной UC
![]() ;
;
![]() .
.
Кроме того, введем обозначения:
![]() .
.
В результате уравнение (25.3) приобретает вид
![]() ,
(25.4)
,
(25.4)
где 0 – циклическая частота собственных незатухающих колебаний в контуре; — коэффициент затухания.
Общее решение уравнения (25.4) складывается из общего решения соответствующего однородного уравнения U1 и любого частного решения U2 неоднородного уравнения (25.4)
![]() .
.
Известно 1, что если < 0 , U1 равно
![]() ,
(25.5)
,
(25.5)
где
![]() —
частота собственных затухающих колебаний
осциллятора.
—
частота собственных затухающих колебаний
осциллятора.
Амплитуда
этих собственных колебаний
![]() зависит от начальных условий и от
времени. Со временем она становится
пренебрежимо малой и в контуре остаются
только вынужденные колеба-
нияU2
, амплитуда которых от времени не зависит.
В этом случае вынужденные колебания
называют установившимися. Для них
зависит от начальных условий и от
времени. Со временем она становится
пренебрежимо малой и в контуре остаются
только вынужденные колеба-
нияU2
, амплитуда которых от времени не зависит.
В этом случае вынужденные колебания
называют установившимися. Для них
![]() .
.
Вынужденные
колебания становятся с течением времени
установившимися и в случае, когда
выполняется обратное неравенство:
> 0.
Разница только в том, что функция
![]() уменьшается со временем апериодически.
уменьшается со временем апериодически.
Частное
решение уравнения (25.4) проще всего искать
в комплексной
форме,
заменив в его правой части cos(t)
на eit
= cos(t)
+ isin(t).
Найдя решение такого уровня в виде
комплексной функции
![]() ,
нужно взять действительную часть, т. е.Re
,
нужно взять действительную часть, т. е.Re![]() ,
которая и будет искомым решением
уравнения (25.4).
,
которая и будет искомым решением
уравнения (25.4).
Будем искать частное решение уравнения
![]() (25.6)
(25.6)
в виде
![]() .
(25.7)
.
(25.7)
Подставляя предполагаемое решение (25.7) в (25.6), получаем
![]() .
.
Сокращая
на
![]() и выражая
и выражая![]() найдем
найдем
![]() .
.
Представим знаменатель этого выражения в показательном виде
![]() .
.
Модуль этого выражения равен
![]() (25.8)
(25.8)
а аргумент определяется формулой
![]() .
(25.9)
.
(25.9)
Подставляя (25.8) и (25.9) в (25.7), найдем:
![]()
и, следовательно,
![]() .
(25.10)
.
(25.10)
В результате для установившихся вынужденных колебаний напряжения на конденсаторе получаем
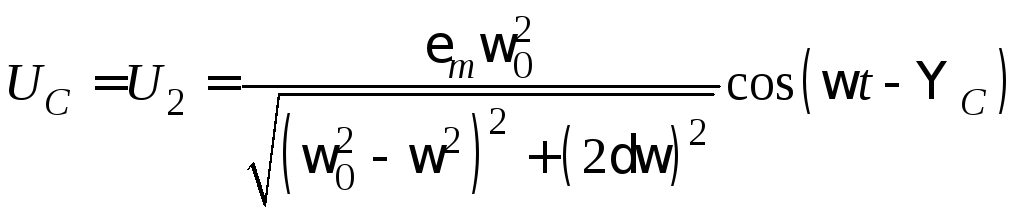 ,
(25.11)
,
(25.11)
где
![]() дает сдвиг фаз между колебаниями
напряжения на конденсаторе и колебаниям
ЭДС источника.
дает сдвиг фаз между колебаниями
напряжения на конденсаторе и колебаниям
ЭДС источника.
Из
(25.11) видно, что амплитуда вынужденных
установившихся колебаний
![]() равна
равна
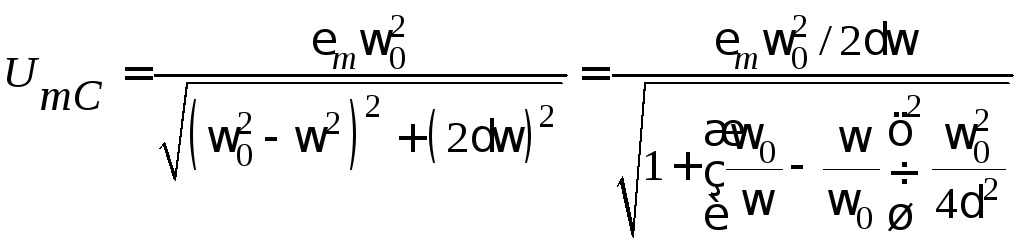 .
(25.12)
.
(25.12)
Величина
![]() при
при![]() (резонансная частота) достигает максимума,
который равен
(резонансная частота) достигает максимума,
который равен
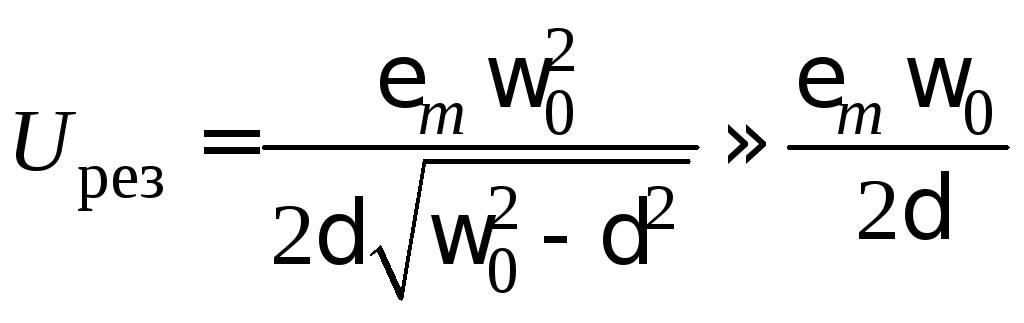 ,
(25.13)
,
(25.13)
причем
последняя формула верна при
![]()
Необходимо
отметить (проверьте это самостоятельно),
что резонансная частота колебаний
напряжения на катушке
![]() больше, чем
больше, чем![]() ,
и, следовательно, резонанс напряжения
наLC
цепочке наблюдается при промежуточной
частоте
,
и, следовательно, резонанс напряжения
наLC
цепочке наблюдается при промежуточной
частоте
![]() .
.
Уравнение
(25.12) определяет форму амплитудно-частотной
характеристики (АЧХ) колебаний на
конденсаторе, которую называют резонансной
кривой (рис. 25.2). Ширина и высота этой
кривой зависят от коэффициента
![]() Эта величина называетсядобротностью
колебательного контура
Эта величина называетсядобротностью
колебательного контура
![]() .
Физический смысл этого параметра
поясняется в лабораторной работе № 23.
.
Физический смысл этого параметра
поясняется в лабораторной работе № 23.
Итак, добротность это
![]() .
(25.14)
.
(25.14)
Последнее выражение верно при << 0.
