algebra

a31 a32 a33 a44

Следуя по стрелке, мы присваиваем элементам множеств Ai порядковые номера и тем самым строим отображение в . Элементы, встретившиеся неоднократно, конечно, пропускаются (это возможно, так как множества Ai не обязаны не пересекаться).

1.4. Теорема Кантора

Для произвольного конечного множества A из (1.1) следует неравенство A 2A . Оказывается, это неравенство справедливо и для произвольного бесконечного множества.

Теорема 1.8 (Кантор). Для произвольного множества A

A 2A .

Доказательство. Неравенство A 2A устанавливается сюръекцией x {x}.

Чтобы доказать, что A 2A , покажем, что допущение о существовании биекции : A 2A приводит к противоречию. Действительно, пусть — биекция из A в 2A. Рассмотрим множество

(множество I содержит те и только те элементы, которые не содержатся в своем образе). Так как — биективное отображение, то для любого элемента из 2A найдется прообраз в A. Пусть для I 2A таким прообразом будет некоторый

Оба раза мы приходим к противоречию, следовательно, не верно наше предположение о существовании биекции .

1.5. Несчетность множества действительных чисел

Основная задача данного раздела — доказать, что .

Теорема 1.9 (Несчетность множества ). 2 .

Доказательство. Сперва установим равномощность множеств 2 и [0, 1]. Пусть1 для любого A 2

В частности, ( ) 0), ( ) 1). Очевидно, что — сюръекция, однако, следующие примеры:

— показывают, что не является инъекцией: двум разным подмножествам множества натуральных чисел соответствует одно и то же число, или, что эквивалентно, существует [0, 1], обладающее двумя прообразами. Это возможно, если в двоичной системе счисления представимо как бесконечная дробь с периодом (1) или (0). Легко видеть, что множество N таких чисел счетно: оно есть объединение счетного числа конечных множеств, состоящих из чисел, период (1) которых начинается с первого, второго и т. д. места после запятой. Счетным является также множество M прообразов всех чисел из N (M x 2 : (x) N ). Пусть — некоторая биекция из M в N. Скорректируем теперь отображение . Для любого A 2 положим

(A) (A), если A M,

(A), если A / M.

Легко видеть, что — биекция из 2 в [0, 1]. Так как [0, 1] , то 2

.

Теперь из теоремы Кантора получаем

Утверждение 1.10. .

1 Через

мы обозначили представление действительного числа в двоичной системе счисления.

1.6. Декартово произведение

Декартовым произведением A1 A2 An множеств A1, A2, , An называется множество всех упорядоченных наборов (a1, a2, an), таких, что ai A (i 1, 2, n). Декартовой n- ой степенью An множества A называется множество всех упорядоченных наборов (a1, a2, an), таких, что ai A (i 1, 2, n).

Упражнение 1.11. Доказать, что n , n для любого натурального n.

Рис. 2.2: Равные и неравные векторы

a

b a

Рис. 2.3: Противоположные векторы

Два коллинеарных вектора, имеющих одинаковую длину и направленных в разные стороны называются противоположными. Вектор, противоположный

a, обозначается a. Таким образом, . Вектор, противоположный нулевому вектору, — это сам нулевой вектор: o o.

2.1.1. Линейные операции

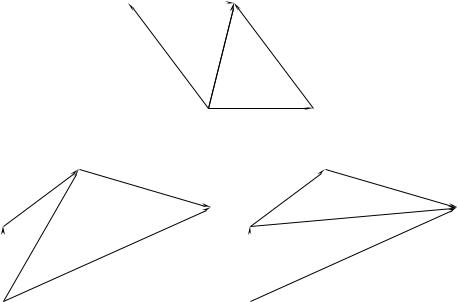
Определим операцию сложения векторов. Суммой векторов a и b называется вектор c, который можно получить, отложив вектор b из конца вектора a и соединив начало вектора a с концом b (правило треугольника). Сумма векторов a и b обозначается a b.

Другой способ найти сумму — использовать так называемое правило параллелограмма: векторы a и b откладываются из одной точки и строится паралле-

Рис. 2.4: Сумма векторов. Правило треугольника и правило параллелограмма.

Рис. 2.5:

лограмм (если векторы a и b неколлинеарны), смежные стороны которого суть a

иb. Диагональ параллелограмма, начинающаяся из начальной точки векторов a

иb очевидно есть сумма векторов a и b.

Определим операцию умножения вектора на скаляр. Пусть a — вектор, а — вещественное число (скаляр). Произведением вектора b на скаляр

называется вектор, коллинеарный вектору b, длина которого равна b , а направление совпадает с направлением вектора b, если 0, и противоположно, если 0. Произведение вектора b на скаляр обозначается b. Знак операции « » часто опускается. Если a o или 0, то считают, что a o.

Операции сложение векторов и умножения вектора на скаляр называются линейными операциями. Рассмотрим некоторые свойства этих операций.

Утверждение 2.1 (Свойства линейных операций). Для произвольных векторов a, b, c и произвольных скаляров , справедливо

1.a b b a (коммутативность сложения)

2.(a b) c a (b c) (ассоциативность сложения)

3.a o a

4.a ( a) o

5.1a a

6.( a) ( )a

Доказательство. Доказательства свойств 1, 2 понятно из рис. 2.7, 2.6. Остальные свойства очевидны.

Разумеется, здесь можно было бы упомянуть и о других свойствах линейных операций геометрических векторов, например, ( 1) a a, 0 a o и др.

b

Рис. 2.6: Доказательство коммутативности сложения геометрических векторов

Рис. 2.7: Доказательство ассоциативности сложения геометрических векторов

Почему мы остановились именно на упомянутых выше свойствах, будет ясно из дальнейшего.

Введем операцию вычитания векторов. Разностью векторов a и b называется такой вектор c, что c b a. Непосредственно можно проверить, что вектор c a ( b) удовлетворяет этому определению (c b a ( b) b a o a) и, следовательно, является разностью. Также легко видеть, что по векторам a и b их разность определяется единственным образом. Действительно, пусть векторы c и c — оба удовлетворяют определению разности. Тогда c b c b. Прибавляя к обеим частям этого равенства вектор b, получим c c .

Разность векторов a и b обозначается a b. Итак,

a b a ( b),

см. рис. 2.8. Если a и b отложены из одной начальной точки, то из рисунка видно, что a b можно изобразить как вектор, соединяющий конец вектора b с концом вектора a.

Часто удобно все векторы откладывать из одной точки , называемой в этом случае полюсом. Такие векторы называются радиус-векторами.

Если — некоторая точка, то вектор называется радиус-вектором точки . Очевидно, что если полюс фиксирован, то между множеством всех радиус-векторов и множеством всех точек (на плоскости или в пространстве) существует взаимнооднозначное соответствие. Этот факт позволяет иногда отождествлять радиус-векторы с соответствующими им точками.

b

Рис. 2.8: Разность векторов

2e2 a

e2

Рис. 2.9:

2.1.2. Базисы и аффинные системы координат

Рассмотрим два некомпланарных вектора на плоскости. Будем говорить, что они образуют базис на плоскости.

Теорема 2.2. Пусть e1, e2 образуют базис на плоскости. Тогда для любого вектора a на плоскости существуют, причем единственные, скаляры 1 и 2, такие, что

Доказательство. Существование. Отложим векторы из одной точки , см. рис. 2.9. Через конец вектора a проведем прямую параллельно вектору e2 до пересечения с прямой, на которой лежит e1. Аналогично, через конец вектора a проведем прямую параллельно вектору e1 до пересечения с прямой, на которой лежит e2. Получаем, что a 1e1 2e2 для некоторых чисел 1, 2.

Единственность. Предположим, что имеется два разложения:

a 1e1 2e2 1e1 2e2,

откуда ( 1 1)e1 ( 2 2)e2 o. Если 1 1, то

e1 2 2 e2,1 1

т. е. векторы e1 и e2 коллинеарны, что невозможно, так как они образуют базис. К аналогичному выводу приходим, предположив, что 2 2. Следовательно,1 1, 2 2, т. е. разложение по базису единственно.

Равенство (2.1) называется разложением вектора a по базису e1, e2, а скаляры 1 и 2 — координатами вектора a в базисе e1, e2.

Тот факт, что координаты вектора a в базисе e1, e2 суть 1 и 2, будем записывать следующим образом:

a( 1, 2) или [a] ( 1, 2)

или (чтобы уточнить, в каком базисе заданы координаты)

[a]e1,e2 ( 1, 2).

Теорема 2.3. Координаты суммы векторов равны сумме соответствующих координат: если [a] ( 1, 2), [b] ( 1, 2), то [a b] ( 1 1, 2 2). Координаты произведения вектора на число равны произведению координат на это число: если [a] ( 1, 2), то [ a] ( 1, 2).

Доказательство. Найдем сумму векторов a 1e1 2 и b 1e1 2e2.

Следовательно, [ a] ( 1, 2).

Совокупность некоторой фиксированной точки (полюса) и базиса e1, e2 на плоскости называется (аффинной) системой координат. При этом точка называется началом системы координат, а прямые, проходящие через параллельно базисным векторам, — ее осями. На каждой из осей задается направление, определяемое направлением соответствующего базисного вектора. Оси системы координат на плоскости традиционно называются осью абсцисс (или осью x) и осью ординат (или осью y).

Координатами точки в некоторой системе координат , e1, e2 называются координаты ее радиус-вектора:

[ ] [ ]

Имеем , поэтому координаты вектора равны координатам его конца минус координаты начала.

2.1.3. Ортонормированный базис и декартова система координат

a

Вектор длины 1 называется единичным вектором. Легко видеть, что a есть

единичный вектор, коллинеарный вектору a и соноправленный с ним.

Углом между векторами , называется величина угла . Говорят, что векторы a и b ортогональны, или перпендикулярны, есди угол между a и b

равен /2. Обозначение для ортогональных векторов: a b. Считают, что нулевой вектор ортогонален любому вектору.

Базис e1, e2 называется ортогональным, если векторы e1 и e2 ортогональны. Базис e1, e2 называется ортонормированным, если векторы e1 и e2 суть ортогональные единичные векторы. Если базис e1, e2 ортонормированный, то система