Лекция . Задачи и методы сопротивления материалов. Растяжение и сжатие.{jcomments on}

Общие понятия.

Возведение сооружений и строительство машин (которые далее будем называть конструкциями) начинается с составления проекта, в котором определяют форму, размеры и материал конструкции. Каждая конструкция составляется из отдельных деталей, взаимно соединенных между собой. Эти детали будем называть элементами конструкций. В процессе эксплуатации элементы в той или иной степени участвуют в работе и подвергаются действию различных внешних факторов: нагрузок, изменений температуры.

Под влиянием внешних сил элементы конструкций изменяют свою первоначальную геометрическую форму, объем и размеры. Такое изменение называют деформацией.

Величина деформации может при определенных условиях нарушить нормальную работу конструкции и даже оказаться опасной для целости того или иного элемента.

Для обеспечения нормальной и безопасной работы конструкция должна удовлетворять условиям прочности, жесткости и надежности.

Прочность – это способность конструкции выдерживать заданную нагрузку, не разрушаясь.

Жесткость – способность конструкции под действием внешних сил сопротивляться возникновению деформации.

Надежность – свойство конструкции выполнять заданные функции, сохраняя свои эксплуатационные показатели в определенных нормативных пределах в течение требуемого промежутка времени.

Этими вопросами и занимается наука сопротивление материалов.

Сопротивление материалов – наука, в которой изложены принципы и методы расчета элементов конструкций на прочность, жесткость и надежность.

Кроме этих требований, проектируемые сооружения должны удовлетворять требованиям наибольшей экономичности и долговечности.

 

Основные формы элементов конструкций

 

При всем разнообразии видов элементов конструкций их можно свести к сравнительно небольшому числу основных форм.

Стержень или брус – тело, у которого один размер (длина) значительно превышает два других (поперечных) размера (рис. 1).

В машиностроении встречаются стержни как прямолинейные (рис. 1, а), так и криволинейные (рис. 1, б), как постоянного (рис. 1, а), так и переменного (рис. 1, в) сечения.

Стержни, у которых толщина стенки значительно меньше габаритных размеров поперечного сечения, называют тонкостенными (рис. 1, г). В настоящее время они широко применяются в строительных конструкциях, судо- и особенно в авиастроении.

Рис. 1

Оболочка представляет собой тело, ограниченное криволинейными поверхностями, расположенными на близком расстоянии друг от друга.

Поверхность, которая делит толщину оболочки на равные части, называется срединной. По форме срединной поверхности различают оболочки цилиндрические (рис. 2, а), конические (рис. 2, б), сферические (рис. 2, в) и др. К оболочкам относятся неплоские стенки тонкостенных резервуаров, котлов, купола зданий, обшивки фюзеляжа, крыла и других частей летательных аппаратов, корпуса подводных лодок и т. д.

Если срединная поверхность представляет собой плоскость, то расчетный объект называют пластинкой (рис. 2, г). Встречаются пластинки круглые (рис. 2, д), прямоугольные (рис. 2, г) и других очертаний. К пластинкам могут быть отнесены плоские днища и крышки резервуаров, перекрытия инженерных сооружений, диски турбомашин и т. п.

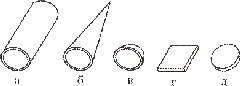
Рис. 2

Тела, у которых все три размера одного порядка, называют массивными телами. К ним относятся фундаменты сооружений, подпорные стенки и т. п.

Основные виды деформаций.

Как уже говорилось, под действием нагрузок конструкция деформируется, т. е. форма и размеры ее могут изменяться.

Деформации бывают упругие, т. е. исчезающие после прекращения действия вызвавших их сил, и пластические, или остаточные, - не исчезающие.

Деформации элементов конструкций могут быть очень сложными, но эти сложные деформации всегда можно представить состоящими из небольшого числа основных видов деформаций.

Основными видами деформаций элементов конструкций являются:

1. растяжение (рис. 3, а) или сжатие (рис. 3, б). Растяжение или сжатие возникает, например, в случае, когда к стержню по его оси приложены противоположно направленные силы.

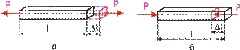
Рис. 3 

Изменение первоначальной длины стержня называют абсолютным удлинением при растяжении и абсолютным укорочением при сжатии. Отношение абсолютного удлинения (укорочения) к первоначальной длине стержня называют относительным удлинением на длине и обозначают

2. сдвиг или срез (рис. 4). Сдвиг или срез возникает, когда внешние силы смещают два параллельных плоских сечения стержня одно относительно другого при неизменном расстоянии между ними;

Рис. 4

Величина смещения называется абсолютным сдвигом. Отношение абсолютного сдвига к расстоянию между смещающимися плоскостями называют относительным сдвигом. Вследствие малости угла при упругих деформациях его тангенс принимают равным углу перекоса рассматриваемого элемента. Следовательно, относительный сдвиг

.

3. кручение (рис. 5). Кручение возникает при действии на стержень внешних сил, образующих момент относительно оси стержня;

4.

5.

Рис. 5

Деформация кручения сопровождается поворотом поперечных сечений стержня относительно друг друга вокруг его оси. Угол поворота одного сечения стержня относительно другого, находящегося на расстоянии , называют углом закручивания на длине . Отношение угла закручивания к длине называют относительным углом закручивания:

6. изгиб (рис. 6). Деформация изгиба заключается в искривлении оси прямого стержня или в изменении кривизны кривого стержня.

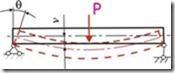
Рис. 6

В прямых стержнях перемещения точек, направленные перпендикулярно к начальному расположению оси, называют прогибами и обозначают буквой . При изгибе происходит также поворот сечений стержня вокруг осей, лежащих в плоскостях сечений. Углы поворота сечений относительно их первоначальных положений обозначают буквой .

 

Основные гипотезы науки о сопротивлении материалов.

 

Для построения теории сопротивления материалов принимают некоторые допущения (гипотезы) относительно структуры и свойств материалов, а также о характере деформации.

7. Гипотеза о сплошности материала. Предполагается, что материал сплошь заполняет форму тела. Атомическая теория дискретного состояния вещества во внимание не принимается.

8. Гипотеза об однородности и изотропности. В любом объеме и в любом направлении свойства материала считаются одинаковыми. В некоторых случаях предположение об изотропии неприемлемо. Например, свойства древесины вдоль и поперек волокон существенно различны.

9. Гипотеза о малости деформации. Предполагается, что деформации малы по сравнению с размерами тела. Это позволяет составлять уравнения статики для недеформированного тела. 

10. Гипотеза об идеальной упругости материала. Все тела предполагаются абсолютно упругими. 

Перечисленные выше гипотезы намного упрощают решение задач по расчету на прочность, жесткость и устойчивость. Результаты расчетов хорошо сходятся с данными практики.

Внутренние силы. Метод сечений.

Внутри любого материала имеются внутренние междуатомные силы, наличие которых определяет способность тела воспринимать действующие на него внешние силы, сопротивляться разрушению, изменению формы и размеров. Приложение к телу внешней нагрузки вызывает изменение внутренних сил. В сопротивлении материалов изучаются дополнительные внутренние силы. В сопротивлении материалов они называются просто внутренними силами.

Внутренние силы – силы взаимодействия между отдельными элементами конструкций или между отдельными частями элемента, возникающие под действием внешних сил.

Чтобы численно установить величину внутренних сил пользуются методом сечений.

Метод сечений сводится к четырем действиям:

1. Разрезают (мысленно) тело плоскостью в том месте, где нужно определить внутренние силы (рис. 7);

Рис. 7

2. Отбрасывают любую отрезанную часть тела (желательно наиболее сложную), а ее действие на оставшуюся часть заменяют внутренними силами, чтобы оставшаяся исследуемая часть находилась в равновесии (рис.8);

Рис. 8

3. Приводят систему сил к одной точке (как правило, к центру тяжести сечения) и проецируют главный вектор и главный момент системы внутренних сил на нормаль к плоскости (ось ) и главные центральные оси сечения ( и ).

Полученные силы (N, Qy, Qz) (рис. 9) и моменты (Мк, Мy, Mz) называют внутренними силовыми факторами в сечении

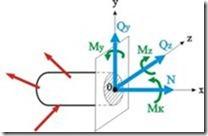
Рис. 9

Для внутренних силовых факторов приняты следующие названия:

- продольная или осевая сила;

и - поперечные силы;

- крутящий момент;

и - изгибающие моменты.

4. Находят внутренние силовые факторы, составляя шесть уравнений равновесия статики для рассматриваемой части рассеченного тела.

Напряжение

Если в сечении выделить бесконечно малую площадку и предположить, что внутренние силы, приложенные к его различным точкам, одинаковы по величине и направлению, то равнодействующая их будет проходить через центр тяжести элемента (рис. 10).

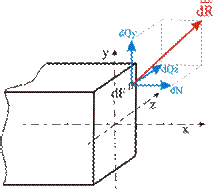
Рис. 10

Проекциями на оси , и будут элементарная продольная сила , и элементарные поперечные силы и .

Разделим эти элементарные силы на площадь , получим величины, называемые напряжениями в точке проведенного сечения.

; ; ,

где - нормальное напряжение; - касательное напряжение.

Напряжение – внутренняя сила, отнесенная к единице площади в данной точке рассматриваемого сечения.

Напряжение измеряется в единицах напряжения - паскалях (Па) и кратных ему – (кПа, МПа)

Иногда кроме нормальных и касательных напряжений рассматривают еще и полное напряжение

Понятие «напряжение» играет очень важную роль в расчетах на прочность. Поэтому значительная часть курса сопротивления материалов отводится изучению способов вычисления напряжений и .

 

Растяжение и сжатие

 

Центральным растяжением (сжатием) называется такой вид деформации, при котором в поперечном сечении бруса возникает только продольная сила (растягивающая и сжимающая) а все остальные внутренние силовые факторы равны нулю.

Растягивающие продольные силы принято считать положительными, а сжимающие – отрицательными.

Продольные силы определяются с помощью метода сечений.

Пример

Пусть имеется ступенчатый стержень, нагруженный силами , и вдоль оси стержня, показанного на рис. 11, а. Определить величину продольных сил.

Решение. Стержень может быть разделен на участки по местам приложения нагрузок и по местам изменения поперечного сечения.

Первый участок ограничен точками приложения сил и . Направим ось вдоль оси участка вверх с началом координат в точке приложения силы (начало первого участка). Мысленно рассечем первый участок поперечным сечением на расстоянии от начала первого участка. Причем координата может быть взята в интервале , где - длина первого участка.

Рассмотрим равновесие нижней части стержня, заменив действие верхней части на нижнюю часть стержня продольной силой , предварительно направив ее в сторону растяжения рассматриваемой части.

Из условия равновесия статики:

; , кН

Положительный знак продольной силы говорит о том, что первый участок растянут.

Значение продольной силы не зависит от координаты , поэтому на всем участке значение продольной силы постоянно и равно .

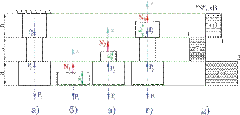
Рис. 11

Второй участок ограничен точками приложения сил и . Направим ось вдоль оси участка вверх с началом координат в точке приложения силы (начало второго участка).

Мысленно рассечем второй участок поперечным сечением на расстоянии от начала второго участка. Причем координата может быть взята в интервале , где - длина второго участка.

Рассмотрим равновесие нижней части стержня, заменив действие верхней части на нижнюю часть стержня продольной силой , предварительно направив ее в сторону растяжения рассматриваемой части.

Из условия равновесия статики:

;

, кН

Знак минус говорит о том, что второй участок сжат.

Аналогично для третьего участка :

;

, кН

Полученные результаты для большей наглядности удобней представить в виде графика (эпюры N), показывающего изменение продольной силы вдоль оси стержня. Для этого проводим нулевую (базовую) линию параллельно оси стержня, перпендикулярно которой будем в масштабе откладывать значения осевых усилий (рис. 1.11, д). В одну сторону откладываем положительные значения, в другую - отрицательные. Эпюра заштриховывается перпендикулярно нулевой линии, а в нутрии эпюры ставится знак откладываемой величины. Рядом указываются значения откладываемых величин. Рядом с эпюрой в кавычках указывается название эпюры («N») и через запятую - единицы измерения (кН)

 

Нормальные напряжения

 

Отсутствие поперечных сил при растяжении (сжатии) дает основание предположить, что в каждой точке поперечного сечения касательные напряжения равны нулю.

Продольная сила в сечении бруса является равнодействующей нормальных напряжений, действующих в плоскости поперечного сечения.

Закон распределения напряжений может быть определен из эксперимента. Установлено, что если на стержень нанести прямоугольную сетку, то после приложения продольной нагрузки вид сетки не изменится, она по-прежнему останется прямоугольной, а все линии прямыми. Поэтому можно сделать вывод о равномерном по сечению распределении продольных деформаций и перейти к гипотезе плоских сечений.

Гипотеза плоских сечений: поперечные сечения стержня, плоские и нормальные к его оси до деформации остаются плоскими и нормальными к оси и при деформации.

Так как одинаковым удлинениям соответствуют одинаковые напряжения, то напряжения всех волокон в поперечном сечении будут одинаковы. Тогда

,

откуда

Отметим, что полученное выражение справедливо для сечений достаточно удаленных от мест приложения сосредоточенных нагрузок. Вблизи приложения нагрузок распределение напряжений носит сложный характер.

Для обеспечения прочности стержня должно выполняться условие прочности - конструкция будет прочной, если максимальное напряжение ни в одной точке нагруженной конструкции не превышает допускаемой величины, определяемой свойствами данного материала и условиями работы конструкции, то есть

.

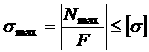Допускаемое напряжение

,

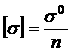где - опасное напряжение;

- коэффициент запаса прочности. Величина коэффициента запаса прочности назначается в пределах , а иногда и более, с учетом многих факторов, в частности, точности принятых расчетных соотношений, условий эксплуатации конструкции, особых требований по безопасности работы, норм, принятых в отрасли промышленности. В машинах и аппаратах химических производств .

Испытания механических свойств материалов

 

 

Для определения опасных напряжений необходимо провести испытания образцов материала на растяжение и сжатие (более подробно эта тема рассмотрена в методических указаниях к лабораторным работам по сопротивлению материалов (1 часть)»

Испытания материалов на растяжение (сжатие) заключается в построении кривых зависимостей между величиной удлинения (укорочения) и величиной силы , которая вызвала данное удлинение (укорочение). От диаграммы растяжения в координатах и можно, разделив все ординаты на площадь поперечного сечения образца , а абсциссы на первоначальную длину образца , перейти к диаграмме в координатах и , где:

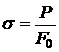- нормальное напряжение в поперечном сечении образца;

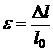- относительное удлинение

Диаграмма - более удобна и лучше отражает физические свойства материала, так как она не зависит от геометрических размеров испытываемого образца.

Рассмотрим характерные точки диаграммы - растяжения малоуглеродистой стали (рис. 12, кривая 1), которые характеризуют прочность исследуемого материала. Данная диаграмма называется диаграммой условных напряжений, так как напряжения определяются отношением силы на первоначальную площадь поперечного сечения.

Диаграмма истинных напряжений (рис. 12, кривая 2) в диапазоне напряжений, соответствующих характеристикам прочности, мало отличается от диаграммы условных напряжений, поэтому на практике используют диаграммы условных напряжений.

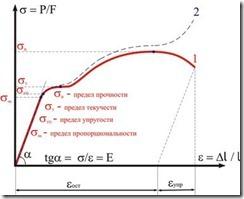
Рис. 12 Диаграммы растяжения в координатах - .

До определенного значения напряжения имеет место линейная зависимость между величинами относительного удлинения и напряжения . Материал в данном случае подчиняется закону Гука – закону пропорциональности нагрузки и деформации.

,

где коэффициент пропорциональности - модуль продольной упругости(модуль Юнга), величина которого постоянна для каждого материала. Он характеризует жесткость материала, т.е. способность сопротивляться деформированию под действием внешней нагрузки..

Максимальное напряжение , до которого материал подчиняется закону Гука, называется пределом пропорциональности.

Выше предела пропорциональности наблюдается нелинейная зависимость напряжения от относительной деформации.

До какого то значения напряжения после снятия нагрузки материал все еще не имеет остаточных деформаций.

Наибольшее напряжение , до которого остаточная деформация при разгрузке не обнаруживается, называется пределом упругости.

Предел упругости является характеристикой, не связанной с законом Гука. Предел упругости может иметь значение как выше, так и ниже значения предела пропорциональности. Эти напряжения близки друг к другу и обычно различием между ними пренебрегают.

При каком то значении напряжения удлинение образца растет при практически постоянном значении растягивающей силы. Такой процесс деформации называется текучестью материала.

Наименьшее напряжение , при котором деформация образца происходит при постоянном растягивающем усилии, называется пределом текучести.

Для металлов, не имеющих площадки текучести, предел текучести определяют условно как напряжение, при котором остаточная деформация составляет 0,2 %.

После стадии текучести материал вновь приобретает способность увеличивать сопротивление дальнейшей деформации.

Напряжение, соответствующее максимальной нагрузке , которую может воспринимать образец, называется пределом прочности или временным сопротивлением.

После достижения максимального усилия при дальнейшем растяжении образца деформация происходит, главным образом, на небольшой длине образца. Это ведет к образованию местного сужения в виде шейки и к падению силы (рис. 12. кривая 1), несмотря на то, что истинное напряжение в сечении шейки непрерывно растет (рис. 12. кривая 2).

Полное удлинение, полученное образцом перед разрушением, уменьшится после разрыва, так как в частях образца исчезнут упругие деформации.

Отношение в процентах приращения расчетной длины образца после разрыва к его первоначальной длине , называется относительным остаточным удлинением :

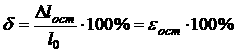
Отношение в процентах абсолютного уменьшения площади поперечного сечения в шейке к первоначальной площади , называется относительным остаточным сужением.:

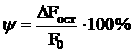
Относительное остаточное удлинение и относительное остаточное сужение являются характеристиками пластичности материала.

Испытание на сжатие, несмотря на простоту, проводят реже, так как модуль упругости , предел упругости и предел текучести при сжатии примерно те же, что и при растяжении.

Испытанию на сжатие подвергают главным образом хрупкие материалы, которые, как правило, лучше сопротивляются сжатию, чем растяжению, и применяются для изготовления элементов, работающих на сжатие.

Подробное описание испытания на сжатие описано в методических указаниях к лабораторным работам по дисциплине «Сопротивление материалов» (первая часть).

 

Деформации при растяжении (сжатии)

 

При растяжении стержня постоянного поперечного сечения длина увеличивается, а поперечные размеры уменьшаются (рис. 13).

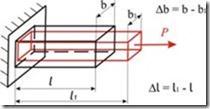
Рис. 13

Из закона Гука

Учитывая то, что и имеем:

Если на рассматриваемом участке продольная сила и поперечное сечение переменны, то удлинение участка длиной получим, суммируя удлинения бесконечно малых участков.

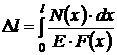
где - координата бесконечно малого участка;

- продольная сила в сечении с координатой ;

- длина бесконечно малого участка;

- площадь поперечного сечения стержня с координатой .

Если мы возьмем произвольный поперечный размер , то его изменение, отнесенное к его первоначальному значению, даст нам относительную поперечную деформацию (рис. 13):

Между поперечной и продольной относительной деформацией при простом растяжении (сжатии) в пределах применимости закона Гука существует постоянное отношение. Абсолютная величина этого отношения носит название Коэффициента Пуассона и обозначается буквой :

Учитывая, что продольная и поперечная деформация всегда имеют противоположные знаки, получаем

Коэффициент Пуассона наряду с модулем продольной упругости характеризует упругие свойства материалов.

В некоторых случаях для обеспечения нормальной работы конструкций размеры их элементов нужно выбирать так, чтобы обеспечивалось условие жесткости. При растяжении (сжатии) условие жесткости имеет следующий вид:

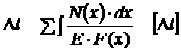
где - изменение размеров детали;

- допускаемая величина этого изменения.

Расчет по условию жесткости всегда следует дополнять расчетом на прочность.

Лекция 2. Геометрические характеристики плоских сечений{jcomments on}

Основным объектом, изучаемым в курсе сопротивление материалов, является стержень.

Сопротивление стержня различным видам деформации часто зависит не только от его материалов и размеров, но и от очертаний оси, формы поперечных сечений и их расположения. Рассмотрим основные геометрические характеристики поперечных сечений бруса, определяющие сопротивление различным видам деформаций.

Статические моменты площади. Центр тяжести площади.

Рассмотрим произвольную фигуру (поперечное сечение бруса), связанную с координатными осями и (рис. 2.1). Выделим элемент площади с координатами , . По аналогии с выражением для момента силы относительно какой-либо оси можно составить выражения и для момента площади, которое называется моментом площади. Так, произведение элемента площади на расстояние от оси .

(2.1)

называется статическим моментом элемента площади относительно оси .

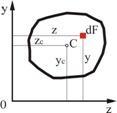
Рис. 2.1

Аналогично:

(2.2)

 

Просуммировав такие произведения по всей площади фигуры, получим соответственно статические моменты относительно осей и :

; (2.3)

 

Пусть , - координаты центра тяжести фигуры. Продолжая аналогию с моментами сил, на основании теоремы о моменте равнодействующей можно написать следующие выражения:

(2.4)

 

где - площадь фигуры. Очевидно, что статические моменты площади относительно осей проходящих через центр тяжести (центральных осей) равны нулю.

Координаты центра тяжести:

. (2.5)

В качестве примера вычислим статический момент треугольника (рис. 2.2) относительно оси, проходящей через основание. На расстоянии от нее выделим элементарную площадку в виде полоски, параллельной оси . Площадь полоски

.

Учитывая, что

,

имеем

. 

 

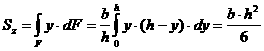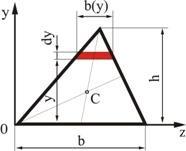
Рис. 2.2 

Еще проще решить эту задачу, пользуясь формулой (2.4).

Учитывая, что

; ,

статический момент

Для вычисления статических моментов сложной фигуры ее разбивают на простые части (рис. 2.3), для каждой из которых известна площадь и положение центра тяжести и . Статический момент площади всей фигуры относительно данной оси определяется как сумма статических моментов каждой части:

Рис. 2.3 

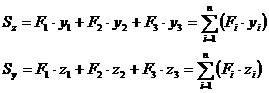(2.6)

 

 

По формулам (2.5) и (2.6) легко найти координаты центра тяжести сложной фигуры:

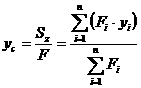; (2.7)

Моменты инерции плоски фигур

Осевым, или экваториальным, моментом инерции площади фигуры называют интеграл произведений элементарных площадей на квадраты расстояний от рассматриваемой оси

(2.8)

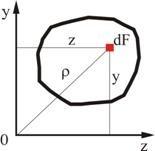
Рис. 2.4

 

Полярным моментом инерции площади фигуры относительно данной точки (полюса ) называют интеграл произведений элементарных площадей на квадраты их расстояний от полюса:

(2.9)

Если через полюс проведена система взаимно перпендикулярных осей и , то . Из выражения (2.9) имеем

(2.10)

Отметим, что величины осевых и полярных моментов инерции всегда положительны.

Центробежным моментом инерции называют интеграл произведений площадей элементарных площадок на их расстояния от координатных осей и :

(2.11)

В зависимости от положения осей центробежный момент инерции может быть положительным или отрицательным. Очевидно, что, постепенно поворачивая оси, можно найти такое их положение, при котором центробежный момент инерции равен нулю. Такие оси называют главными осями инерции.

Две взаимно перпендикулярные оси, из которых хотя бы одна является осью симметрии фигуры, всегда будут ее главными осями инерции

Главные оси, проходящие через центр тяжести сечения, называют главными центральными осями.

Лекция 3. Основы теории напряженного состояния.{jcomments on}