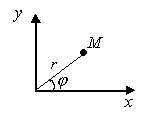
1.7.3. Кривые второго порядка в полярной системе координат.
Под
полярной системой координат будем
понимать луч (координатную ось ОХ),
исходящий из полюса в т.О. Полярными
координатами, определяющими точку М в
полярной системе координат, будут
расстояние от полюса до т. М (ОМ=r)
и угол между радиус-вектором
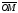и осью
.
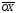Переход от ПСК к ДСК осуществляется по
формулам
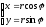(1.7.27)
Примем т.F – фокус линии второго порядка, за полюс полярной системы координат и выразим эксцентриситет по единой для всех линий второго порядка формуле:
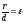(1.7.28)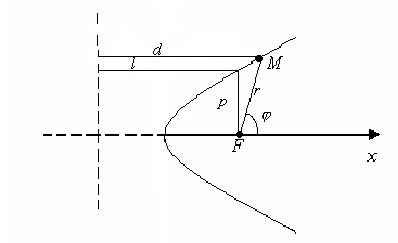
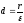(1.7.29)
;
;
;
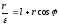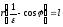т.к
;
;
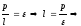
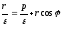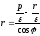проделанные преобразования позволяют получить формулу
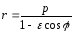(1.7.30)
– представляющую собой общее уравнение прямых второго порядка полярной системе координат
Лекция 8
1.8 Аналитическая геометрия в пространстве.
1.8.1. Уравнение плоскости в пространстве.
1.8.2. Уравнение прямой линии в пространстве.
1.8.3. Поверхности 2-го порядка.
1.8.1 . Уравнение плоскости в пространстве.
Определение 1.8.1.
Под плоскостью будем понимать поверхность, обладающую тем свойством, что, нормаль, проведённая к данной поверхности, перпендикулярна к любому вектору целиком принадлежащему к данной поверхности.
1) Каноническое уравнение плоскости.
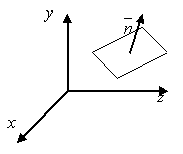
В ДСК плоскость в пространстве описывается уравнением первого порядка:
Аx + By + Cz + D = 0 (1.8.1)
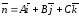(1.8.2)
2)Уравнение плоскости, проходящей через 3 точки.
М(x,y,z)
P
z
М2(x2,y2,z2)
M1(x1,y1,z1)
М3(x3,y3,z3)
0
у
х
=
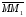(х-х1)i
+ (у-у1)j
+ (z-z1)
k
M2M1
= (x2-x1)i
+ (y2-y1)j
+ (z2-z1)k
M3M1
=(x3-x1)i
+ (y3-y1)j
+
(z3-z1) k
MM1
· M2M1
· M3M1
= 0 - по условию компланарности , смешанное
произведение векторов = 0 , откуда:
x-x1
y-y1 z-z1
x2-x1 y2-y1 z2-z1 = 0 (1.8.3)
x3-x1 y3-y1 z3-z1
3)Угол между двумя плоскостями.
Угол между двумя плоскостями равен углу между перпендикулярами, проведёнными к данным плоскостям. Пусть плоскость Р1 определена уравнением А1х + В1у + С1z = D1 и, вектор N1 = А1i + В1j + С1k, а плоскость Р2 определена уравнением А2х + В2у + С2z = D2 и вектор N2 = А2i + В2j + С2k. Тогда, исходя из скалярного произведения векторов, косинус угла между этими нормалями будет иметь вид:
.
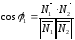(1.8.4)
Следовательно, косинус угла между плоскостями находится по формуле:
,
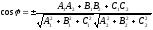(1.8.5)
а по косинусу находится и сам угол.
4) Условия параллельности и перпендикулярности плоскостей.
Для того, чтобы плоскости были перпендикулярны необходимо и достаточно, чтобы косинус угла между плоскостями равнялся нулю. Это условие выполняется, если:
.
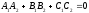(1.8.6)
Если плоскости
параллельны, то векторы нормалей
коллинеарны:
.
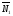
Это условие выполняется, если:.
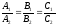(1.8.7)