2.1.1. Действительные числа. Абсолютная величина действительного числа. Постоянные и переменные величины.

1. Действительное число.

Целые и дробные, положительные и отрицательные числа вместе числом нуль называются рациональными числами.

Числа, представленные бесконечными непериодическими десятичными дробями называются иррациональными числами.

Совокупность всех рациональных и иррациональных чисел называется множеством действительных (или вещественных) чисел

Геометрическим аналогом действительного числа служит числовая ось. На протяжении двух разделов: дифференциального и интегрального исчислений мы будем иметь дело только с областью действительных чисел.

2. Абсолютная величина действительного числа.

Абсолютной величиной действительного числа называется

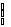
|a|= (2.1.1.)

3) Свойства абсолютной величины.

1 |a а (2.1.2.)

Доказательство:

   если   

   если       

2 b    b (2.1.3.)

Доказательство:

А) Пусть   b  b  b



bb

b+bb|a|+|bb 

Б) Пусть a+b < 0|a+b|= - (a+b)= - a-b

|a|  - a

|b|  - b

|a|+|b|a-b= - (a+b) = |a+b  |a+b |   b 

Из  и  a  b  |a|+|b| (ч.т.д.)

3 |a-b|  a|-|b| (2.1..4.)

Доказательство:

Пусть a – b = c  |a -b |= |c|

a = b+c |a |= |b+c|  |b |+|c | |a |-|b || c| = |a-b| a|-|b| |a-b| (ч.т.д.)

4 |ab| = |a| |b| (2.1.5.)

5 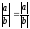(2.1.6)

4) Постоянные и переменные величины

Величина называется постоянной, если ее численное значение не меняется. Величина называется переменной, если ее численное значение меняется. Переменные величины, которые только возрастают или только убывают, называются монотонными. Переменная величина Х называется ограниченной, если существует такое постоянное число М>О, что все значения переменной величины удовлетворяют условию -ММ.

Типовые примеры

1.

Решение:

х 0 исключается из рассмотрения, так как в этом случае < 0, что противоречит свойству 1)) в скобках.

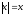
Итак х 0. При х 0 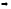х-3 0 х 3.

2.

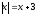
Решение:

х 0 исключается из рассмотрения, так как в этом случае х=х+3, или 0=3, что противоречит здравому смыслу.

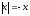
Итак х 0. При х 0 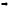-х= х+3 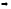х=-1,5.

2.1.2. Функция. Область определения функции. Основные элементарные функции.

1. Понятие функции.

Переменная величина yназывается функцией переменной величиныxєD, если каждому значениюxиз областиDсоответствует определенное значение величиныy. При этомxназывают независимой переменной или аргументом, аy– зависимой – или функцией.

2. Область существования (определения) и изменения функции.

Областью существования функции называется такая область изменения аргумента х, в которой функция y определена.

Областью изменения функции называется такая область значений функции y, которую она принимает при всех значениях переменной x из области существования.

3. Основные элементарные функции:

• степенная: у=х^а а є R (действительное число),

• показательная: у=а^х а >0, a ≠ 1,

• логарифмическая: у=log_ax, а >0, a ≠ 1,

• тригонометрическая: y = sin x, y=cosx, y=tgx, y=ctgx,

• обратная тригонометрическая: y =arc sin x, y=arccosx, y=arctgx, y=arcctgx.

Элементарной называется функция, составленная из конечного числа основных элементарных функций и постоянных чисел с помощью конечного числа арифметических действий и взятия функции от функции.

Типовой пример.

Определить область существования функции .

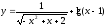Решение:

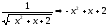> 0 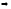- 2 < х < 2,

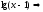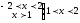х – 1 > 0, х>1, . Ответ: 1 < х < 2.