
5 Linear inequalities. In plane. Bundle of lines.
By
analogy with that a linear equation represents a line on a plane, a
linear inequality
 determines a half-plane (the set of points the coordinates of which
determines a half-plane (the set of points the coordinates of which and
and satisfy this inequality) restricted by the line
satisfy this inequality) restricted by the line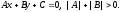 Show that this assertion is true for the case when a line
Show that this assertion is true for the case when a line divide a plane
divide a plane into two half-planes denoted by
into two half-planes denoted by and
and :
:
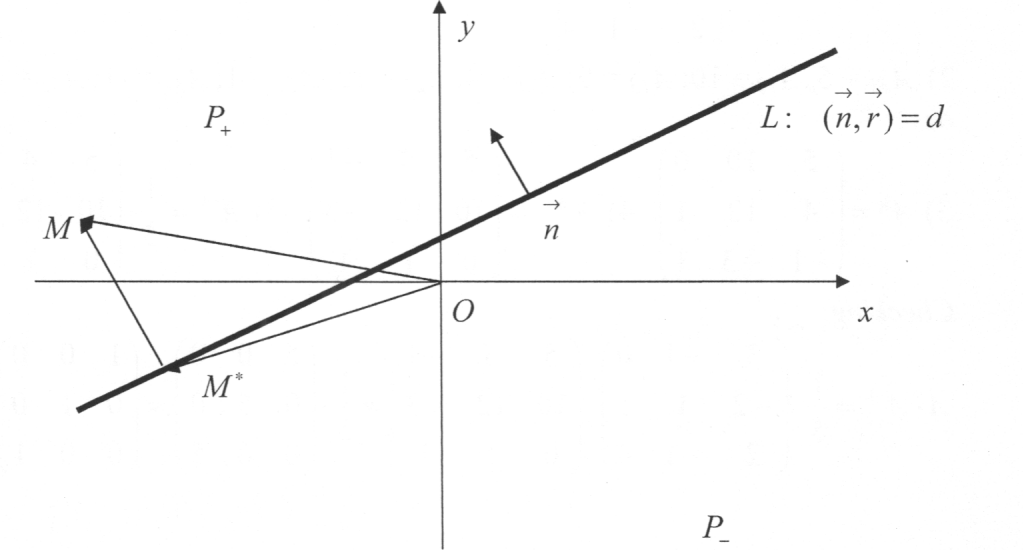
We
say that a point
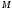 with radius-vector
with radius-vector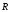 belongs to the half-plane
belongs to the half-plane (or respectively
(or respectively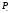 )
if there exists
)
if there exists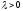 (respectively
(respectively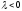 )
such that
)
such that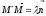 where
where is
the orthogonal projection of
is
the orthogonal projection of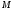 on
the line
on
the line .
.
Theorem
5.
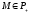 iff
iff
Proof:
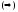 Let
Let ,
i.e. there is
,
i.e. there is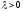 such that
such that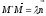 .
Estimate the quantity
.
Estimate the quantity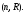 Since
Since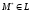 ,
, and
then
and
then
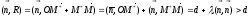 by
positivity of
by
positivity of
 .
.
 Let
Let
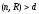 and
and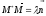 .
Then by
.
Then by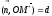 we obtain
we obtain
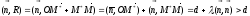 .
.
Then
since
 ,
we have
,
we have and consequently
and consequently .
.
Exercise
1.
The system of coordinates
 on a plane and a line
on a plane and a line with equation
with equation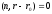 are given. Find the distance between this line and a point
are given. Find the distance between this line and a point the radius-vector of which is
the radius-vector of which is .
.
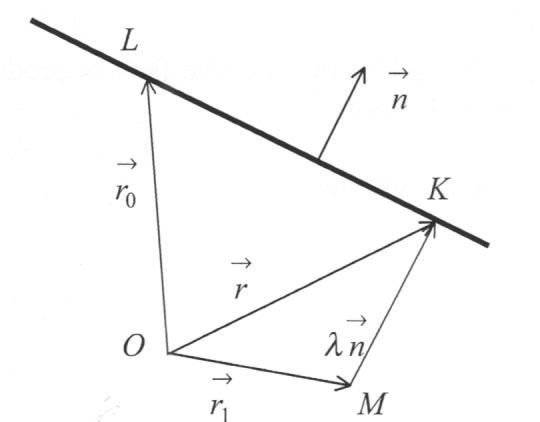
Solution:
Let
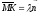 .
Then
.
Then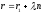 .
The point
.
The point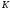 belongs to this line, therefore the following holds:
belongs to this line, therefore the following holds: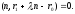 Consequently,
Consequently,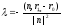 .
.
Substituting
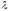 in the expression for
in the expression for ,
we obtain
,
we obtain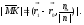
Let
the system of coordinates be orthonormal. For an equation
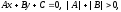 as showed the vector
as showed the vector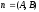 is perpendicular to the line. Therefore,
is perpendicular to the line. Therefore,
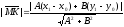 .
.
Taking
in account that the point
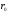 lies on the line
lies on the line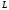 and consequently
and consequently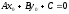 ,
we can write the final answer in the form:
,
we can write the final answer in the form: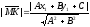 .
.
A bundle of lines on a plane is called the set of all lines passing through some given point named the vertex of the bundle.
Theorem
6.
Let a point that is common for all lines of a bundle is the point of
intersection of non-parallel lines
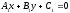 and
and .
Then
.
Then
1.
For any line of the bundle there is a pair of non-simultaneously
equal to zero numbers
 and
and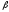 such that
such that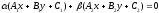 is an equation of this line.
is an equation of this line.
2.
For any non-simultaneously equal to zero numbers
 and
and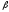 the equation
the equation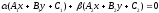 is an equation of some line of this bundle.
is an equation of some line of this bundle.
Proof:
1. Take some point
 non-coinciding with the vertex of the bundle and assume
non-coinciding with the vertex of the bundle and assume
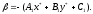 Observe
that
Observe
that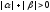 since the point
since the point doesn’t belong to these lines simultaneously. Moreover, the line
doesn’t belong to these lines simultaneously. Moreover, the line

passes
through both the point
 and the vertex of the bundle, and consequently it belongs to the
bundle.
and the vertex of the bundle, and consequently it belongs to the
bundle.
2.
Let
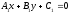 and
and be a pair of intersecting lines from the considered bundle. Then
obviously
be a pair of intersecting lines from the considered bundle. Then
obviously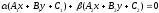 .
And the equation
.
And the equation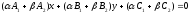 is an equation of a line because from
is an equation of a line because from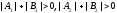 and
and follows that
follows that
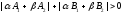 .
.
Indeed,
assume the contrary:
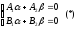 .
.
The
lines
 and
and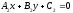 by construction have at least one common point. Therefore they either
coincide or are intersected. By Theorem 4 they are coinciding iff
by construction have at least one common point. Therefore they either
coincide or are intersected. By Theorem 4 they are coinciding iff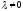 for which
for which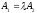 and
and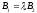 .
The last two equalities are equivalent to
.
The last two equalities are equivalent to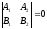 .
.
In
the considered case the lines are intersected, therefore
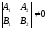 and consequently the system (*) can have only one solution. On other
hand, obviously that this system has a trivial solution
and consequently the system (*) can have only one solution. On other
hand, obviously that this system has a trivial solution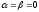 ,
but it contradicts to the inequality
,
but it contradicts to the inequality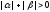 .
.
An
equation
 with non-simultaneously equal to zero parameters
with non-simultaneously equal to zero parameters and
and is called anequation
of a bundle of lines
on a plane.
is called anequation
of a bundle of lines
on a plane.
6. Plane in the space. Plane in the space
Let
a system of coordinates
 in the space and a plane
in the space and a plane passing through a point
passing through a point with lying on it non-collinear vectors
with lying on it non-collinear vectors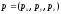 and
and be given. Vectors
be given. Vectors and
and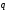 are calleddirecting
vectors
of the plane
are calleddirecting
vectors
of the plane
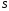 .
.
Theorem
1.
The set of radius-vectors of points on plane
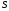 is represented in the form
is represented in the form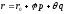 where
where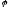 and
and are arbitrary real parameters.
are arbitrary real parameters.

Proof:
Let
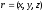 be some point on the plane. Then vectors
be some point on the plane. Then vectors and
and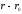 will be coplanar.
will be coplanar.
Whence
we obtain
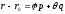 and consequently an equation of the plane will have the form:
and consequently an equation of the plane will have the form:
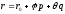 where
where
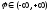 and
and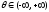 .
.
Theorem 2. Every plane in any Cartesian system of coordinates can be represented by an equation:

Proof:
The condition of coplanarity of vectors
 ,
,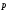 and
and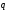 in the coordinate form has the form:
in the coordinate form has the form:
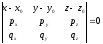 .
.
Whence
 ,
or finally
,
or finally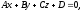 where
numbers
where
numbers
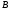 and
and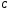 are equal to:
are equal to: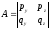 ;
;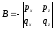 ;
;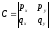 ,
and
,
and .
Thus, we obtained that an equation of plane is an equation of the
first degree.
.
Thus, we obtained that an equation of plane is an equation of the
first degree.
The
condition of non-simultaneous equality of numbers

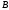 and
and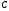 to zero follows by non-collinearity of vectors
to zero follows by non-collinearity of vectors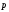 and
and .
.
Theorem
3.
Every equation of the form
 in any Cartesian system of coordinates is an equation of some plane.
in any Cartesian system of coordinates is an equation of some plane.
Proof:
By
direct checking we are convinced that
 in case
in case
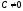 can be written in the form:
can be written in the form: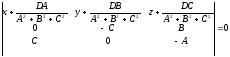 ,
and in case
,
and in case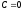 in the form:
in the form: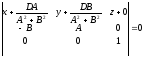 .
.
In both cases these equations determine a plane passing through some given point and that is parallel to two non-collinear vectors.
Theorem
4.
Planes
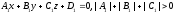 and
and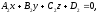
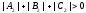 are
parallel iff their principal vectors are collinear.
are
parallel iff their principal vectors are collinear.
Proof:
 If principal vectors are collinear then there is such a number
If principal vectors are collinear then there is such a number that
that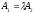 ,
, ,
,
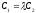 and the system of equations
and the system of equations
 can be rewritten in the form
can be rewritten in the form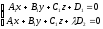 .
If
.
If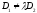 ,
there is no common point of these planes; if
,
there is no common point of these planes; if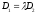 ,
all points are common that means parallelism of the planes.
,
all points are common that means parallelism of the planes.
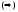 Let
the planes
Let
the planes
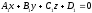 and
and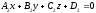 be parallel. Then they must intersect the same coordinate planes by
parallel lines.Let
for definiteness these coordinate planes are planes for which
be parallel. Then they must intersect the same coordinate planes by
parallel lines.Let
for definiteness these coordinate planes are planes for which
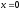 and
and .
Lines of intersection corresponding to the first of the coordinate
planes will be determined by the following systems of equations:
.
Lines of intersection corresponding to the first of the coordinate
planes will be determined by the following systems of equations:
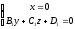 and
and
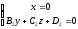 .
.
Parallelism
of these lines means an existence of
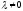 such that
such that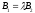 ,
,
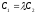 .
.
Considering
the case
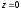 ,
we obtain the analogous system of equations:
,
we obtain the analogous system of equations:
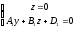 and
and
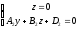 .
.
But
the condition
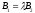 and parallelism of this pair of lines imply that
and parallelism of this pair of lines imply that
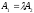 .
.
Corollary
2.
The equations
 and
and
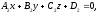
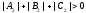
are
equations of the same plane iff there exists
 such that
such that
 ,
,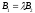 ,
,
 ,
,
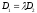 .
.
A bundle of planes in the space is called the set of all planes passing through a given line.
An
equation
of a bundle of planes
passing through a line determined by intersection of a pair of
non-parallel planes
 and
and
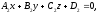
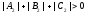
is called the equation of the form
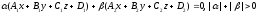 .
.
A sheaf of planes in the space is called the set of all planes passing through a given point.
If
a point
 belonging simultaneously to three planes
belonging simultaneously to three planes
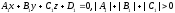
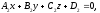
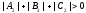 and
and
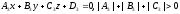
is unique then an equation of the form
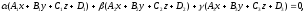
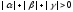 is
called an equation
of a sheaf of planes
passing through the point
is
called an equation
of a sheaf of planes
passing through the point
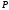 .
.
