
16-20матан
.docx16) Екінші текті қисық сызықты интегралдың жолдан тәуелсіздігі.
1. Екінші текті қисық сызықты интегралдың интегралдау жолынан тәуелсіздігі туралы теорема (дәлелдеуімен).
2. Екі айнымалыдан тәуелді фунцияны толық дифференциалы бойынша тұрғызу (формуласын жазу).


17) Бірінші текті беттік интеграл.
1. Бірінші текті беттік интеграл анықтамасы.
2. Бірінші текті беттік интеграл қасиеттері.
3. Бірінші текті беттік интегралды есептеу.
Шекарасы
құрама-жатық
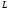 контуры болатын құрама-жатық
контуры болатын құрама-жатық
 бетінің нүктелерінде анықталған
бетінің нүктелерінде анықталған
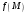 функциясы берілсін. Оны құрама-жатық
қисықтармен
функциясы берілсін. Оны құрама-жатық
қисықтармен
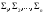 бөліктерге бөлшектейік те, бұлардың
әрқайсысының ауданына
сәйкес
бөліктерге бөлшектейік те, бұлардың
әрқайсысының ауданына
сәйкес
 арқылы белгілейік. Әрбір бөліктен кез
келген
арқылы белгілейік. Әрбір бөліктен кез
келген
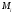 нүктесін алып,
нүктесін алып,
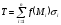 қосындысын
түзейік. Мұны
қосындысын
түзейік. Мұны
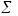 бетінің осы бөліктеуге және
бетінің осы бөліктеуге және
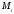 нүктелерінің осылай таңдап алынуына
сәйкес
нүктелерінің осылай таңдап алынуына
сәйкес
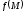 функциясының интегралдық қосындысы
деп атаймыз. Егер
функциясының интегралдық қосындысы
деп атаймыз. Егер
 бетінің
бетінің
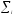 бөліктері диаметрлерінің ең үлкені
нөлге ұмтылғанда
бөліктері диаметрлерінің ең үлкені
нөлге ұмтылғанда
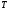 интегралдық қосындысы белгілі бір
ақырлы шекке ұмтылса, онда бұл шек
интегралдық қосындысы белгілі бір
ақырлы шекке ұмтылса, онда бұл шек
 функциясының
функциясының
 беті бойынша бірінші
текті беттік интеграл
деп аталады және
беті бойынша бірінші
текті беттік интеграл
деп аталады және
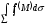 арқылы белгіленеді
арқылы белгіленеді
1-теорема.
Айталық,
 жатық беті
жатық беті
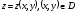 теңдеуі арқылы берілсін (мұндағы
теңдеуі арқылы берілсін (мұндағы
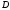 -
тұйық шектеулі аймақ), ал
-
тұйық шектеулі аймақ), ал
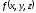 осы
осы
 бетінде анықталған шектеулі функция
болсын. Онда
бетінде анықталған шектеулі функция
болсын. Онда
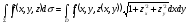 теңдігі орынды әрі мұның оң жағындағы
екі еселі интеграл бар болса, онда сол
жағындағы беттік интеграл да бар.
теңдігі орынды әрі мұның оң жағындағы
екі еселі интеграл бар болса, онда сол
жағындағы беттік интеграл да бар.
Бірінші текті беттік интеграл қасиеттері
Егер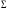 беті жатық, ал f(x,y,z) функциясы бұл бетте
үзіліссіз болса, онда
беті жатық, ал f(x,y,z) функциясы бұл бетте
үзіліссіз болса, онда

беттік интегралы бар.
Шынында да (32)-нің оң жағындағы интеграл астындағы функция үзіліссіз, демек, ол бар. Сондықтан оның сол жағындағыбеттік интеграл да бар.
2-теорема. Егер параметрлік

теңдеуі
арқылы берілген жатық бет, ал
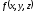 осы бетте анықталған шектеулі функция
болса, онда
осы бетте анықталған шектеулі функция
болса, онда
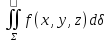
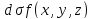 =
= (40)
(40)
мұндағы
 ,
,
 ,
,
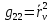
Егер (32)-нің оң жағындағы екі еселі интеграл бар болса, онда сол жағындағы беттік интеграл да бар.
Бірінші текті беттік интегралды есептеу
Айталық,
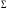 жатық беті
жатық беті
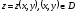 теңдеуі арқылы берілсін (мұндағы
теңдеуі арқылы берілсін (мұндағы
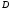 -
тұйық шектеулі аймақ), ал
-
тұйық шектеулі аймақ), ал
 осы
осы
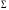 бетінде анықталған шектеулі функция
болсын. Онда
бетінде анықталған шектеулі функция
болсын. Онда
 (32)
(32)
теңдігі орынды әрі мұның оң жағындағы екі еселі интеграл бар болса, онда сол жағындағы беттік интеграл да бар.
Дәлелдеу
үшін бетін
құрама-жатыққисықтармен
бетін
құрама-жатыққисықтармен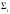
 бөліккебөлеміз.
Бұлбөліктерді
бөліккебөлеміз.
Бұлбөліктерді жазықтығынапроекциялап,
жазықтығынапроекциялап,
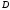 аймағыныңсәйкес
аймағыныңсәйкес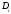 бөліктеуіналамыз
(сурет).
Сондаәрбір
бөліктеуіналамыз
(сурет).
Сондаәрбір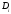 элементтерініңдиаметрісәйкес
элементтерініңдиаметрісәйкес диаметріненаспайтыныайқын.
Енді
диаметріненаспайтыныайқын.
Енді

беттік интегралына сәйкес
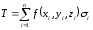 (33)
(33)
интегралдық
қосындысын қарастырайық.
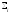 элементінің
элементінің
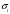 ауданын
ауданын

түрінде
өрнектеп (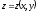 беті
жатық, демек,
беті
жатық, демек,
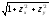 -
үзіліссіз функция), бұл екі еселі
интегралға орта мән туралы теореманы
қолданып, мұны
-
үзіліссіз функция), бұл екі еселі
интегралға орта мән туралы теореманы
қолданып, мұны
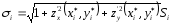
түрінде
жазамыз. Мұндағы
 нүктесі
нүктесі
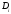 аймағының анықталған белгілі нүктесі,
ал
аймағының анықталған белгілі нүктесі,
ал
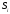 осы аймақ ауданы. Сонда (33) интегралдық
қосындыны былай
осы аймақ ауданы. Сонда (33) интегралдық
қосындыны былай
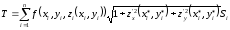 (34)
(34)
жазуға
болады. Енді мұны
 бетінің
дәл сол бөліктеуіне сәйкес (32) оң
жағындағы екі еселі интегралдың
бетінің
дәл сол бөліктеуіне сәйкес (32) оң
жағындағы екі еселі интегралдың
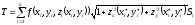 (35)
(35)
интегралдық
қосындысымен салыстырамыз. Бұл екі
қосындының бірінен бірінің өзгешелігі
тек
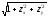 функциясының әртүрлі нүктелердегі
мәндерінде: (34) интегралды қосындыда
функциясының әртүрлі нүктелердегі
мәндерінде: (34) интегралды қосындыда
 мәні
мәні
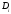 элементінің орта мән теоремасы беретін
элементінің орта мән теоремасы беретін
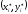 нүктесінде
де, ал (35) интегралдық қосындыда бұл
нүктесінде
де, ал (35) интегралдық қосындыда бұл
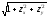 функциясының
функциясының
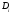 элементінен қалауымызша алынған
элементінен қалауымызша алынған
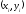 нүктесіндегі мәні, әрине, жалпы
жағдайда, бұл нүктелер тең емес.
нүктесіндегі мәні, әрине, жалпы
жағдайда, бұл нүктелер тең емес.
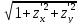 функциясы
үзіліссіз, демек, тұйық шектеулі D
аймағында бірқалыпты үзіліссіз, сондықтан
кез келген ε
функциясы
үзіліссіз, демек, тұйық шектеулі D
аймағында бірқалыпты үзіліссіз, сондықтан
кез келген ε
 үшін
үшін
 саны табылып,
саны табылып,
 аймақтары диаметрлерінің ең үлкені
аймақтары диаметрлерінің ең үлкені
 санынан кіші болғанда
санынан кіші болғанда
 <
ε (36)
<
ε (36)
Ал теорема шарты бойынша f(x,y,z) шектеулі, яғни
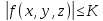 =const,
=const,
сондықтан (36) бағалаудан

 .
(37)
.
(37)
18) Екінші текті беттік интеграл.
1. Екінші текті беттік интеграл анықтамасы.
2. Екінші текті беттік интеграл қасиеттері.
3. Екінші текті беттік интегралды есептеу.




Екінші
текті беттік интегралды анықтау үшін
бізге ең алдымен бет жақтарының ұғымы
қажет. Егер
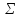 бетінде жатқан және оның шекарасымен
ортақ нүктесі жоқ кезкелген тұйық контур
бойымен жүріп өткенде бет нормалі
бағытын өзгертпесе
бетінде жатқан және оның шекарасымен
ортақ нүктесі жоқ кезкелген тұйық контур
бойымен жүріп өткенде бет нормалі
бағытын өзгертпесе
 екі жақты бет деп аталады. Егер бойымен
жүріп өткен бет нормалы бағытын кері
өзгертетін бетте жатқан тұйық контур
табылса, онда бет бір
жақты бет
деп аталады.
екі жақты бет деп аталады. Егер бойымен
жүріп өткен бет нормалы бағытын кері
өзгертетін бетте жатқан тұйық контур
табылса, онда бет бір
жақты бет
деп аталады.
Жатық регуляр бет бағытталатын бет деп аталады,егер оның бойымен бірлік нормаль векторлар үзіліссіз өрісін таңдау мүмкін болса,егер ондай мүмкіндік жоқ болса, онда бет бағытталмайтын бет деп аталады. Бірлік нормаль векторларының үзіліссіз өрісі таңдап алынған бет бағытталған бет деп аталады.
19) Беттік интегралдың кейбір қолданыстары.
1. Геометриядағы кейбір қолданыстары.
2. Физикадағы кейбір қолданыстары.

Мысалы:

20) Остроградский-Гаусс формуласы, Стокс формуласы.
1. Остроградский-Гаусс формуласы.
2. Стокс формуласы.
Айталық,
D-тұйық жәй xoy жазықтығында жатқан L
контурының іші болсын,
 .
R
.
R кеңістігінде тұйық аймақ
V={(x,y,z):z
кеңістігінде тұйық аймақ
V={(x,y,z):z (x,y)
(x,y)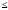 z
z z
z (x,y),
(x,y)
(x,y),
(x,y)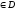 }
(z
}
(z (x,y)
(x,y) z(x,y),(x,y)
z(x,y),(x,y) D)
қарастырайық.Тұйық
V аймағы
D)
қарастырайық.Тұйық
V аймағы
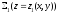 және
және
 беттері
мен жасаушылары
L контурының нүктелері арқылы өтетін
OZ өсіне параллель
беттері
мен жасаушылары
L контурының нүктелері арқылы өтетін
OZ өсіне параллель
 цилиндрлік бүйір бетімен қоршалған деп
ұйғарамыз. Мұндай аймақты oxy жазықтығы
арқылы қарапайым аймақ деп атаймыз. Дәл
осылай oyz, ozx жазықтықтары арқылы да
қарапайым аймақтарды анықтауға болады.
Егер V аймағын әр жазықтық бойынша
қарапайым аймақтарға жіктеу мүмкін
болса, онда оны жай ғана қысқаша қарапайым
аймақ деп атайтын боламыз.
цилиндрлік бүйір бетімен қоршалған деп
ұйғарамыз. Мұндай аймақты oxy жазықтығы
арқылы қарапайым аймақ деп атаймыз. Дәл
осылай oyz, ozx жазықтықтары арқылы да
қарапайым аймақтарды анықтауға болады.
Егер V аймағын әр жазықтық бойынша
қарапайым аймақтарға жіктеу мүмкін
болса, онда оны жай ғана қысқаша қарапайым
аймақ деп атайтын боламыз.
 бетін
сыртқы бірлік нормаль векторлары арқылы,
яғни n=(cos(n,x), cos(n,y), cos(n,z)) векторы арқылы
бағыттаймыз, демек,
бетін
сыртқы бірлік нормаль векторлары арқылы,
яғни n=(cos(n,x), cos(n,y), cos(n,z)) векторы арқылы
бағыттаймыз, демек,
 бетінің
сыртқы жағын қарастырамыз.
бетінің
сыртқы жағын қарастырамыз.
теорема.
Егер V-қарапайым аймақ, яғни барлық
координаттық жазықтықтар арқылы
қарапайым аймақ, ал P, Q, R функциялары
өздерінің
 туындыларымен
бірге осы V тұйық аймағында үзіліссіз
болса, онда Остроградский формуласы
деп аталатын
туындыларымен
бірге осы V тұйық аймағында үзіліссіз
болса, онда Остроградский формуласы
деп аталатын
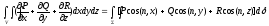 (1)
(1)
формула орынды.
Дәлелдеуі. V аймағында анықталған және z бойынша туындысы осы аймақта үзіліссіз R(x,y,z) функциясы үшін жүргіземіз. Егер
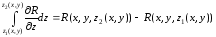 айқын
теңдеуін, V кеңістік аймағының (x,y)
жазықтығындағы проекциясы D аймағы
бойынша интегралдасақ, онда
айқын
теңдеуін, V кеңістік аймағының (x,y)
жазықтығындағы проекциясы D аймағы
бойынша интегралдасақ, онда

 (2)
(2)
Оң
жақтағы интегралдардың біріншісін
z=z (x,y)
бетінің жоғарғы жағы бойынша R(x,y,z)
функциясынан алынған беттік интеграл
түрінде жазуға болады:
(x,y)
бетінің жоғарғы жағы бойынша R(x,y,z)
функциясынан алынған беттік интеграл
түрінде жазуға болады: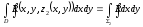 Дәл
осылай оң жақтағы екінші интегралды
R(x,y,z) функциясынан
Дәл
осылай оң жақтағы екінші интегралды
R(x,y,z) функциясынан
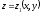 бетінің жоғарғы жағы бойынша алынған
беттік интеграл немесе кері таңбамен
алынған
бетінің жоғарғы жағы бойынша алынған
беттік интеграл немесе кері таңбамен
алынған
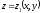 бетінің
төменгі жағы бойынша алынған беттік
интеграл түрінде жазуға болады:
бетінің
төменгі жағы бойынша алынған беттік
интеграл түрінде жазуға болады:
 Сонда
Сонда (3)
(3)
мұнда
оң жақтағы интегралдардың біріншісі
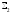 бетінің жоғарғы жағы бойынша,
ал екіншісі
бетінің жоғарғы жағы бойынша,
ал екіншісі
 бетінің төменгі жағы бойынша алынған
(3) формуланың оң жағына нөлге тең
бетінің төменгі жағы бойынша алынған
(3) формуланың оң жағына нөлге тең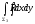
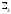 бүйір беттің сыртқы жағы бойынша алынған
интегралын қоссақ (өйткені бұл бетте
бүйір беттің сыртқы жағы бойынша алынған
интегралын қоссақ (өйткені бұл бетте
 ),
V аймағын қоршайтын
),
V аймағын қоршайтын
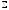 бетінің сырты бойынша алынған интегралға
келеміз. Сонымен,
бетінің сырты бойынша алынған интегралға
келеміз. Сонымен,
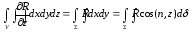 (4)Бұл
теңдік саны ақырлы координаттық
жазықтықтар арқылы қарапайым болатын
кез келген V аймағы үшін де орынды.
Шынында да, V-ны
(4)Бұл
теңдік саны ақырлы координаттық
жазықтықтар арқылы қарапайым болатын
кез келген V аймағы үшін де орынды.
Шынында да, V-ны
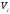 бөліктерге бөліп, олардың әрқайсысы
үшін (4) теңдікті жазып, қосындыласақ,
онда сол жағында V аймағы бойынша алынған
үш еселі интегралды, ал оң жағында
бөліктерге бөліп, олардың әрқайсысы
үшін (4) теңдікті жазып, қосындыласақ,
онда сол жағында V аймағы бойынша алынған
үш еселі интегралды, ал оң жағында
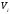 бөліктері бойынша екі рет алынған
интегралдар қосындысынан тұрады және
ол интегралдар бір рет беттің бір жағы
бойынша, ал екінші рет екінші жағы
бойынша алынады да, оларды қосындылағанда
бірін бірі жояды. Сонымен біз
бөліктері бойынша екі рет алынған
интегралдар қосындысынан тұрады және
ол интегралдар бір рет беттің бір жағы
бойынша, ал екінші рет екінші жағы
бойынша алынады да, оларды қосындылағанда
бірін бірі жояды. Сонымен біз
 (5)теңдігін
аламыз. Дәл осылай
(5)теңдігін
аламыз. Дәл осылай
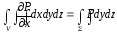 ,
,
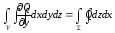 (6)теңдіктерін
де дәлелдейміз.(5) және (6) теңдіктерін
қосып,
(6)теңдіктерін
де дәлелдейміз.(5) және (6) теңдіктерін
қосып,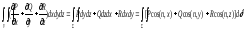
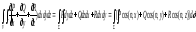 (7)Остроградский
формуласын аламыз. Теорема дәлелденді.
(7)Остроградский
формуласын аламыз. Теорема дәлелденді.
Стокс формуласы
Егер
P(x,y,z), Q(x,y,z), R(x,y,z) функциялары
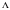 контурымен қоршалған бағытталған
контурымен қоршалған бағытталған
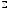 беті
жататын аймақта анықталған және біріші
ретті туындыларымен бірге осы аймақта
үзіліссіз болса,онда Стокс формуласы
деп аталатын
беті
жататын аймақта анықталған және біріші
ретті туындыларымен бірге осы аймақта
үзіліссіз болса,онда Стокс формуласы
деп аталатын
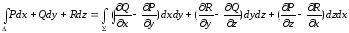 (1)
(1)
формуласы орынды.
Дәлелдеу. Алдымен интегралдың оң жағын былай
 (2)түрінде
жазып, мұның бірінші қосылғышын жеке
қарастырайық.Айталық,
(2)түрінде
жазып, мұның бірінші қосылғышын жеке
қарастырайық.Айталық,
 беті Декарт координаттарында
беті Декарт координаттарында теңдеуі
арқылы берілсін.
теңдеуі
арқылы берілсін.
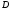 арқылы
арқылы
 бетінің
бетінің
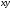 жазықтығына проекциясын және
жазықтығына проекциясын және
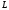 арқылы оның шекарасын, яғни
арқылы оның шекарасын, яғни
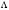 контурының проекциясын белгілейік
(суретті қараңыз).Біз
контурының проекциясын белгілейік
(суретті қараңыз).Біз
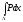 қисықсызықты интегралын қарастырып,
кеңістік
қисықсызықты интегралын қарастырып,
кеңістік
 контурының
контурының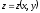 теңдеуімен берілген
теңдеуімен берілген
 бетінде жатқандығынан оны
бетінде жатқандығынан оны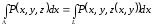 жазықтық
жазықтық
 контуры бойынша алынған қисық сызықты
интегралға түрлендіреміз. Сонан соң
Грин формуласын қолданып оны
контуры бойынша алынған қисық сызықты
интегралға түрлендіреміз. Сонан соң
Грин формуласын қолданып оны

 аймағы бойынша алынған екі еселі
интегралда келтірtміз. Мұнда
аймағы бойынша алынған екі еселі
интегралда келтірtміз. Мұнда
 функциясының x
және y
айнымалыларының күрделі функциясы
екенін және оның yбойынша
туындыны есептеуде ескердік. Нормальдік
бағыттаушы косинустары өрнектерін
пайдаланып,
функциясының x
және y
айнымалыларының күрделі функциясы
екенін және оның yбойынша
туындыны есептеуде ескердік. Нормальдік
бағыттаушы косинустары өрнектерін
пайдаланып,
 теңдігін
аламыз, сонда
теңдігін
аламыз, сонда
 Енді
Енді
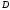 бойынша екі еселі интегралынан
бойынша екі еселі интегралынан
 бойынша интегралына көшеміз:
бойынша интегралына көшеміз:
 .Сонымен,
.Сонымен,
 (3)
(3)
Біз
формуланы табуда
 беті
беті
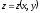 түрінде берілген деп ұйғардық. Дәл
осындай нәтижеге
түрінде берілген деп ұйғардық. Дәл
осындай нәтижеге
 бетінің
бетінің
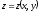 теңдеуі
арқылы берілген жағдайында да жетуге
болады. Ол үшін
теңдеуі
арқылы берілген жағдайында да жетуге
болады. Ол үшін
 бетінің
бетінің
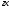 жазықтығына
(
жазықтығына
( жазықтығына емес) проекциясын қарастырып,
дәл жоғарыдағыдай дәлелдеу жүргізуге
болады. Ал, егер
жазықтығына емес) проекциясын қарастырып,
дәл жоғарыдағыдай дәлелдеу жүргізуге
болады. Ал, егер
 өсіне перпендикуляр жазықтық бөлігі
болса (әрине, онда ондай
өсіне перпендикуляр жазықтық бөлігі
болса (әрине, онда ондай
 бетті
бетті
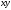 жазықтығына да,
жазықтығына да,
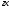 жазықтығына
да бірмәнді проекциялауға болмайды),
онда (3) түрдегі теңдік мардымсыз түрде
орынды (тривиальным образом): оның оң
жағы да, сол жағы да нөлге тең. Енді Грин
және Остроградский формулаларын
дәлелдеуде қолданған стандарттық әдіс
әрқайсысында (3) формула орындалатын
саны ақырлы беттерге жіктелетін
жазықтығына
да бірмәнді проекциялауға болмайды),
онда (3) түрдегі теңдік мардымсыз түрде
орынды (тривиальным образом): оның оң
жағы да, сол жағы да нөлге тең. Енді Грин
және Остроградский формулаларын
дәлелдеуде қолданған стандарттық әдіс
әрқайсысында (3) формула орындалатын
саны ақырлы беттерге жіктелетін
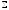 беті үшін де орынды. Сонымен, (3) теңдіктің
дұрыстығы жоғарыда келтірілген беттер
түріндегі саны ақырлы беттер кесектері
үшін де орынды екен. Сонымен, дәл
жоғарыдағы (3) теңдік сияқты дәлелденетін
беті үшін де орынды. Сонымен, (3) теңдіктің
дұрыстығы жоғарыда келтірілген беттер
түріндегі саны ақырлы беттер кесектері
үшін де орынды екен. Сонымен, дәл
жоғарыдағы (3) теңдік сияқты дәлелденетін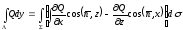 ,(4)
,(4)
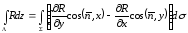 (5)теңдіктерін
аламыз. Бұл (3)-(5) теңдіктерді қосып,
дәлелдеу керек
(5)теңдіктерін
аламыз. Бұл (3)-(5) теңдіктерді қосып,
дәлелдеу керек

(2) формуланы аламыз. Міне осы формуланы Стокс формуласы деп атайды. Кейде Стокс формуласы деп (1) формулаyы да айтады.
