Глава 8

Нарушение гипотез основной линейной модели

1. Обобщенный метод наименьших квадратов (взвешенная регрессия)

Пусть нарушена гипотеза g4 и матрица ковариации ошибок по наблюдени- ям равна не σ²I_N , а σ²Ω, где Ω — вещественная симметричная положительно полуопределенная матрица (см. Приложение A.1.2), т.е. ошибки могут быть кор- релированы по наблюдениям и иметь разную дисперсию. В этом случае обычные МНК-оценки параметров регрессии (7.26) остаются несмещенными и состоятель- ными, но перестают быть эффективными в классе линейных несмещенных оценок.

Ковариационная матрица оценок МНК в этом случае приобретает вид

M_a = σ^{2 .}Z^tZ^.−1 Z^tΩZ ^.Z^tZ^.−1 .

Действительно, a − E (a) = a − α = (Z^rZ)⁻¹ Z^rε, поэтому

E ^.(a − E(a)) (a − E(a))^r. = (Z^rZ)⁻¹ Z^rE (εε^r) Z (Z^rZ)⁻¹ =

= σ² (Z^rZ)⁻¹ Z^rΩZ (Z^rZ)⁻¹ .

(Ср. с выводом формулы (7.28), где Ω = σ²I .)

258 Глава 8. Нарушение гипотез основной линейной модели

e

Обычная оценка ковариационной матрицы s² (Z^tZ)⁻¹ при этом является сме- щенной и несостоятельной. Как следствие, смещенными и несостоятельными ока- зываются оценки стандартных ошибок оценок параметров (7.35): чаще всего они преуменьшаются (т.к. ошибки по наблюдениям обычно коррелированы положи- тельно), и заключения о качестве построенной регрессии оказываются неоправ- данно оптимистичными.

По этим причинам желательно применять обобщенный МНК (ОМНК), заклю- чающийся в минимизации обобщенной остаточной дисперсии

1

e^tΩ⁻¹e.

N

В обобщенной остаточной дисперсии остатки взвешиваются в соответствии со структурой ковариационной матрицы ошибок. Минимизация приводит к полу- чению следующего оператора ОМНК-оценивания (ср. с (7.13), где Ω = I_N ):

a = (Z^tΩ⁻¹Z)⁻¹Z^tΩ⁻¹X. (8.1)

Для обоснования ОМНК проводится преобразование в пространстве наблю- дений (см. параграф 6.4) с помощью невырожденной матрицы D размерности N × N , такой, что D⁻¹D^t−1 = Ω (такое представление допускает любая ве-

щественная симметричная положительно определенная матрица, см. Приложение

A.1.2):

DX = DZα + Dε. (8.2)

Такое преобразование возвращает модель в «штатную» ситуацию, поскольку новые остатки удовлетворяют гипотезе g4:

E(Dεε^tD^t) = Dσ²ΩD^t = σ²DD⁻¹D^t−1D^t = σ²I_N .

Остаточная дисперсия теперь записывается как вания — как a = (Z^tD^tDZ)⁻¹Z^tD^tDX .

1

e^tD^tDe, а оператор оцени-

N

Что и требовалось доказать, поскольку D^tD = Ω⁻¹.

Обычно ни дисперсии, ни тем более ковариации ошибок по наблюдениям не из- вестны. В классической эконометрии рассматриваются два частных случая.

2. Гетероскедастичность ошибок

Пусть ошибки не коррелированы по наблюдениям, и матрица Ω (а вслед за ней и матрица D) диагональна. Если эта матрица единична, т.е. дисперсии ошибок

8.2. Гетероскедастичность ошибок 259

одинаковы по наблюдениям (гипотеза g4 не нарушена), то имеет место гомос- кедастичность или однородность ошибок по дисперсии — «штатная» ситуация. В противном случае констатируют гетероскедастичность ошибок или их неодно- родность по дисперсии.

i

Пусть var(ε_i) = σ² — дисперсия ошибки i-го наблюдения. Гомоскедастич-

i

ность означает, что все числа σ²

одинаковы, а гетероскедастичность — что среди

них есть несовпадающие.

Факт неоднородности остатков по дисперсии мало сказывается на качестве оце- нок регрессии, если эти дисперсии не коррелированы с независимыми факторами. Это — случай гетероскедастичности «без негативных последствий».

Данное утверждение можно проиллюстрировать в случае, когда в матрице Z все- го один столбец, т.е. n = 1 и свободный член отсутствует. Тогда формула (7.33) приобретает вид:

 ^ _{σ2 2} 

E(s²) = ¹

 _σ2

i ^zi

i _.

_{e N} 

_i − ^ _z2 ^

_{i i} i

i

Если ситуация штатная и σ² = σ² , то правая часть этой формулы преобразуется к ви-

ду ^{N − 1} σ² , и ^N s²

оказывается несмещенной оценкой σ² , как и было пока-

N N − 1 ^e

1 ^

i

зано в параграфе 7.2. Если σ_i и z_i не коррелированы, то, обозначив σ² =

N

можно утверждать, что

σ² ,

i

^ _σ2 2

2^ 2

_i z^,_i σ

z

i  _{2 ≈}

i

i

_z,_i

_z = σ ,

_{i  2} 2

i

i

т.е. ситуация остается прежней. И только если σ_i и z_i положительно (или отрица- тельно) коррелированы, факт гетероскедастичности имеет негативные последствия.

^ _σ2 2

Действительно, в случае положительной корреляции

i ^zi

z

 ₂

i

> σ² и, следова-

тельно, E

 _{N 2}

s

N − 1 ^e

< σ² . Обычная «несмещенная» оценка остаточной диспер-

сии оказывается по математическому ожиданию меньше действительного значе-

ния остаточной дисперсии, т.е. она (оценка остаточной дисперсии) дает основания для неоправданно оптимистичных заключений о качестве полученной оценки модели.

Следует заметить, что факт зависимости дисперсий ошибок от независимых факторов в экономике весьма распространен. В экономике одинаковыми по диспер-

^{сии скорее являются относительные (ε}z ^{), а не абсолютные (ε) ошибки. Поэтому,}

когда оценивается модель на основе данных по предприятиям, которые могут иметь

260 Глава 8. Нарушение гипотез основной линейной модели

и, как правило, имеют различные масштабы, гетероскедастичности с негативными последствиями просто не может не быть.

Если имеет место гетероскедастичность, то, как правило, дисперсия ошибки связана с одной или несколькими переменными, в первую очередь — с факторами регрессии. Пусть, например, дисперсия может зависеть от некоторой перемен- ной y_i , которая не является константой:

_σ2

_i = σ²

(y_i), i = 1, . . . , N.

Как правило, в качестве переменной y_i берется один из независимых факторов или математическое ожидание изучаемой переменной, т.е. x⁰ = Zα (в качестве его оценки используют расчетные значения изучаемой переменной Za).

В этой ситуации желательно решить две задачи: во-первых, определить, имеет ли место предполагаемая зависимость, а во-вторых, если зависимость обнаружена, получить оценки с ее учетом. При этом могут использоваться три группы методов. Методы первой группы позволяют работать с гетероскедастичностью, которая за-

дается произвольной непрерывной функцией σ²(·). Для методов второй группы функция σ²(·) должна быть монотонной. В методах третьей группы функция σ²(·)

предполагается известной с точностью до конечного числа параметров.

Примером метода из первой группы является критерий Бартлетта, который заключается в следующем.

Пусть модель оценена и найдены остатки e_i, i = 1, . . . , N . Для расчета b^c — статистики, лежащей в основе применения этого критерия, все множество наблю- дений делится по какому-либо принципу на k непересекающихся подмножеств. В частности, если требуется выявить, имеется ли зависимость от некоторой пе- ременной y_i, то все наблюдения упорядочиваются по возрастанию y_i, а затем в соответствии с этим порядком делятся на подмножества. Пусть

k

N_l — количество элементов в l-м подмножестве,

_s2

^ N_l = N ;

l=1

_l — оценка дисперсии остатков в l-м подмножестве, найденная на основе

остатков e_i ;

k

^{1 } N_ls²

b_s =

N

l=1

l

— отношение средней арифметической дисперсий к сред-

. _k

s

³ 2N_l

l

^.1/_N

l=1

ней геометрической; это отношение в соответствии со свойством мажорантности средних (см. п. 2.2) больше или равно единице, и чем сильнее различаются диспер- сии по подмножествам, тем оно выше.

8.2. Гетероскедастичность ошибок 261

e

2

i

s

2

2

s

s

2 ₂

1 ₄

s

2

s

2 5

3 _yi

Рис. 8.1

Тогда статистика Бартлетта равна

b^c = ^N

_k

1 1

ln b_s.

₁₊ l=1 _Nl ⁻ _N

3(k − 1)

При однородности наблюдений по дисперсии (нулевая гипотеза) эта статистика

χ

распределена как ²

k−1

. Проверка нулевой гипотезы проводится по обычному ал-

горитму.

Если нулевую гипотезу отвергнуть не удалось, т.е. ситуация гомоскедастична, то исходная оценка модели удовлетворительна. Если же нулевая гипотеза отверг- нута, то ситуация гетероскедастична.

Принцип построения статистики Бартлетта иллюстрирует рисунок 8.1.

Классический метод второй группы заключается в следующем. Все наблюдения упорядочиваются по возрастанию некоторой переменной y_i. Затем оцениваются две вспомогательные регрессии: по K «малым» и по K «большим» наблюдениям (с целью повышения мощности критерия средние N − 2K наблюдения в расчете не участвуют, а K можно, например, выбрать равным приблизительно трети N ).

Пусть s² — остаточная дисперсия в первой из этих регрессий, а s² — во второй.

1 2

В случае гомоскедастичности ошибок (нулевая гипотеза) отношение двух дисперсий

распределено как

2

_s2

s

₂ ^{∼ F}K−n−1,K−n−1^.

1

Здесь следует применять обычный F -критерий. Нулевая гипотеза о гомос- кедастичности принимается, если рассчитанная статистика превышает 95%-ный квантиль F -распределения.

262 Глава 8. Нарушение гипотез основной линейной модели

e

2

i

s

2

2

s

2

1 _yi

Рис. 8.2

Такой подход применяется, если ожидается, что дисперсия может быть только по- ложительно коррелирована с переменной y_i . Если неизвестно, положительно или отрицательно коррелирована дисперсия с рассматриваемым фактором, то следу- ет отклонять нулевую гипотезу как при больших, так и при малых значениях ста-

_s2

₂

тистики ^s2

1

. Можно применить следующий прием: рассчитать статистику как

1

отношение максимальной из дисперсий s²

и s²

к минимальной. Такая статисти-

2

ка будет иметь усеченное F -распределение, где усечение происходит на уровне медианы, и берется правая половина распределения. Отсюда следует, что для до- стижения, например, 5%-го уровня ошибки, следует взять табличную критиче- скую границу, соответствующую, 2.5%-му правому хвосту обычного (не усеченного) F -распределения. Если указанная статистика превышает данную границу, то нуле- вая гипотеза о гомоскедастичности отвергается.

Данный метод известен под названием метода Голдфельда—Квандта.

2

Можно применять упрощенный вариант этого критерия, когда дисперсии s² и

_s2 2 2

₂ считаются на основе остатков из проверяемой регрессии. При этом s₁ и s₂ не

будут независимы, и их отношение будет иметь F -распределение только прибли-

женно. Этот метод иллюстрирует рисунок 8.2.

Для того чтобы можно было применять методы третьей группы, требуется обладать конкретной информацией о том, какой именно вид имеет гетероскеда- стичность.

Так, например, если остатки прямо пропорциональны значениям фактора (n = 1):

x = zα + β + zε,

и ε удовлетворяет необходимым гипотезам, то делением обеих частей уравнения на z ситуация возвращается в «штатную»:

^x = α + ¹ β + ε,

Z Z

2. Гетероскедастичность ошибок 263

e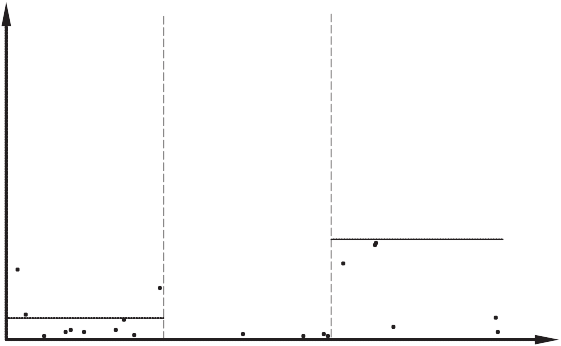

2

i

s

2

2

s

2

1 _yi

Рис. 8.3

в которой, правда, угловой коэффициент и свободный член меняются местами. Тем самым применяется преобразование в пространстве наблюдений такое, что диаго-

^{нальные элементы матрицы D равны 1}z_i ^.

Если зависимость дисперсии от других переменных известна не точно, а только с точностью до некоторых неизвестных параметров, то для проверки гомоскеда- стичности следует использовать вспомогательные регрессии.

Так называемый метод Глейзера состоит в следующем. Строится регрессия модулей остатков |e_i| на константу и те переменные, которые могут быть коррели- рованными с дисперсией (например, это может быть все множество независимых факторов или какое-то их подмножество). Если регрессия оказывается статисти- чески значимой, то гипотеза гомоскедастичности отвергается.

Построение вспомогательной регрессии от некоторой переменной y_i показано на рисунке 8.3.

i

Другой метод (критерий Годфрея) использует аналогичную вспомогательную регрессию, в которой в качестве зависимой переменной используются квадраты остатков e².

Если с помощью какого-либо из перечисленных критериев (или других анало- гичных критериев) проверены различные варианты возможной зависимости и ну- левая гипотеза во всех случаях не была отвергнута, то делается вывод, что ситуа- ция гомоскедастична или гетероскедастична без негативных последствий и что для оценки параметров модели можно использовать обычный МНК. Если же нуле- вая гипотеза отвергнута и поэтому, возможно, имеет место гетероскедастичность с негативными последствиями, то желательно получить более точные оценки, учи- тывающие гетероскедастичность.

Это можно сделать, используя для оценивания обобщенный МНК (см. уравне- ние (8.2)). Соответствующее преобразование в пространстве наблюдений состоит

264 Глава 8. Нарушение гипотез основной линейной модели

в том, чтобы каждое наблюдение умножить на d_i , т.е. требуется оценить обычным методом наименьших квадратов преобразованную регрессию с переменными d_iX_i и d_iZ_i. При этом не следует забывать, что если матрица факторов Z содержит свободный член, то его тоже нужно умножить на d_i , поэтому вместо свободного члена в регрессии появится переменная вида (d₁, . . . , d_N ). Это приводит к тому, что стандартные статистические пакеты выдают неверные значения коэффициен- та детерминации и F -статистики. Чтобы этого не происходило, требуется поль- зоваться специализированными процедурами для расчета взвешенной регрессии. Описанный метод получил название взвешенного МНК, поскольку он равнозначен

N

минимизации взвешенной суммы квадратов остатков

^ d²e² .

i i

i=1

Чтобы это можно было осуществить, необходимо каким-то образом получить оценку матрицы D, используемой для преобразования в пространстве наблюдений. Перечисленные в этом параграфе методы дают возможность не только проверить гипотезу об отсутствии гетероскедастичности, но и получить определенные оценки матрицы D (возможно, не очень хорошие).

Если S² — оценка матрицы σ²Ω , где S² — диагональная матрица, состав- ленная из оценок дисперсий, то S⁻¹ (матрица, обратная к ее квадратному кор- ню) — оценка матрицы σD.

Так, после проверки гомоскедастичности методом Глейзера в качестве диа-

гональных элементов матрицы S⁻¹ можно взять ^1

^c , где |e_i|^c — расчетные

|e_i|

l

значения |e_i|. Если используются критерии Бартлетта или Голдфельда—Квандта, то наблюдения разбиваются на группы, для каждой из которых есть оценка дис- персии, s². Тогда для этой группы наблюдений в качестве диагональных элементов

^{матрицы S−1 можно взять 1}s_l ^.

В методе Голдфельда—Квандта требуется дополнительно получить оценку дис- персии для пропущенной средней части наблюдений. Эту оценку можно получить непосредственно по остаткам пропущенных налюдений или как среднее (s² +s²)/2.

1 2

Если точный вид гетероскедастичности неизвестен, и, как следствие, взвешенный МНК неприменим, то, по крайней мере, следует скорректировать оценку ковариа- ционной матрицы оценок параметров, оцененных обычным МНК, прежде чем про- верять гипотезы о значимости коэффициентов. (Хотя при использовании обычного МНК оценки будут менее точными, но как уже упоминалось, они будут несмещенны- ми и состоятельными.) Простейший метод коррекции состоит в замене неизвестной

ковариационной матрицы ошибок σ²Ω на ее оценку S² , где S² — диагональная

i

матрица с типичным элементом e² (т.е. квадраты остатков используются как оценки дисперсий). Тогда получается следующая скорректированная оценка ковариацион-

ной матрицы a (оценка Уайта или устойчивая к гетероскедастичности оценка):

(Z^rZ)⁻¹ Z^rS²Z (Z^rZ)⁻¹ .

2. Автокорреляция ошибок 265