Алгебра линейной регрессии

6.1. Линейная регрессия

В этой главе предполагается, что между переменными 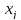, j = 1, . . . , n существует линейная зависимость:

(6.1)

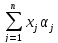j=1

где α_j , j = 1, . . . , n, β (угловые коэффициенты и свободный член) — параметры (коэффициенты) регрессии (их истинные значения), ε — случайная ошибка; или в векторной форме:

xα = β + ε, (6.2)

где x и α — соответственно вектор-строка переменных и вектор-столбец пара- метров регрессии.

Как уже отмечалось в пункте 4.2, регрессия называется линейной, если ее уравнение линейно относительно параметров регрессии, а не переменных. Поэтому предполагается, что x_j , j = 1, . . . , n, могут являться результатом каких-либо функциональных преобразований исходных значений переменных.

Для получения оценок a_j , j = 1, . . . , n, b , e, соответственно, параметров регрессии α_j , j = 1, . . . , n, β и случайных ошибок ε используется N наблюде- ний за переменными x, i = 1, . . . , N , которые образуют матрицу наблюдений X

200 Глава 6. Алгебра линейной регрессии

размерности N × n (столбцы — переменные, строки — наблюдения). Уравнение регрессии по наблюдениям записывается следующим образом:

Xα = 1_N β + ε, (6.3)

где, как и прежде, 1_N — вектор-столбец размерности N , состоящий из еди- ниц, ε — вектор-столбец размерности N случайных ошибок по наблюдениям; или в оценках:

Xa = 1_N b + e. (6.4)

Собственно уравнение регрессии (без случайных ошибок) xα = β или xa = b определяет, соответственно, истинную или расчетную гиперплоскость (линию, плоскость, ... ) регрессии.

Далее применяется метод наименьших квадратов: оценки параметров регрессии находятся так, чтобы минимального значения достигла остаточная дисперсия:

.

.

1 1

_s2

N

_e = _N e^te = _N

a^tX^t − b1^t

(Xa − 1_N b) .

Из равенства нулю производной остаточной дисперсии по свободному члену b

следует, что

x¯a = b (6.5)

и

t

1_N e = 0. (6.6)

Действительно,

∂s² 2

−

1

e ₌ r

∂b N ^N





(Xa − 1_N b) =

− 2 (x¯a − b) ,

2

N

^ − _N 1^r e.

Вторая производная по b равна 2, т.е. в найденной точке достигается минимум.

Здесь и ниже используются следующие правила матричной записи результатов диф- ференцирования линейных и квадратичных форм.

Пусть x, a — вектор-столбцы, α — скаляр, а M — симметричная матрица. То- гда:

^dxα = x, ^∂xra = a, ^∂xrM = M, ^∂xrMx = 2M x.

dα ∂x ∂x ∂x

(См. Приложение A.2.2.)

6.2. Простая регрессия 201

Этот результат означает, что точка средних значений переменных лежит на расчетной гиперплоскости регрессии.

В результате подстановки выражения b из (6.5) через a в (6.4) получается другая форма записи уравнения регрессии:

X^ˆ a = e, (6.7)

где X^ˆ = X − 1_N x¯ — матрица центрированных значений наблюдений.

(6.3, 6.4) — исходная, (6.7) — сокращенная запись уравнения регрессии. Минимизация остаточной дисперсии по a без дополнительных условий приве-

дет к тривиальному результату: a = 0. Чтобы получать нетривиальные решения,

на вектор параметров α и их оценок a необходимо наложить некоторые огра- ничения. В зависимости от формы этих ограничений возникает регрессия разного вида — простая или ортогональная.