4. Оптика квантовых точек

А.В. Федоров, А.В. Баранов

ГОИ им. С.И. Вавилова, Санкт-Петербург

a_v_fedorov@inbox.ru

4.1. Введение

Важнейшим объектом физики низкоразмерных полупроводниковых гетероструктур являются так называемые квазинульмерные системы или квантовые точки. Дать точное определение квантовых точек достаточно трудно. Это связано с тем, что в физической литературе квантовыми точками называют широкий класс квазинульмерных систем, в которых проявляется эффект размерного квантования энергетических спектров электронов, дырок и экситонов. К этому классу, прежде всего, относят полупроводниковые кристаллы, у которых все три пространственных размера порядка боровского радиуса экситона Rex в объемном материале. Данное определение предполагает, что квантовая точка находится в вакууме, газовой или жидкой среде, либо ограничена каким-либо твердотельным материалом, отличающимся от материала, из которого она изготовлена. В этом случае трехмерное пространственное ограничение элементарных возбуждений в квантовых точках обусловлено наличием границ раздела между различными материалами и средами, т. е. существованием гетерограниц. Такие квантовые точки часто называют микроили нанокристаллами. Однако это простое определение не является полным, поскольку есть квантовые точки, для которых гетерограницы в одном либо двух измерениях отсутствуют. Несмотря на это, движение электронов, дырок или экситонов в таких квантовых точках пространственно ограничено из-за наличия потенциальных ям, возникающих, например, благодаря механическим напряжениям или флуктуациям толщины полупроводниковых слоев. В этом смысле можно сказать, что квантовая точка – это любая трехмерная потенциальная яма, заполненная полупроводниковым материалом, с характерными размерами порядка Rex, в которой движение электронов, дырок и экситонов пространственно ограничено в трех измерениях. В настоящее время для изготовления квантовых точек применяют практически любые полупроводниковые соединения, например A1B7, A2B6 и A3B5, а также Ge и Si.

Среди всего многообразия различных квантовых точек можно выделить несколько основных типов, которые наиболее часто используются в экспериментальных исследованиях и приложениях. Прежде всего, это нанокристаллы в жидкостях, стеклах и в матрицах широкозонных диэлектриков (рис. 4.1). Если они выращиваются в стеклянных матрицах, то, как правило, имеют сферическую форму. Именно в такой системе, представлявшей собой квантовые

180 А.В. Федоров, А.В. Баранов

точки из CuCl, внедренные в силикатные стекла, при исследовании однофотонного поглощения был впервые обнаружен эффект трехмерного размерного квантования экситонов [1]. Эта работа положила начало бурному развитию

стекло

R

CdSe

Рис. 4.1. Квантовые точки в стеклянной матрице, представляющие собой сферы с радиусом R.

физики квазинульмерных систем. Квантовые точки в кристаллической диэлектрической матрице могут быть прямоугольными параллелепипедами, как это имеет место для квантовых точек на основе CuCl, встроенных в NaCl. Нанокристаллами являются и квантовые точки, выращенные в полупроводниковых матрицах методом капельной эпитаксии.

Рис. 4.2. Самоорганизованные квантовые точки, выращенные методом Странски– Крастанова. 1 и 4 – буферные слои GaAs, 2 – квантовые точки InAs, 3 – смачивающий слой InAs, 5 – легированная подложка GaAs.

Другим важным типом квантовых точек являются так называемые самоорганизованные квантовые точки, которые изготавливаются методом Странски–Крастанова с помощью техники молекулярно лучевой эпитаксии (рис. 4.2). Их отличительной особенностью является то, что они связаны между собой посредством сверхтонкого смачивающего слоя, материал которого совпадает с материалом квантовых точек. Таким образом, в этих квантовых

точках отсутствует одна из гетерограниц. К этому же типу, в принципе, могут быть отнесены пористые полупроводники, например пористый Si, а также потенциальные ямы в тонких полупроводниковых слоях, возникающие благодаря флуктуациям толщины слоев.

Квантовые точки, индуцированные механическими напряжениями, можно отнести к третьему типу (рис. 4.3). Они образуются в тонких полупроводниковых слоях благодаря механическим напряжениям, которые возникают из-за рассогласования постоянных решетки материалов гетерограниц. Эти механические напряжения приводят к появлению в тонком слое трехмерной потенциальной ямы для электронов, дырок и экситонов. Из рис. 4.3 видно, что

Рис. 4.3. Структура с индуцированными механическими напряжениями InGaAs квантовыми точками. 1 – накрывающий слой GaAs; 2 – самоорганизованные InP квантовые точки, которые задают механические напряжения, приводящие к возникновению трехмерных потенциальных ям в слое InGaAs; 3 и 6 – буферные слои GaAs; 4 – тонкая InGaAs квантовая яма, в которой образуются индуцированные механическими напряжениями квантовые точки; 5 – квантовые точки; 7 – подложка GaAs. Точечными линиями показаны профили механических напряжений.

такие квантовые точки не имеют гетерограниц в двух направлениях. Технология изготовления различных квантовых точек описана в большом

числе научных публикаций, среди которых следует отметить специальные главы в монографиях [2–4].

Как упоминалось выше, характерный линейный размер области пространственного ограничения движения электронов, дырок и экситонов в квантовой точке столь мал, что возникает эффект размерного квантования их энергетических спектров. Однако трехмерное пространственное ограничение приводит не только к размерному квантованию электронной подсистемы твердого тела, но и к квантованию других его подсистем, обладавших в исходном объемном материале непрерывным энергетическим спектром, например колебательной ядерной подсистемы (фононы). Кроме того, пространственное ограничение модифицирует взаимодействие различных квазичастиц квантовой точки друг с другом и с внешними полями. Перестройка энергетического спектра квантовых точек по сравнению с объемными материалами и

182 А.В. Федоров, А.В. Баранов

изменение взаимодействий их элементарных возбуждений, индуцированное пространственным ограничением, проявляется в откликах таких объектов на внешние возмущения. В частности, радикально модифицируются такие оптические отклики квантовых точек, как одно- и многофотонное поглощение, квазиупругое, комбинационное и гиперкомбинационное рассеяние света, а также различные типы люминесценции. Меняются спектральные положения линий, их ширины и относительные амплитуды, а кроме того, существенно изменяются скорости дефазировки оптических переходов и скорости релаксации возбужденных состояний, которыми определяются нестационарные отклики квантовых точек на импульсное оптическое возбуждение.

Неослабевающий интерес к квантовым точкам вызван не только тем, что они обладают уникальными физическими свойствами. Кроме этого, квантовые точки являются чрезвычайно перспективными объектами в смысле практических приложений. На их основе уже создано достаточно большое число различных электронных и оптоэлектронных устройств и приборов, примером которых могут служить лазеры и фотоприемники. Квантовые точки служат рабочим элементом в одноэлектронных транзисторах, используемых для построения процессоров и оперативной памяти компьютеров. Нанокристаллы различных типов применяются даже в биологии и медицине, например в качестве сенсоров и люминесцентных меток. Возможность практического использования квантовых точек в различных областях человеческой деятельность основана, прежде всего, на размерной зависимости их физических свойств. Вследствие этой зависимости, варьируя лишь размеры квантовых точек, можно получать такие их параметры, которые важны для практики. Есть все основания полагать, что со временем прикладное значение квантовых точек будет возрастать.

4.1.1.Состояния размерного квантования электронных и фононных возбуждений квантовых точек

Прежде чем обсуждать оптические свойства полупроводниковых квантовых точек, необходимо подробнее остановиться на эффектах размерного квантования, возникающих в таких системах. Сделаем это на примере достаточно простых физических моделей, в рамках которых удается получить аналитические результаты, качественно описывающие свойства практически любых объектов с трехмерным пространственным ограничением.

Размерное квантование электронной подсистемы квантовых точек

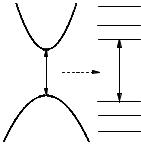
Эффект размерного квантования заключается в том, что при уменьшении линейных размеров объекта квазинепрерывные энергетические спектры и волновые функции его элементарных возбуждений радикально модифицируются. В случае квантовых точек вместо непрерывного спектра возникают дискретные уровни размерного квантования (рис. 4.4). Рассмотрим этот эффект

для случая полупроводниковых квантовых точек простой формы, встроенных в диэлектрическую среду [5].

Рис. 4.4. Схема, иллюстрирующая трансформацию непрерывного энергетического спектра зоны проводимости Ec(k) и валентной зоны Ev(k) объемного полупроводника в дискретный спектр состояний квантовой точки. Eg и EgKT – ширины запрещенной зоны в объемном материале и в квантовой точке.

Для описания энергетического спектра и волновых функций низкоразмерных систем наиболее часто используется та или иная форма метода эффективной массы (kP-теория возмущений) [6], детально разработанного для объемных твердых тел [7]. Привлекательность этого подхода основана на том, что он в ряде случаев позволяет получать аналитические результаты, явно учитывающие граничные условия и форму наноразмерных структурных элементов. Кроме того, в рамках kP-теории возмущений относительно легко учесть взаимодействия электронной подсистемы низкоразмерных систем с колебаниями решетки, статическими деформациями и внешними полями. Удивительным успехом данного подхода является то обстоятельство, что он позволяет объяснить многие качественные закономерности, присущие низкоразмерным системам, даже на основе простейшей двухзонной модели полупроводника, которая явно учитывает лишь одну зону проводимости (c) и одну валентную зону (v).

Основная идея kP-теории возмущений заключается в том, что волновая функция электрона (дырки) представляет собой линейную комбинацию произведений быстро осциллирующих в области элементарной ячейки кристалла блоховских амплитуд un(r) и медленно меняющихся в масштабе элементарной ячейки огибающих волновых функций 'n(r)

n

В (4.1) суммирование ведется по вырожденным состояниям. В случае простой орбитально-невырожденной зоны (например, зоны проводимости в прямозонных полупроводниках A3B5) в (4.1) остается лишь одно слагаемое, используя которое, можно получить с помощью стандартной процедуры [7]

184 А.В. Федоров, А.В. Баранов

уравнение Шредингера для огибающих волновых функций квантовой точки

где m* – эффективная масса носителя заряда в рассматриваемой зоне, а V(r) – трехмерная потенциальная яма, которая пространственно ограничивает движение носителей заряда. Отсюда следует, что для однозонной модели квантовой точки задача на собственные значения сводится к хорошо известной из курса квантовой механики (например, [8]) задаче о движении частицы в потенциальной яме.

Известно, что в ряде случаев уравнение (4.2) может быть решено аналитически. Прежде всего, предположим, что потенциальная яма V(r) обладает бесконечно высокими стенками. Это предположение является вполне оправданным, если квантовая точка находится, например, в стеклянной матрице. Будем считать также, что квантовая точка представляет собой сферу радиуса R (рис. 4.1). Тогда потенциальная яма имеет вид

Благодаря сферической симметрии задачи переменные в (4.2) разделяются. Волновые функции и энергии электрона (дырки) в квантовой точке при условиях '(0) , ∞ и '(r)||r|=R = 0 определяются следующими выражениями:

В (4.4) n, l и m – главное квантовое число, угловой момент и его проекция, соответственно, jl(x) и Ylm( ) – сферические функции Бесселя и сферические гармоники [9], knl = nl=R, nl – n-й корень сферической функции Бесселя l-го порядка ( jl( nl) = 0). Из (4.4) прямо следует, что трехмерное пространственное ограничение движения носителей заряда в квантовой точке приводит к расщеплению их непрерывного энергетического спектра Ec(v)(k) = ~2k2=2mc(v) на дискретные уровни размерного квантования Enl (рис. 4.4). Кроме того, оказывается, что энергия дискретных уровней обратно пропорциональна квадрату радиуса квантовой точки. Аналогичные результаты могут быть получены для квантовых точек в форме прямоугольного параллелепипеда [10]:

где вектором n = (nx; ny; nz) обозначен набор трех квантовых чисел nx, ny и nz, принимающих целые значения; kni = ni=Li для i = x; y; z; Li – длина ребра

параллелепипеда в i-м направлении; kn = (n2x=L2x + n2y =Ly2 + n2z =Lz2)1=2. В случае цилиндра с высотой h и радиусом основания 0 волновые функции и энергии

равны

knl = nl= 0, nl – n-й корень функции Бесселя l-го порядка (Jl( nl) = 0).

До сих пор мы рассматривали одночастичные состояния электронной подсистемы квантовых точек (4.4)–(4.6), однако во многих случаях интерес представляют ее двухчастичные состояния. Это связано с тем, что при межзонных переходах в квантовых точках, как и в объемных полупроводниках, возникают электрон-дырочные пары. Разноименно заряженные частицы, составляющие пару, связаны друг с другом кулоновским взаимодействием, которое меняет ее энергию и может приводить к образованию экситона. Чтобы выяснить пределы применимости одночастичного описания электронной подсистемы квантовой точки, сравним суммарную энергию размерного квантования электрона и дырки Esum = Ecn + Evn с энергией их кулоновского взаимодействия |Vcoul| = e2="0|rc − rv|. Здесь "0 – низкочастотная диэлектрическая проницаемость материала квантовой точки, а rc и rv – координаты электрона и дырки. Очевидно, что кулоновскими поправками к энергии электрон-дырочной пары можно пренебречь при выполнении неравенства Esum >> |Vcoul|. Для сферической квантовой точки с радиусом R при условии, что |rc − rv| ≈ R, это неравенство сводится к

где = mcmv=(mc + mv) – приведенная масса электрона и дырки. Таким образом, одночастичное описание электронного энергетического спектра квантовой точки применимо, если боровский радиус экситона Rex существенно превышает ее радиус R. Про такие квантовые точки говорят, что они находятся в режиме сильного конфайнмента (пространственного ограничения) [11]. Противоположный предельный случай Rex << R принято называть режимом слабого конфайнмента, или экситонным режимом.

Рассмотрим квантовую точку с электроном в зоне проводимости и дыркой в валентной зоне, которые связаны кулоновским взаимодействием. В отличие от (4.2) такая система описывается следующим уравнением Шредингера:

два первых слагаемых в левой части уравнения соответствуют кинетическим энергиям электрона и дырки, V(rc; rv) = V(rc) + V(rv) – сумма трехмерных потенциалов для частиц, образующих электрон-дырочную пару. Отметим, что уравнение Шредингера (4.8) не может быть решено точно даже в простейшем случае сферической потенциальной ямы V(rc(v)) с бесконечно высокими стенками (4.3). Это связано с тем, что мы, по существу, имеем дело с задачей трех тел, в которой роль третьей частицы играет потенциальная яма [12]. Получим приближенное аналитическое решение уравнения (4.8),

186 А.В. Федоров, А.В. Баранов

которое наиболее близко по форме к решению хорошо известной задачи об экситоне Ванье - Мотта в объемном полупроводнике [13]. Для этого в (4.8) перейдем к системе координат, связанной с движением центра масс электрона и дырки и их относительным движением,

где M = mc + mv. В этих координатах уравнение (4.8) имеет вид

причем потенциал квантовой ямы приобретает достаточно сложную форму V(x; X) = V(X + x v) + V(X − x c), где c(v) = mc(v)=M, и не допускает разделения переменных. Таким образом, собственные функции задачи об экситоне в квантовой точке '(x; X), вообще говоря, нельзя представить в виде произведения волновых функций, описывающих движение его центра масс '(X) и относительного движения электрона и дырки '(x). Чтобы обойти эту трудность в режиме слабого конфайнмента (Rex << R) вместо V(x; X) используют “псевдопотенциал”, который выбирают из условий физической разумности и максимальной простоты. Начиная с работы [5] при аналитическом описании экситонного режима вместо V(x; X) часто применяется потенциал V(X), имеющий форму (4.3). Такая аппроксимация уместна, поскольку для положения центра масс естественным, хотя и несколько завышенным, граничным условием является неравенство |X| ≤ R. Очевидно, что указанная замена – достаточно грубое приближение – приводит к существенным потерям при описании экситона в квантовой точке. Действительно, потенциал V(X) учитывает влияние конфайнмента только на трансляционное движение экситона как целого, относительное же движение электрона и дырки остается невозмущенным. Единственным, но очень важным достоинством V(X) является чрезвычайная простота такого потенциала, позволяющая точно решить задачу о движении экситона. В результате для сферической квантовой точки собственные функции и собственные энергии экситона определяются выражениями

где 'n′l′m′ (x) – водородоподобные волновые функции объемного экситона [14]

в состояниях относительного движения, характеризуемых квантовыми числами n′, l′ и m′, Nn′l′ = 2[(n′ − l′ − 1)!=((n′ + l′)!)3]1=2=n′2,

Fn′l′ (x) = xl′ e−x=2Ln2′l′−+l′1−1(x);

Lba(x) – обобщенный полином Лагерра; волновая функция 'nlm(X), описывающая трансляционное движение экситона, совпадает с выражением (4.4), в котором нужно сделать замену r → X; Eg – ширина запрещенной зоны объемного полупроводника; En′ = Ry=n′2 – энергии ионизации уровней неподвижного объемного экситона; Ry = e4=(2"20~2) – экситонный ридберг; энергии размерного квантования трансляционного движения экситона ~2knl2 =2M получаются из (4.4) путем замены m* → M. Из (4.11) видно, что экситонное состояние описывается удвоенным набором квантовых чисел, одна половина которых относится к относительному, а другая – к его трансляционному движению. Другой важной особенностью задачи об экситоне в квантовой точке является то, что энергии размерного квантования определяются суммарной массой электрона и дырки M. Легко показать, что волновые функции и энергии экситона в квантовых точках в форме прямоугольного параллелепипеда и цилиндра могут быть получены из (4.11), если для волновых функций трансляционного движения и энергий размерного квантования использовать выражения (4.5) и (4.6), в которых должна быть проведена замена m* → M.

Следует заметить, рассмотренный подход, основанный на аппроксимации V(x; X) ≈ V(X), имеет физический смысл, если волновые функции 'n′l′m′ (x) exp(−x=n′Rex) локализованы в области n′Rex R*, где R* – характерный размер квантовой точки. Это существенно ограничивает применимость такого подхода, в частности, при описании многоквантовых процессов, когда необходим учет большого числа промежуточных состояний. С другой стороны, используя иную аппроксимацию V(x; X) ≈ V(X) + V(x) [15], можно получить аналитические выражения для собственных функций и состояний экситона, которые имеют более широкую область применимости и учитывают влияние конфайнмента на относительное движение электрона и дырки (V(x)). Основная сложность, возникающая в этом случае, состоит в выборе потенциала V(x), для которого трудно задать даже граничную поверхность. Действительно, для расстояния между электроном и дыркой (например, в сферической квантовой точке) можно указать лишь область, в которой должна находиться граница R ≤ |x| ≤ 2R. Нижний предел этого двойного неравенства соответствует случаю, когда одна из частиц экситона находится в центре квантовой точки, а верхний предел достигается, если электрон и дырка расположены на противоположных концах диаметра квантовой точки. Если предположить, что для относительного движения потенциальная яма имеет форму (4.3), и учесть с помощью подгоночного параметра неопределенность положения ее границы, то полный “псевдопотенциал” будет иметь вид

Задача на собственные значения для экситона в этом псевдопотенциале решается точно. Волновые функции, как и прежде, определяются выражением (4.11), причем 'nlm(X) совпадают с волновыми функциями трансляционного движения в псевдопотенциале V (X), а радиальная часть 'n′l′m′ (x) теперь дается выражением

188 А.В. Федоров, А.В. Баранов

где M [an′l′ + l′ + 1; 2l′ + 2; cn′l′ x=R] – регулярная в нуле функция Куммера, An′l′

– нормировочная постоянная. Граничное условие Fn′l′ ( R) = 0 является, по существу, уравнением на собственные значения. Необходимо раздельно рассмотреть области отрицательных и положительных собственных значений. В первом случае энергия относительного движения электрона и дырки равна

Ry

En′l′ = Ry · n′l′ (d) = −Nn2′l′ (d) ;

при этом d = R=Rex – относительный радиус квантовой точки, an′l′ = −Nn′l′ (d),

En′l′ = Ry · n′l′ (d) = Ry · kn2′l′ (d);

где kn′l′ (d) – соответствующий корень уравнения

{ [ ] }

Re exp (−id kn′l′ (d)) M i + l′ + 1; 2l′ + 2; i2d kn′l′ (d) = 0; kn′l′ (d)

т.е. an′l′ = i=kn′l′ (d), cn′l′ = i2dkn′l′ (d). Таким образом, полную энергию экситона в псевдопотенциале (4.13) можно представить как

следовательно, формально мы получили весь энергетический спектр как при положительных, так и при отрицательных значениях n′l′ (d). Перечислим его основные особенности, связанные с влиянием конфайнмента на относительное движение электрона и дырки. Во-первых, при каждом фиксированном d число уровней с отрицательной величиной n′l′ (d) конечно, причем последовательно уменьшается с уменьшением d и существует такое критическое значение dc, при котором уровни данного типа исчезают полностью. Характер этого исчезновения таков, что с уменьшением d отрицательные энергии стремятся к нулю, а затем меняют знак, т.е. имеет место индуцированный конфайнментом эффект выталкивания уровней из кулоновской потенциальной ямы. Во-вторых, конфайнмент снимает вырождение по орбитальному моменту относительного движения l′, которое присуще чисто кулоновской задаче.

Приведенные выше результаты содержат важные качественные особенности, характерные для квантовых точек. Видно, что энергетический спектр зависит как от их размеров, так и от их формы. Кроме того, геометрическая

симметрия квантовых точек, проявляющаяся в явном виде огибающих волновых функций электронных (экситонных) состояний, определяет правила отбора при различных квантовых переходах между этими состояниями. В то же время ясно, что собственные функции и собственные энергии, полученные в рамках столь радикальных приближений, не могут быть универсальными и не описывают свойства многих реальных низкоразмерных систем. Действительно, одним из чрезвычайно сильных предположений, позволившим найти аналитические выражения для энергетических спектров электронной подсистемы квантовых точек, является утверждение о бесконечной глубине потенциальных ям для электронов, дырок и экситонов. Отсюда немедленно следует, что в качестве граничных условий может использоваться требование равенства нулю огибающих волновых функций на границе раздела материалов. Однако, как уже отмечалось, модель с бесконечными потенциальными ямами может быть более или менее адекватна для изолированных наноструктур, находящихся в вакууме или газовой среде, а также для квантовых точек, выращенных в стеклах или широкозонных диэлектриках. Если же квантовые точки встроены в полупроводниковые матрицы, то необходимо учитывать конечную глубину потенциальных ям, причем она будет различной для электронов и дырок. При этом возникают две проблемы. Первая из них связана с тем, что на границе раздела сред должна быть непрерывной полная волновая функция, которая является произведением блоховской амплитуды и медленной огибающей, а также нормальная к границе раздела составляющая градиента полной волновой функции. Однако в методе эффективной массы блоховские амплитуды явно не определены и входят в теорию только через различные матричные элементы. Другая проблема связана с тем, что границы квантовых точек являются резкими, т.е. соответствующий им потенциал существенно меняется на расстоянии порядка постоянной решетки. Быстрое изменение потенциала может приводить к значительному перемешиванию состояний рассматриваемой зоны и состояний, принадлежащих другим зонам. Этот эффект не может быть удовлетворительно описан в рамках метода эффективной массы, который применим лишь к медленно меняющимся потенциалам [6, 7]. Строгий учет конечной глубины потенциальных ям и резкой границы раздела сред возможен лишь в результате сложных численных расчетов. Тем не менее, в настоящее время, общепринятым является использование метода эффективной массы с граничными условиями, сформулирован-

ными для огибающих волновых функций 'A, 'B и эффективных масс mA, mB в материалах A и B: mA'A = mB'B, m−A(1+ )@'A=@z = m−B(1+ )@'B=@z. Численные расчеты (см., например, [16, 17]) показали, что величина лежит в

области от −1=2 до 0. Так, например, для сферической квантовой точки в режиме сильного конфайнмента использование приведенных выше граничных условий дает следующий результат [18] для волновых функций электронов в конечной потенциальной яме с глубиной V:

190 А.В. Федоров, А.В. Баранов

{

×kl(x2) jl(x1r=R); r ≤ R; jl(x1)kl(x2r=R); r > R;

где

√ √

x1 = R 2m1Enl=~2; x2 = R 2m2(V − Enl)=~2;

kl – модифицированная сферическая функция Бесселя, m1 и m2 – эффективные массы электрона внутри и вне квантовой точки. Энергии электронных состояний Enl определяются секулярным уравнением

m2 x1kl(x2) j′l (x1) = m1 x2kl′(x2) jl(x1):

Дальнейшее уточнение энергетического спектра электронной подсистемы квантовых точек связано с отказом от двухзонной модели полупроводника. Действительно в полупроводниковых материалах с симметрией Oh и Td валентная зона обладает сложной структурой, т. е. состоит из подзон тяжелых, легких и спин-орбитально отщепленных дырок. Учет этого важного обстоятельства возможен при использовании многозонных моделей, основанных на kP-теории возмущений [6, 7]. В простейшем варианте такой модели подзоны валентной зоны считаются независимыми друг от друга. При этом энергетический спектр электронных и экситонных состояний квантовых точек будет суперпозицией спектров изолированных зон. Единственным, но крайне важным достоинством такой модели является возможность получения простых аналитических результатов, необходимых для качественной оценки влияния конфайнмента на свойства низкоразмерных систем. Более адекватное описание зонного спектра электронной подсистемы квантовых точек, путем последовательного учета kP-возмущений, смешивающих различные зоны или подзоны валентной зоны, требует громоздких численных расчетов собственных энергий и собственных функций. Анализ различных аспектов этой проблемы и результаты вычислений, относящиеся к квантовым точкам, приведены, например, в работах [19–24].

Кроме обсуждавшихся выше режимов сильного и слабого конфайнмента, несомненный интерес представляет промежуточный случай, когда характерный размер наноструктуры равен по порядку величины Rex. В этом режиме промежуточного конфайнмента при определении энергетического спектра квантовых точек необходим учет экситонных эффектов, причем пространственное ограничение оказывает существенное влияние как на трансляционное, так и на относительное движение экситона. Очевидно, что задача на собственные значения и собственные функции в режиме промежуточного конфайнмента может быть решена лишь численными методами даже в рамках двухзонной модели полупроводника и в предположении о бесконечно высоких потенциальных барьерах [12, 25].

Энергетический спектр и волновые функции электронной подсистемы квантовых точек рассчитывались и другими методами. Так, например, в работах [26, 27] для этого использовались модели, основанные на приближении

сильной связи, а в [28, 29] различные модификации модели псевдопотенциала. Достаточно подробное изложение различных подходов к данной проблеме с большим количеством ссылок на оригинальные работы можно найти в обзорах [11, 30]. Там же обсуждаются различные аспекты тонкой структуры энергетического спектра электронов, дырок и экситонов в квантовых точках, связанной со спин-орбитальным и обменным взаимодействиями. Кроме того, в [30] приведены результаты исследования самоорганизованных квантовых точек различной формы, выращенных в разнообразных полупроводниковых матрицах. Эти данные существенно дополняют монографию [3].

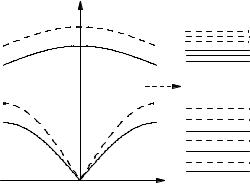
Размерное квантование колебательной подсистемы квантовых точек

Ясно, что трехмерное пространственное ограничение модифицирует не только электронные состояния квантовой точки, но и колебания ее решетки, т. е. акустические и оптические фононы (рис. 4.5). Рассмотрим эту проблему на

ωTAnl

k

Рис. 4.5. Схема, иллюстрирующая трансформацию непрерывного энергетического спектра продольных и поперечных акустических и оптических фононов объемного полупроводника со структурой цинковой обманки в дискретный спектр колебательных состояний сферической квантовой точки.

примере изолированного нанокристалла, полагая, что он обладает свободной либо жестко закрепленной границей. В этом случае решеточные колебания квантовой точки не взаимодействуют с окружающей ее средой. Для описания фононного спектра нанокристалла мы воспользуемся моделью изотропного упругого континуума, в рамках которой удается получить ряд полезных аналитических результатов, качественно характеризующих и более реалистические с физической точки зрения системы.

Рассмотрение начнем с акустических фононов, представляющих собой звуковые волны. Амплитуды колебаний u изотропного упругого континуума описываются следующим хорошо известным векторным уравнением [31]:

плотность массы, а и – упругие постоянные материала. Предположим, что изолированная квантовая точка имеет сферическую форму. Если поверхность S нанокристалла свободна, то нормальная компонента тензора механических напряжений ˆ на границе обращается в нуль

В обоих случаях собственными функциями уравнения (4.15) являются чисто поперечные колебательные моды частоты !, которые часто называют торсионными,

и смешанные продольно-поперечные колебательные (сфероидальные) моды

где R – радиус квантовой точки, kT = !=vT , kL = !=vL, коэффициенты plm, qlm и rlm определяются граничными условиями и условием нормировки; Llm, Mlm, Nlm – векторные сферические гармоники, которые выражаются через функции lm(kr) = jl(kr)Ylm( ),

Nlm(kr) = 1 rotMlm(kr):

k

Легко показать, что угловым моментом l = 0 могут обладать только сфероидальные моды, которые в этом случае становятся чисто продольными. Оба граничных условия (4.16) и (4.17) приводят к размерному квантованию энергетического спектра акустических фононов (рис. 4.5). Для торсионных колебаний (4.18) уравнение на собственные значения в случае свободной поверхности квантовой точки (4.16) имеет вид

а в случае жестко закрепленной поверхности (4.17) частоты размерно квантованных акустических фононов

194 А.В. Федоров, А.В. Баранов

Однако, в отличие от задачи об акустических фононах, величины u теперь имеют смысл смещения положительного иона относительно отрицательного иона. Поскольку в ионных материалах продольные оптические колебания решетки приводят к появлению электрического поля E = −grad 'op, то для решения задачи об оптических фононах необходимо использовать уравнения Максвелла. Мы в дальнейшем будем пренебрегать запаздыванием электромагнитных полей и, следовательно, можем ограничиться одним из этих уравнений для вектора электрической индукции D, зависящего от E и u,

которое дополняет феноменологическое уравнение для u

где !T O – частота поперечного оптического фонона в объемном материале в центре зоны Бриллюэна при k = 0 (рис. 4.5), L и T – параметры, характеризующие кривизну дисперсионных ветвей оптических фононов в объемном

√

материале, = !T O ("0 − "∞) =4 , "0 и "∞ – низко и высокочастотные диэлектрические проницаемости полупроводника, – плотность приведенной массы положительных и отрицательных ионов. В (4.28) знаки слагаемых, содержащих L и T , выбраны в соответствии с рис. 4.5, т.е. так, чтобы с увеличением волнового вектора k частоты объемных фононов уменьшались. Чтобы система (4.27) и (4.28) была замкнутой, необходимо задать зависимость D от E и u. Мы будем использовать хорошо известное в теории полупроводников [13] соотношение

Общее решение уравнений (4.27), (4.28) и (4.29) может быть получено методом, изложенным в работе [32], однако оно достаточно громоздко [33] и его детальный анализ выходит за рамки нашей работы. В то же время необходимо упомянуть ряд важных выводов, основанных на таком анализе. Во-первых, как и в случае акустических фононов, для оптических фононов имеет место эффект размерного квантования. Так, например, в случае квантовых точек с жестко закрепленной поверхностью частоты чисто поперечных оптических колебаний имеют вид

а для чисто продольных колебаний (l = 0)

в объемном материале в центре зоны Бриллюэна. Во-вторых, собственными функциями рассматриваемой задачи являются чисто поперечные моды

uT O(r), определяемые выражением (4.18), в котором нужно сделать замену

√

kT → kT O = !2T O − !2= T , а также смешанные моды

где последнее слагаемое описывает вклад поверхностных оптических коле-

√

баний, kLO = !2LO − !2= L. Из (4.32) следует, что угловым моментом l = 0

могут обладать только смешанные моды, которые в этом случае становятся чисто продольными. Коэффициенты plm, qlm, rlm, slm и энергетический спектр смешанных мод определяются граничными условиями (4.16) или (4.17) и условием нормировки, к которым нужно добавить требование непрерывности на границе электрического потенциала ' и нормальной компоненты вектора электрической индукции D.

Необходимо иметь в виду, что модель изолированной квантовой точки может применяться лишь к ограниченному числу реальных систем. Действительно изолированным являются нанокристаллы в вакууме, которые имеют свободную поверхность. Менее обосновано использование такой модели для описания квантовых точек в газовых и жидких средах. Если же нанокристаллы находятся в твердотельной матрице, то представление об изолированной квантовой точке, по крайней мере в отношении акустических колебаний, теряет смысл [34]. Контакт нанокристалла с диэлектрической или полупроводниковой матрицей приводит к тому, что акустические фононы материалов с квантовыми точками являются единой подсистемой для точек и матрицы. Эффект размерного квантования для таких акустических волн отсутствует. В этом случае условия (4.16) и (4.17) должны быть заменены на

играничными условиями на поверхности образца. Здесь S + и S − – граничные поверхности внутри и вне квантовой точки. Таким образом, получается типичная задача рассеяния с непрерывным энергетическим спектром и с собственными состояниями акустических фононов, которые являются хорошо известными стационарными состояниями рассеяния [34].

Для описания оптических колебаний модель изолированной квантовой точки имеет более широкую область применимости, чем для описания акустических фононов. Это связано с тем, что не все твердотельные материалы, используемые в качестве матриц, обладают оптическими колебаниями решетки. К ним в первую очередь относятся разнообразные стекла и кристаллы с одним атомом в элементарной ячейке. Кроме того, если законы дисперсии оптических фононов в материалах, из которых изготовлены нанокристаллы

иматрица, не перекрываются, то модель изолированной квантовой точки может быть использована при описании оптических колебаний нанокристалла.