Лекция 6. Метод разделения переменных исследования устойчивости разностных схем

Этот метод применяется для строгого обоснования устойчивости многих линейных схем и нестрогого, но плодотворного исследования большинства нелинейных задач, возникающих в практике вычислений. При его помощи устанавливается устойчивость в

Рассмотрим применение метода к линейным двуслойным схемам, записанным в канонической форме

(29.4)

где В и А – некоторые разностные операторы, действующие на у (или ) как на функцию пространственной переменной. Например, для явной схемы для уравнения теплопроводности имеем

При фиксированной правой части погрешность решения удовлетворяет однородному уравнению

. (29.5)

Будем искать для этого уравнения частное решение с разделяющимися переменными

. (29.6)

При этом так что- есть множитель ростаq-й гармоники при переходе со слоя на слой. Подставляя (29.6) в (29.5), получим уравнение для определения . (29.7)

Будем считать, что схема (29.4) имеет постоянные коэффициенты и задана на равномерной сетке. Тогда уравнение (29.7) после сокращения множителя exp(iqx) не будет зависеть от координаты х (или от ее индекса n). Следовательно величина не будет зависеть отх или t.

Признак устойчивости. Схема (29.4) с постоянными коэффициентами устойчива по начальным данным, если для всех q выполняется неравенство

(29.8)

Доказательство. Система функций полна и ортогональна на равномерной сеткеРазложим произвольную ошибку начальных данных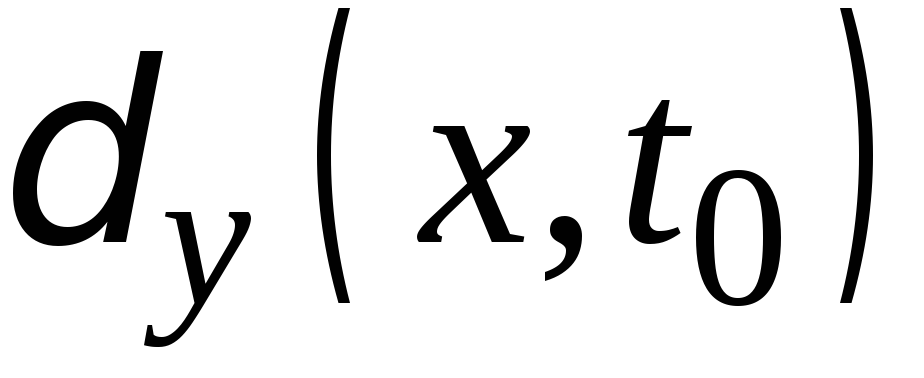в ряд Фурье по этой системе

=.

Поскольку для линейного уравнения (29.4) справедлив принцип суперпозиции, то метод разделения переменных дает для ошибки на слое t_m следующее выражение

=.

Используя ортогональность гармоник, получаем отсюда

При помощи условия (это условие теоремы) преобразуем это неравенство к виду

что совпадает с признаком устойчивости по начальным данным

Утверждение доказано.

Замечание 1. Из признака устойчивости (29.8) и условия ^æ/следует устойчивость схемы по правой части в

Замечание 2. Фактически константа с в (29.8) не должна быть большой, иначе устойчивость будет слабой. Поэтому при проверке этого признака обычно полагают с = 0.

Признак неустойчивости. Если хотя бы для одного q величину нельзя мажорировать величиной, то схема (29.4) неустойчива.

Доказательство. Пусть в начальных данных имеется ошибка вида с даннымq. Тогда к моменту она возрастет враз, что по модулю больше величиныпри сколь угодно большомс. Неограниченный рост ошибки означает неустойчивость схемы.

Пример. Исследуем устойчивость явной схемы

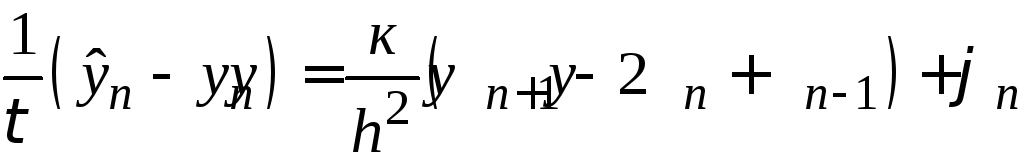
для уравнения теплопроводности. Для этой схемы уравнение

(29.7) примет вид

Отсюда вытекает, что множитель роста

Тогда уравнение с учетом замечания 2 (т.е. условияс = 0) приобретает вид Это неравенство выполняется для любогоq, если

то есть или.

Таким образом, явная схема устойчива условно.

Сходимость разностных схем

Основная теорема. В этом пункте мы рассмотрим задачу для дифференциальных уравнений с граничными условиями

которая на сетке, состоящей из множества регулярных узлов и множества нерегулярных узловаппроксимирована разностной схемой

(30.10)

В конечном итоге нас будет интересовать близость разностного решения у(х) к точному решению u(x), поскольку у(х) определено только на сетке +то сравнивать эти решения надо в сеточной норме.

Определение. Разностное решение у(х) сходится к решению u(x) задачи (30.9), если при(30.11)

разностное решение имеет порядок р, если при

(30.12)

Анализируя сходимость схемы ломаных для обыкновенного дифференциального уравнения, мы видели, что погрешность решения вызвана погрешностью начальных данных и погрешностью аппроксимации, усиливающимися (или ослабляющимися) в ходе расчета. Интуитивно ясно, что для хорошей точности расчета достаточно, чтобы эти погрешности были малы и в ходе расчета не сильно возрастали.

Определение. Разностная схема (30.10) корректна, если ее решение существует и единственно при любых входных данных и, принадлежащих заданным классам функций, и схема устойчива.

Теорема. Если решение дифференциальной задачи существует, разностная схема (30.10) корректна и аппроксимирует дифференциальную задачу (30.9) на данном решении, то разностное решение сходится к точному.

Доказательство. Напишем цепочку преобразований

где есть, по определению, невязка разностной схемы. Делая аналогичное преобразование для краевых условий, получим

(30.13)

Равенства (30.13) представляют собой схему (30.10) с правыми частями, измененными на величину невязки. Поскольку разностная схема устойчива, то для любого найдется такоечтоесли

В силу аппроксимации для любого найдется такоечтопри.

Следовательно, для любого > 0 найдется такоечтопри.

Сходимость доказана.

(Эту теорему кратко формулируют так: «Из аппроксимации и устойчивости следует сходимость»).

Замечание 1. Некоторые начальные или граничные условия аппроксимируются точно; примером являются граничные условия первого рода если узелх_N сетки расположен на границе х = а. Устойчивости по таким условиям можно не требовать, ибо никакой ошибки в расчет они не вносят (кроме ошибки округления).

Устойчивость по правой части требуется почти во всех случаях, поскольку погрешность аппроксимации в (30.13) эквивалентна некоторой погрешности правой части.

Замечание 2. Аппроксимацию часто проверяют не на решениях дифференциальной задачи (30.9), а на некотором широком классе функций, которому принадлежит решение (обычно на классе функций, непрерывных и ограниченных вместе с некоторым числом своих производных).

Ясно, что если на всех функциях этого класса имеется аппроксимация порядка р, то аппроксимация на решении имеет порядок не ниже р. Так вот из этого замечания следует, что такая аппроксимация достаточна для доказательства теоремы о сходимости.

Замечание 3. При исследовании аппроксимации и устойчивости конкретных разностных схем нередко используют разные нормы для одной и той же функции. Например, при установлении локальной аппроксимации для берется, а при спектральном исследовании устойчивости -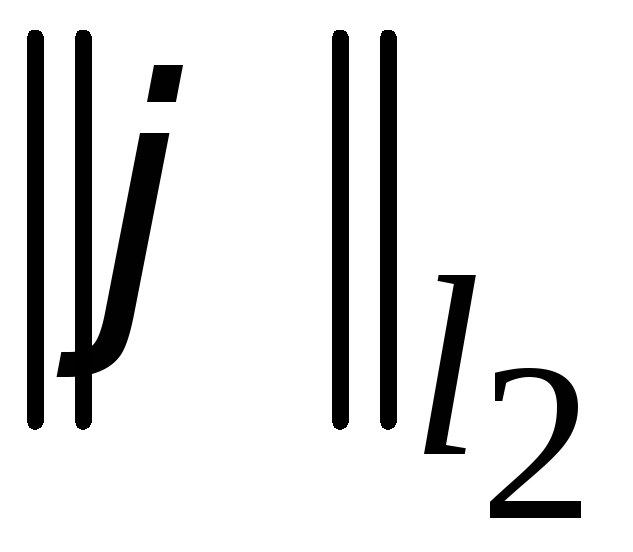. Доказательство сходимости в этом случае справедливо, только если аппроксимация установлена в нормахболее сильных (или тех же самых), чем нормы, использованные для правых частей в определении устойчивости.

Замечание 4. Если аппроксимация или устойчивость условные, то сходимость имеет место при выполнении условий устойчивости и аппроксимации (т.е. при определенных соотношениях между шагами по разным переменным).

Замечание 5. Устойчивость является, как не трудно убедиться, необходимым условием сходимости. В самом деле, если схема неустойчива, то найдутся такие сколь угодно малые ошибки входных данных, которым соответствует значительная погрешность решения. Сходимости при этом быть не может.