Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4612 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Владимирский государственный университет им. Столетовых
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Колебания, волны, оптика

.pdf
Скачиваний:
101
Добавлен:
22.03.2015
Размер:
1.01 Mб
Скачать
☆

Обозначим

qm

= Um (амплитуда напряжения), тогда

 

 

 

 

 

 

C

 

 

 

 

 

 

 

 

 

 

 

UC = Um cos(ω0t + α )

 

 

 

(4)

Сила тока в контуре I = dq

 

 

 

 

.

 

 

 

 

Дифференцируя (3), получим

 

 

 

 

 

dt

 

 

 

 

 

 

 

 

или

 

 

I = -ω0qmsin(ω0t + α)= -Imsin(ω0t + α),

 

 

 

 

 

 

ω0t + α +

π

 

(5)

 

 

 

 

 

 

 

 

 

 

 

 

 

I = Im cos

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

где

Im = ω0qm

 

 

 

 

 

 

 

- амплитуда силы тока в контуре.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Из сравнения выражений (5) и (4) следует, что ток в контуре опережает напряжение на конденсаторе по фазе на π/2.

2. Дифференциальное уравнение затухающих электромагнитных колебаний и его решение. Частота и коэффициент затухания электромагнитных колебаний. Логарифмический декремент затухания и добротность колебательного контура. Рассмотрим колебательный кон-

тур с активным сопротивлением (рис. 29.2).

Второй закон Кирхгофа с учетом напряжения на активном сопротивлении

 

 

R

UC + U R = εs .

 

 

 

 

 

Подставляя UC =

q

dI

 

 

 

 

 

 

 

 

 

 

 

, U R

= IR , εs = − L dt

,

 

 

 

 

 

 

 

 

C

С

L получим

 

 

 

 

 

 

 

q

+ IR = −L dI .

 

 

 

 

 

 

 

 

 

Рис. 29.2

 

C

dt

 

 

Разделив левую и правую части на L и перенося

член из правой части в левую, получим:

dIdt + RL I + LC1 q = 0 .

Обозначая LC1 = ω02 , RL = 2β , где β = 2RL - коэффициент затухания, а

также учитывая, что I = dqdt , уравнение запишется в виде

d 2q + 2β dq + ω20q = 0 dt2 dt

31

Этодифференциальноеуравнениезатухающихэлектромагнитныхколебаний.

При условии β2 < ω02 (т.е. 4RL22 < LC1 ) решение имеет вид

 

 

 

 

 

q = q e−βt cos(ωt + α )

(6)

 

 

 

 

 

 

 

m

 

 

 

 

 

 

 

 

0

 

 

2

 

2

 

1

 

R 2

 

 

где ω = ω

0 − β

 

=

 

−

 

 

- частота затухающих электромагнитных

 

LC

2L

 

 

 

 

 

 

 

 

колебаний; q e−βt

-амплитуда затухающих колебаний; α - начальная фаза.

m

 

 

 

 

 

 

0

 

 

 

 

 

 

Поделив (6) на С, получим выражение напряжения на конденсаторе

 

 

 

U = U

m0

e−βt cos(ωt + α )

 

(7)

 

 

 

 

 

 

 

 

 

 

 

 

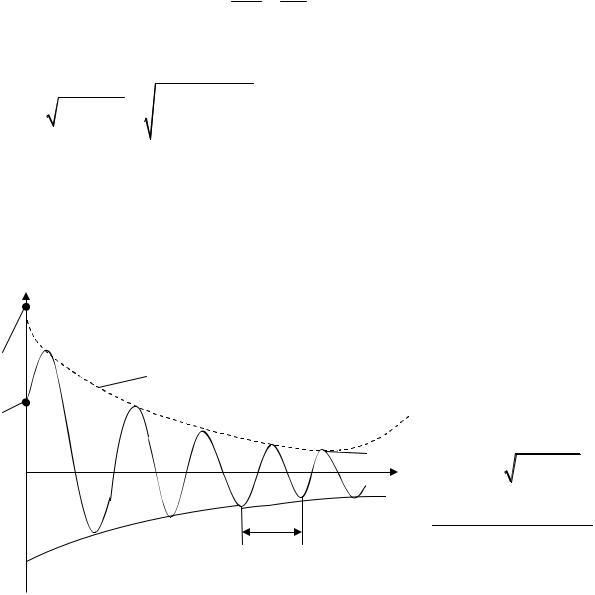
График, соответствующий функции (7), показан на рис. 29.3.

U

 

 

 

U m

 

e -βt -

амплиту-

 

 

 

0

 

 

 

 

 

 

 

 

да затухающих ко-

Um0

Um e−βt

 

 

лебаний

напряже-

 

 

ния; Т - период за-

 

0

 

 

тухающих

колеба-

U0

 

 

 

 

 

 

ний

 

2π =

 

2π

 

 

 

 

 

T =

 

 

.

 

 

 

 

 

 

ω02 − β2

 

 

 

t

 

ω

 

 

 

 

 

Логарифмический

 

 

T

 

декремент

затуха-

 

 

 

ния

 

определяется

 

 

 

 

 

 

Рис. 29.3

 

 

как

 

натуральный

 

 

 

логарифм

отноше-

 

 

 

 

 

 

 

 

ния двух значений

 

 

 

 

амплитуд,

взятых

 

 

 

 

через период.

 

 

U (t )

 

Um0 e

−βt

 

R 2π

 

πR

 

 

λ = ln

= ln

 

= βT =

=

.

(8)

 

 

 

 

 

 

U (t + T )

 

 

2L ω

 

 

 

Um0 e

−β(t+T )

 

 

Lω

 

 

 

 

 

 

 

 

 

 

 

 

 

Добротность Q колебательного контура пропорциональна числу коле-

баний, за которое амплитуда уменьшается в е раз и по определениюQ = λπ .

32

Подставляя в это выражение значение λ , получили

 

πLω

 

Lω

Q =

 

=

 

.

πR

 

 

 

R

Из приведенных формул для λ и Q видно, что затухание пропорцио-

нально R и обратно пропорционально L и ω .

Нетрудно показать, что коэффициент затухания обратен времени τ , за которое амплитуда колебаний уменьшается в е раз, β = 1τ . Это время назы-

вается временем релаксации.

3. Дифференциальное уравнение вынужденных электромагнитных колебаний и его решение. Амплитуда и фаза электромагнитных колебаний. Резонанс в колебательном контуре. Разорвем контур на рис. 29.2

и на образовавшиеся контакты включим источник переменного гармони-

ческого напряжения U = Um cos ωt (рис. 29. 4).

 

 

 

 

 

 

R

 

Включение такого напряжения эквива-

 

 

 

 

 

лентно включению в контур гармонической

 

 

 

 

 

 

 

ЭДС. Второй закон Кирхгофа запишется в

 

 

 

 

 

 

 

 

 

 

 

 

 

 

виде (см. п. 2)

 

 

С

 

 

 

L

IR +

q

= −L dI + Um cos ωt.

(8)

 

 

 

 

 

 

 

 

C

 

 

 

 

U

 

 

dt

 

 

 

 

 

 

Проделав преобразования, аналогич-

 

 

 

 

 

 

 

ные преобразованиям п. 2, получим диф-

 

 

 

 

 

 

 

 

 

 

Рис. 29.4

 

ференциальное уравнение вынужденных

электромагнитных колебаний (для заряда q)

d 2q + 2β dq + ω 2q =

Um

cos ωt

 

dt2

dt

0

L

 

Частное решение этого уравнения имеет вид

q = qm cos(ωt − ψ )

(9)

где qm - амплитуда заряда на конденсаторе; ψ - разность фаз между коле-

баниями заряда и внешним напряжением U.

Продифференцируем (9), получим выражение для тока в контуре

I = −ωq

sin (ωt − ψ ) = I

m

cos

 

ωt − ψ +

π

, где I

m

= ωq ,

m

 

 

 

 

 

 

 

m

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

итак

 

 

I = Im cos(ωt − ϕ)

 

 

 

33

где

ϕ = ψ −

π

сдвиг по фазе между токоми приложенным напряжением.

 

 

2

 

 

 

 

 

 

 

Тангенс угла сдвига (без вывода, см. далее в п. 4 рис. 29.7).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ωL −

1

 

 

 

 

 

 

 

tgϕ =

ωC

 

 

 

 

 

 

 

 

 

 

 

R

 

 

 

 

 

 

 

 

 

 

 

 

 

Из этой формулы следует, что ток отстает по фазе от напряжения, когда

ωL >

1

 

(индуктивный характер нагрузки),( ϕ > 0 ),

и опережает напря-

ωC

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

жение ( ϕ

< 0 ) при ωL <

 

(емкостной характер нагрузки).

ωC

Амплитуда силы

 

 

вывода)

 

 

 

 

 

 

тока (без

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Im = ωqm =

 

 

 

Um

 

 

 

 

(10)

 

 

 

 

 

R

2

 

ωL −

1

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

+

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ωC

 

 

 

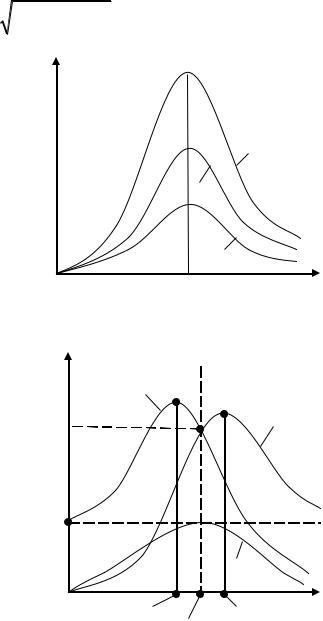
Резонанс в колебательном контуре. Зависимость Im (ω) приводит к тому, что при некоторой частоте значение Im достигает максимума (резонанс). Из формулы (10) следует, что максимум Im будет при минимальном

значении знаменателя, т.е. при ωL − ω1C = 0 . Следовательно резонансная

частота для силы тока совпадает с собственной частотой контураω0 . Резонансные кривые Im (ω) показаны на рис. 29.5. При ω = 0 Im = 0 (при по-

стоянном напряжении установившийся ток в цепи с конденсатором течь не может). Максимум при резонансе оказывается тем выше и острее, чем мень-

ше коэффициент затухания β = 2RL . Заметим, что резонансные частоты для амплитуд напряжений* на отдельных элементах колебательного контура

U R

, UC

и U L

отличаются друг от друга и соответственно равны (без

m

m

m

 

 

 

 

вывода, вывод см. [8])

 

ωR

= ω0 ,

 

 

 

 

 

 

 

 

 

 

 

 

рез

 

 

 

 

ωC

рез

= ω0 1− 2(β / ω0 )2

,

 

 

 

 

 

 

 

* В сокращенном варианте эту часть п. 3 можно пропустить.

34

ωLрез =

Чем меньше β , тем ближе резонансные частоты к ω0 .

Распределение амплитуд напряжений U Rm , UCm и U Lm в

зависимости от частоты ω показано на рис. 29.6.

Явление резонанса в случае электромагнитных колебаний – это возбуждение сильных колебаний при частоте внешнего напряжения, равной или близкой к собственной частоте колебательного контура.

Резонанс используют для выделения из сложного напряжения нужной составляющей.

Чтобы радиоприемник настроить на интересующую нас радиостанцию, необходимо изменением С и L добиться совпадения его собственной частоты с частотой электромагнитных волн, излучаемых радиостанцией.

С явлением резонанса связана и определенная опасность: внешнее напряжение может быть мало, однако напряжения на емкости или индуктивности могут достигать опасного для жизни значения.

ω0

 

.

 

1− 2(β / ω0 )2

 

Im

 

 

β1 < β2 < β3

 

 

 

 

 

 

β1

 

 

β2

 

 

 

β3

 

 

 

ω0

ω

U

 

Рис. 29.5

 

UC

 

 

 

 

 

m

 

QUm

 

 

U L

 

 

m

Um

 

UR

 

m

ωCрез ω

ω

ωLpeз

0

 

Рис. 29.6

4. Переменный ток. Вынужденные электромагнитные колебания можно рассматривать как протекание в цепи, содержащей резистор, индуктивность и емкость переменного тока.

Переменный ток можно считать квазистационарным, т.е. для него мгновенные значения силы тока во всех сечениях цепи практически одинаковы, так как электромагнитное возмущение распространяется по цепи со скоростью, равной скорости света. Для мгновенных значений квазистацианарных токов выполняются уравнения Кирхгофа и Ома.

35

= Um cosωt
= Um cosωt,

Выражение для амплитуды силы тока Im (ω) (10) формально можно

толковать как закон Ома для амплитудных значений тока и напряжения. Стоящую в знаменателе величину обозначают буквой z

z =

R

2

 

ωL −

1 2

 

+

 

 

 

 

 

 

 

 

 

ωC

и называют полным сопротивлением, или импедансом. Величину, стоящую в круглых скобках, обозначают х

 

x = ωL −

1

 

 

 

 

 

 

 

 

ωC

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

xL = ωL

называют

 

 

 

 

 

 

 

 

и называют реактивным сопротивлением. Величину

 

 

 

 

 

 

 

 

 

 

индуктивнымсопротивлением, авеличину

 

x =

 

1

 

 

- емкостнымсопро-

 

 

ωC

 

 

C

 

 

 

 

 

 

 

 

 

 

 

 

 

тивлением, R – активным сопротивлением. Отметим, что индуктивное сопротивление растет с увеличением частоты, а емкостное – уменьшается. Между активным и реактивным сопротивлениями имеется принципиальное различие. Только в активном сопротивлении электромагнитная энергия преобразуется в джоулеву теплоту.

Вернемся к уравнению (8) для колебательного контура, включающего R, L, C и источник переменного гармонического напряжения (см. рис. 29.4). Это уравнение можно записать в виде

L dIdt + RI + Cq

или

UL + UR + UC

где слева записана сумма напряжений на индуктивности U L = L dIdt , актив-

ном сопротивлении UR = RI и емкости UC = Cq . Учитывая соотношения

I = I

m

cos(ωt − ϕ),

I

m

= ωq , ϕ = ψ − π

(пп.1, 2, 3), запишем

 

 

 

m

2

 

 

 

 

 

 

 

 

36

 

 

 

 

UR = RI = RIm cos(ωt − ϕ),

 

 

 

 

 

 

 

UC

=

q

=

qm cos(ωt − ψ )

=

Im

cos

ωt − ϕ − π

= Uc

cos ωt − ϕ − π

,

 

 

 

 

 

 

 

 

 

C

C

ωC

 

 

2

 

m

 

2

 

 

 

UL = L dI

= −ωLIm sin (ωt − ϕ) = ωLIm cos ωt − ϕ +

π

= Uc

cos ωt − ϕ +

π

.

 

 

dt

 

 

 

 

 

 

 

 

 

2

m

 

 

2

 

Из последних трех формул видно, что UR находится в фазе с током I,

 

 

UC

отстает по фазе от I на π

, а

UL опережает I на π

. Все это можно

 

 

 

 

 

 

2

 

 

 

 

 

 

2

 

 

 

 

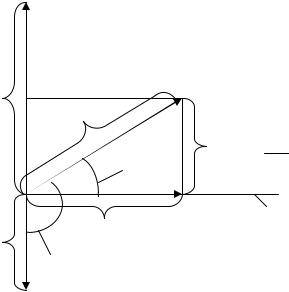
наглядно представить с помощью векторной диаграммы, изобразив ампли-

туды напряжений UR

= RIm, UC

= Im / ωC, UL = ωLIm и их вектор-

m

m

m

ную сумму, равную вектору величины Um (рис. 29.7). (Поскольку UL и UC в противофазе, сначала находим разность U Lm −UCm и вектор этой

разности складываем векторно с U Rm ).

Из прямоугольного треугольника (треугольника напряжений) этой диаграммы легко получить ранее представленное выражение в п. 3 для тангенса разности фаз φ между током I и приложенным напряжением U.

UL

UL

= ωLIm

Um

m

 

ϕ

 

ωL −

1 I

m

=U

Lm

−U

 

 

 

 

Cm

 

 

 

ωC

 

 

 

 

U

Cm

=

1

I

m

U Rm = RIm

U R

Ось тока

 

 

 

ωC

 

 

 

 

 

 

 

 

 

 

ψ

 

 

 

 

 

 

 

 

 

 

UC

Рис. 29.7

 

 

 

 

 

 

 

 

ωL −

1

 

 

 

 

 

 

 

 

 

tgϕ =

ωC

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R

Векторная диаграмма достаточно наглядна и полезна при решении многих конкретных задач.

37

Вопросы для самоконтроля

1.Выведите дифференциальное уравнение гармонических незатухающих колебаний в контуре Томсона.

2.Выведите дифференциальное уравнение затухающих электромагнитных колебаний. Какие характеристики затухающих колебаний вы знаете? Каков их смысл?

3.Каким образом возникают вынужденные электромагнитные колебания? Напишите формулу тангенса угла сдвига по фазе между током и приложенным напряжением.

4.Напишите формулы для полного, индуктивного и емкостного сопротивлений.

5.Как построить векторную диаграмму и треугольник напряжений?

6.В чем, по-вашему, состоит единство колебательной природы механических и электромагнитных колебаний?

38

Лекция № 30

УРАВНЕНИЯ МАКСВЕЛЛА. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ

План

1.Фарадеевская и максвелловская трактовки явления электромагнитной индукции. Ток смещения.

2.Система уравнений Максвелла в интегральной и дифференциальной формах. Электромагнитное поле.

3.Волновые уравнения для электромагнитного поля и их решения. Скорость распространения электромагнитных волн в средах. Основные свойства электромагнитных волн.

4.Энергия и поток энергии электромагнитных волн. Вектор Пойнтинга.

5.Излучение диполя. Диаграмма направленности.

1. Фарадеевская и максвелловская трактовки явления электромаг-

нитной индукции. Ток смещения. Из закона электромагнитной индукции Фарадея следует

εi = -dФ/dt,

где εi - ЭДС электромагнитной индукции; dФ/dt - скорость изменения магнитного потока. В фарадеевской трактовке при изменении магнитного потока, пронизывающего некоторый проводящий контур, в нем возникают ЭДС и индукционный ток. Максвелл предположил, что изменяющееся со временем магнитное поле обусловливает появление в пространстве электрического поля независимо от присутствия в этом пространстве проводящего контура. Наличие контура лишь позволяет обнаружить по возникновению в нем индукционного тока существование в соответствующих точках пространства электрического поля.

Итак, согласно идее Максвелла изменяющееся со временем магнитное поле порождает электрическое поле. Это поле существенно отличается от порождаемого неподвижными зарядами электростатического поля. Электростатическое поле потенциально, его силовые линии начинаются и заканчиваются на зарядах. Электрическое поле, создаваемое переменным магнитным полем, вихревое, его силовые линии замкнуты.

39

В 1865 г. Максвелл высказал гипотезу о том, что изменение электрического поля должно вызывать образование магнитного поля. В дальнейшем эта гипотеза нашла экспериментальное подтверждение.

Переменное электрическое поле, которое может создавать переменное магнитное поле, Максвелл назвал током смещения. (В смысле эквивалентности току проводимости в отношении способности создавать магнитное поле).

Рассмотримцепьпеременноготока, содержащуюконденсатор(рис. 30.1).

(–)+q

 

(+)–q

Между обкладками заряжающегося и разряжающегося

 

 

 

конденсатора имеется переменное электрическое по-

 

 

 

Iле. Когда меняется заряд пластин, в проводнике, связывающем пластины конденсатора, течет электриче-

 

ский ток. Этот ток равен скорости изменения заряда

Рис. 30.1

на конденсаторе

I = dqC .

(1)

 

 

dt

 

Как известно, qC = CUC (С - емкость конденсатора;

UC - напряжение

на нем), C = εε0S / l

(здесь, кроме известных обозначений, l - расстояние

между пластинами конденсатора).

 

 

Напряжение на конденсаторе UC можно представить как произведение напряженности электрического поля внутри конденсатора на расстояние

между пластинами, т.е. UC = Еl,

подставляя в (1), получим

 

 

 

dq

d

 

 

d

εε

 

SEl

 

 

 

I =

 

C

=

 

(CUC ) =

 

 

 

 

0

 

= Sd (εε0E )/ dt .

 

 

dt

 

 

 

 

 

 

 

dt

 

 

dt

 

l

 

Выражение в скобкахεε0E = D – электрическое смещение, т.е.

 

 

 

 

 

 

 

I = S dD .

 

 

 

 

 

 

 

 

 

 

 

 

dt

 

 

Разделим обе части на S, тогда в левой части будет плотность тока

 

I

 

 

dD , т.е. j = dD

 

 

 

 

 

 

G

j =

, а в правой

. Так как в общем случае D может иметь

 

 

S

 

dt

 

dt

 

 

 

 

 

 

 

производные и по координатам, запишем j через частную производную по времени j = ∂∂Dt или в векторной форме

Gj = ∂∂Dt

Эта величина получила название плотности тока смещения. Ток смещения находится интегрированием.

40

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности