Контрольная для заочки 2014(МПП)

Задание 1 к контрольной работе по МПП

Подбор формул по данным опыта методом наименьших квадратов

В практической работе часто зависимость между переменными величинами получается в результате опыта (измерений). Обычно в таком случае эта зависимость оказывается заданной в виде таблицы. Функции, заданные таким образом, могут входить в дальнейшие операции и расчеты.

Для удобства пользования такими зависимостями необходимо сперва подобрать формулу, хорошо описывающую опытные данные. Подбор формулы, описывающей результаты опыта, является существенной частью обработки экспериментальных данных. Одним из методов получения таких формул является способ наименьших квадратов.

Требуется найти зависимость y = f(x). Такой зависимостью может быть:

–линейная,

–степенная,

–показательная,

–логарифмическая,

–гиперболическая и т.д.

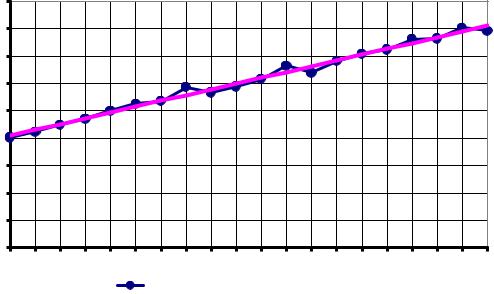
Метод наименьших квадратов позволяет подобрать более точные значения параметров а и b. Предварительно необходимо установить общий вид аналитической функции, который можно выявить по опытным данным, если их нанести на плоскость с координатами X-Y (рис.3).

Зависимость у от х, изображаемая аналитической функцией y = f(x), не может совпадать с экспериментальными значениями во всех n точках. Это означает, что для всех или некоторых точек имеем разность , отличную от нуля.

Метод наименьших квадратов заключается в том, что подбираются параметры a и b таким образом, чтобы сумма квадратов разностей была наименьшей, т.е.

∑ ∑[ ]

Рис. 1. Теоретическая и экспериментальная зависимости

Если вид функции y = f(x) установлен, то ее можно представить в виде

,

где a и b – искомые параметры, тогда

∑[ ]

Для нахождения минимума выражения вычислим частные производные по аргументам a и b и приравняем эти производные к нулю, получим:

систему, найдем значения параметров a и b. При найденных значениях параметров величина z будет наименьшей, т.е. аналитическая зависимость будет

∑

Выбираем числа a и b так, чтобы величина z была наименьшей, для чего вычислив частные производные выражения по a и b, получим

∑

∑

{

Эти два условия дают следующую систему уравнений

∑ ∑ ∑

∑ ∑

{

Откуда

∑∑ ∑

∑∑

∑∑

{

Для определения численной величины параметров a и b составляем расчетную табл. 2 или программу для расчета на ЭВМ.

Таблица 2

Задание

Используя опытные данные (см. вариант задания в приложении), рассчитать коэффициенты регрессии с помощью ручного счета. Привести графики теоретической и экспериментальной зависимостей.

Задание 2 к контрольной работе по МПП

ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Задачи, возникающие при изучении процессов автомобильного транспорта, требуют знаний основных положений теории вероятностей и математической статистики.

Если математическая статистика изучает методы сбора и обработки результатов наблюдений случайных процессов, то теория вероятностей изучает их закономерности.

Случайные процессы – это такие процессы, которые при неоднократном воспроизведении одного и того же опыта протекают каждый раз несколько по другому.

При решении задач математической статистики и теории вероятностей приходится сталкиваться с понятием генеральной и выборочной совокупностей.

Генеральной совокупностью называют совокупность всех объектов (элементов), подлежащих изучению. Очевидно, что подвергать исследованию всю генеральную совокупность затруднительно или нецелесообразно. В связи с этим из генеральной совокупности извлекают лишь некоторую ее часть, называемую выборочной совокупностью (выборкой).

При изучении процессов автомобильного транспорта нередко возникает необходимость обработки больших объемов информации, представленной в виде статистических рядов. Например, пробег шин до замены, величина износа протектора шины у различных автомобилей на определенном пробеге, величина лифта рулевого управления автомобилей в процессе эксплуатации и т.д.

При обработке таких статистических рядов определяются его числовые характеристики, к которым относятся:

–среднее арифметическое случайной величины (выборочное среднее);

–статистическая дисперсия;

–среднеквадратическое отклонение;

–коэффициент асимметрии, эксцесса, вариации и т.д.

Числовые характеристики статистического ряда

Среднее арифметическое случайной величины служит характеристикой математического ожидания распределения случайной величины и вычисляется по формуле

относительно ее среднего значения (математического ожидания). Она вычисляется по формуле

∑( )

Среднее квадратическое отклонение служит мерой рассеивания случайной величины относительно ее среднего значения и вычисляется по формуле

коэффициенту вариации приближенно определяется закон распределения случайной величины, так при V < 0,3 распределение подчиняется нормальному закону, при V = 0,52 – закону распределения Релея, а при, V= 1,0 – экспоненциальному (показательному) закону распределения.

Статистическая оценка коэффициента асимметрии дает дополнительную информацию о форме распределения случайной величины. Асимметрия или скошенность вычисляется по формуле

∑( )

Статистическая оценка коэффициента эксцесса также дает дополнительную информацию о форме распределения случайной величины. Эксцесс, или островершинность вычисляется по формуле

Для нормального закона асимметрия и эксцесс равны нулю.

Используя методы математической статистики, возможно определить числовые характеристики выборочной совокупности. И перенеся их по определенным правилам на генеральную совокупность, оценить числовые характеристики последней.

Построение интервального вариационного ряда

Вариационным рядом называют представление статистических данных позволяющих судить о частоте распределяемого признака.

Например:

3, 4, 5, 2, 2, 3, 3, 4, 5, 3 – статистический ряд

2, 2, 3, 3, 3, 3, 4, 4, 5, 5 – ранжированный статистический ряд 2, 4, 2, 2 – вариационный ряд

Пусть имеем доброкачественный объём выборки (статистический ряд). Порядок обработки его следующий:

– зарегистрированные значения рассматриваемого признака Xi расположить в

–определить размах измерения значений параметра R = Xmax – Xmin;

–вычислить число интервалов К в зависимости от объёма выборки n

К= 1 + 3,32 lg n;

–определить ширину частичного интервала h:

;

– определить границы интервалов, для чего установить нулевое (крайнее) значение интервала X0:

X0 = Xmin – h/2.

Следующие границы интервалов определяются последовательным прибавлением ширины интервала h к предыдущему значению границы:

X1 = X0 + h, X2 = X1 + h и т.д. до тех пор, пока Xi не будет больше Xmax;

–определить число элементов значений признаков, попавших в i-й интервал (эту величину называют опытной частотой mi* данного интервала);

–определить относительную величину частоты (частость) i-го интервала Wi:

Wi = mi/n;

– определить накопленную частость Wiн

∑

Накопление частости Wн получается путём последовательного прибавления частости Wi очередного интервала: , , , и т.д., для последнего интервала Wnн = 1;

– результаты расчёта свести в таблицу:

Основные числовые характеристики вычисляются по следующим формулам:

– среднее арифметическое:

∑ ∑

– статистическая дисперсия:

– среднее квадратическое отклонение:

√

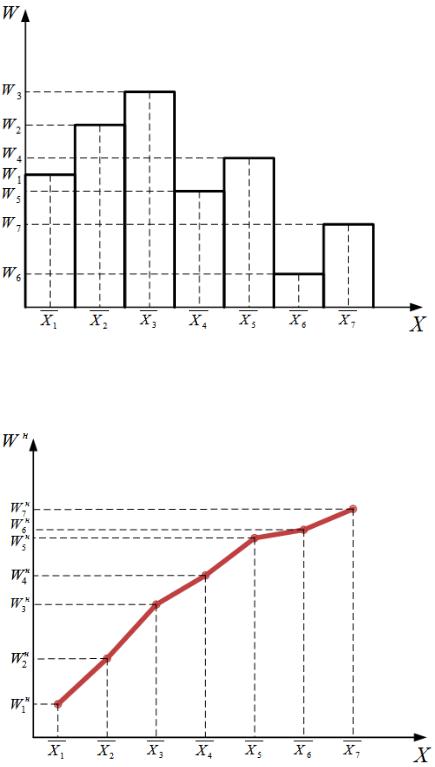
Графическое выражение закона распределения можно представить в виде

Рис. 1. Гистограмма распределения признака

Рис. 2. Кумулятивная кривая

Задание

По представленной выше методике обработать статистический ряд (см. вариант задания в приложении), определить основные числовые характеристики (с помощью ручного счета). Привести графики гистограммы распределения признака и кумулятивной кривой.

Примечание: все результаты вычислений округлять до тысячных (три цифры после запятой).

Варианты заданий к выполнению контрольной работы № 1