Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых»

(ВлГУ)

кафедра «Функциональный Анализ и его Приложения»

Контрольная работа

по дисциплине: Исследования операций в экономике.

Вариант 9

Выполнила:

Сапожкова Д. В.

Группа: ЗЭКсд-112

Принял:

Беспалов М.С.

Владимир – 2013г.

Задача 1. Решить задачу линейного программирования.

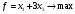
при условиях

.

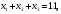
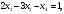
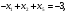
Решение

Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.

Поскольку в правой части присутствуют отрицательные значения, умножим соответствующие строки на (-1).

Определим максимальное значение целевой функции F(X) = x₁ + 3x₃ при следующих условиях-ограничений.

x₁ + x₂ + x₃=11

2x₁ - 3x₂ - x₄=1

x₁ - x₂ - x₅=3

Введем искусственные переменные x: в 1-м равенстве вводим переменную x₆; в 2-м равенстве вводим переменную x₇; в 3-м равенстве вводим переменную x₈;

1x₁ + 1x₂ + 1x₃ + 0x₄ + 0x₅ + 1x₆ + 0x₇ + 0x₈ = 11

2x₁-3x₂ + 0x₃-1x₄ + 0x₅ + 0x₆ + 1x₇ + 0x₈ = 1

1x₁-1x₂ + 0x₃ + 0x₄-1x₅ + 0x₆ + 0x₇ + 1x₈ = 3

Для постановки задачи на максимум целевую функцию запишем так:

F(X) = x₁+3x₃ - Mx₆ - Mx₇ - Mx₈ → max

Из уравнений выражаем искусственные переменные:

x₆ = 11-x₁-x₂-x₃

x₇ = 1-2x₁+3x₂+x₄

x₈ = 3-x₁+x₂+x₅

которые подставим в целевую функцию:

F(X) = (1+4M)x₁+(-3M)x₂+(3+M)x₃+(-M)x₄+(-M)x₅+(-15M) → max

Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:

1	1	1	0	0	1	0	0
2	-3	0	-1	0	0	1	0
1	-1	0	0	-1	0	0	1

Решим систему уравнений относительно базисных переменных:

x₆, x₇, x₈,

Полагая, что свободные переменные равны 0, получим первый опорный план:

X1 = (0,0,0,0,0,11,1,3)

Базис	B	x1	x2	x3	x4	x5	x6	x7	x8
x6	11	1	1	1	0	0	1	0	0
x7	1	2	-3	0	-1	0	0	1	0
x8	3	1	-1	0	0	-1	0	0	1
F(X0)	-15M	-1-4M	3M	-3-M	M	M	0	0	0

Переходим к основному алгоритму симплекс-метода.

Итерация №0.

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.

В качестве ведущего выберем столбец, соответствующий переменной x₁, так как это наибольший коэффициент по модулю.

Вычислим значения D_i по строкам как частное от деления: b_i / a_i1

и из них выберем наименьшее:

Следовательно, 2-ая строка является ведущей.

Разрешающий элемент равен (2) и находится на пересечении ведущего столбца и ведущей строки.

Базис	B	x1	x2	x3	x4	x5	x6	x7	x8	min
x6	11	1	1	1	0	0	1	0	0	11
x7	1	2	-3	0	-1	0	0	1	0	1/2
x8	3	1	-1	0	0	-1	0	0	1	3
F(X1)	-15M	-1-4M	3M	-3-M	M	M	0	0	0	0

Получаем новую симплекс-таблицу:

Базис	B	x1	x2	x3	x4	x5	x6	x7	x8
x6	101/2	0	21/2	1	1/2	0	1	-1/2	0
x1	1/2	1	-11/2	0	-1/2	0	0	1/2	0
x8	21/2	0	1/2	0	1/2	-1	0	-1/2	1
F(X1)	1/2-13M	0	-11/2-3M	-3-M	-1/2-M	M	0	1/2+2M	0

Итерация №1.

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.

В качестве ведущего выберем столбец, соответствующий переменной x₂, так как это наибольший коэффициент по модулю.

Вычислим значения D_i по строкам как частное от деления: b_i / a_i2

и из них выберем наименьшее:

Следовательно, 1-ая строка является ведущей.

Разрешающий элемент равен (2¹/₂) и находится на пересечении ведущего столбца и ведущей строки.

Базис	B	x1	x2	x3	x4	x5	x6	x7	x8	min
x6	101/2	0	21/2	1	1/2	0	1	-1/2	0	41/5
x1	1/2	1	-11/2	0	-1/2	0	0	1/2	0	-
x8	21/2	0	1/2	0	1/2	-1	0	-1/2	1	5
F(X2)	1/2-13M	0	-11/2-3M	-3-M	-1/2-M	M	0	1/2+2M	0	0

Получаем новую симплекс-таблицу:

Базис	B	x1	x2	x3	x4	x5	x6	x7	x8
x2	41/5	0	1	2/5	1/5	0	2/5	-1/5	0
x1	64/5	1	0	3/5	-1/5	0	3/5	1/5	0
x8	2/5	0	0	-1/5	2/5	-1	-1/5	-2/5	1
F(X2)	64/5-2/5M	0	0	-22/5+M	-1/5-2/5M	M	3/5+11/5M	1/5+12/5M	0

Итерация №2.

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.

В качестве ведущего выберем столбец, соответствующий переменной x₄, так как это наибольший коэффициент по модулю.

Вычислим значения D_i по строкам как частное от деления: b_i / a_i4

и из них выберем наименьшее:

Следовательно, 3-ая строка является ведущей.

Разрешающий элемент равен (²/₅) и находится на пересечении ведущего столбца и ведущей строки.

Базис	B	x1	x2	x3	x4	x5	x6	x7	x8	min
x2	41/5	0	1	2/5	1/5	0	2/5	-1/5	0	21
x1	64/5	1	0	3/5	-1/5	0	3/5	1/5	0	-
x8	2/5	0	0	-1/5	2/5	-1	-1/5	-2/5	1	1
F(X3)	64/5-2/5M	0	0	-22/5+M	-1/5-2/5M	M	3/5+11/5M	1/5+12/5M	0	0

Получаем новую симплекс-таблицу:

Базис	B	x1	x2	x3	x4	x5	x6	x7	x8
x2	4	0	1	1/2	0	1/2	1/2	0	-1/2
x1	7	1	0	1/2	0	-1/2	1/2	0	1/2
x4	1	0	0	-1/2	1	-21/2	-1/2	-1	21/2
F(X3)	7	0	0	-21/2	0	-1/2	1/2+M	M	1/2+M

Итерация №3.

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.

В качестве ведущего выберем столбец, соответствующий переменной x₃, так как это наибольший коэффициент по модулю.

Вычислим значения D_i по строкам как частное от деления: b_i / a_i3

и из них выберем наименьшее:

Следовательно, 1-ая строка является ведущей.

Разрешающий элемент равен (¹/₂) и находится на пересечении ведущего столбца и ведущей строки.

Базис	B	x1	x2	x3	x4	x5	x6	x7	x8	min
x2	4	0	1	1/2	0	1/2	1/2	0	-1/2	8
x1	7	1	0	1/2	0	-1/2	1/2	0	1/2	14
x4	1	0	0	-1/2	1	-21/2	-1/2	-1	21/2	-
F(X4)	7	0	0	-21/2	0	-1/2	1/2+M	M	1/2+M	0

Получаем новую симплекс-таблицу:

Базис	B	x1	x2	x3	x4	x5	x6	x7	x8
x3	8	0	2	1	0	1	1	0	-1
x1	3	1	-1	0	0	-1	0	0	1
x4	5	0	1	0	1	-2	0	-1	2
F(X4)	27	0	5	0	0	2	3+M	M	-2+M

Конец итераций: индексная строка не содержит отрицательных элементов - найден оптимальный план

Окончательный вариант симплекс-таблицы:

Базис	B	x1	x2	x3	x4	x5	x6	x7	x8
x3	8	0	2	1	0	1	1	0	-1
x1	3	1	-1	0	0	-1	0	0	1
x4	5	0	1	0	1	-2	0	-1	2
F(X5)	27	0	5	0	0	2	3+M	M	-2+M

Оптимальный план можно записать так:

x₃ = 8

x₁ = 3

x₄ = 5

x₂ = 0

x₅ = 0

F(X) = 3•8 + 1•3 + 0•5 = 27

Задача 2. Сформулировать двойственную задачу к задаче 1 и решить ее.

Решение

Составим двойственную задачу к прямой задаче.

y₁ + 2y₂ - y₃≥1

y₁ - 3y₂ + y₃≥0

y₁≥3

- y₂≥0

y₃≥0

11y₁ + y₂ - 3y₃ → min

Решение двойственной задачи дает оптимальную систему оценок ресурсов.

Используя последнюю итерацию прямой задачи найдем, оптимальный план двойственной задачи.

Из теоремы двойственности следует, что Y = C*A^-1.

Составим матрицу A из компонентов векторов, входящих в оптимальный базис.

Определив обратную матрицу D = А^-1 через алгебраические дополнения, получим:

Как видно из последнего плана симплексной таблицы, обратная матрица A^-1 расположена в столбцах дополнительных переменных.

Тогда Y = C*A^-1 =

Оптимальный план двойственной задачи равен:

y₁ = 3

y₂ = 0

y₃ = 2

Z(Y) = 11*3+1*0+-3*2 = 27

Задача 3. Решить задачу линейного программирования двумя методами:

графически в трехмерном пространстве и симплекс-методом.

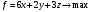
при условиях

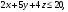
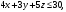
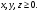
Решение

Запишем задачу в виде основной задачи линейного программирования

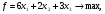
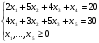
Решим задачу симплексным методом

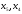- базисные переменные

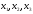- свободные переменные

начальное решение (0; 0; 0; 20; 30).

Б	З	х1	х2	х3	х4	х5
х4	20	2	5	4	1	0
х5	30	4	3	5	0	1
f	0	-6	-2	-3	0	0

Поскольку в f-ой строке есть отрицательные элементы, то начальное решение не оптимально. Выбираем первый столбец в качестве ведущего. х₁ перейдёт в базис - покинет базис.

Б	З	х1	х2	х3	х4	х5
х4	5	0	7/2	3/2	1	-1/2
х1	15/2	1	3/4	5/4	0	1/4
f	45	0	5/2	9/2	0	3/2

Поскольку в f-ой строке нет отрицательных элементов, то решение оптимально.

Получаем следующий план:

z=x₃ = 0

x=x₁ = 7.5

y=x₂ = 0

f = 6•7.5 + 2•0 + 3•0 = 45

Задача 4. Решить транспортную задачу, для которой задана матрица стоимостей перевозок с указанными запасами и потребностями. Предварительно выяснить -- открытой или закрытой является задача.

Указание. Начальный план выбираем по методу северо-западного угла или минимальной стоимости. Оптимизацию следует проводить методом потенциалов.

	В1	В2	В3	В4	запасы
А1	5	3	2	3	100
А2	3	5	4	3	200
А3	4	2	3	7	150
А4	8	6	7	2	150
потребности	170	80	140	190