4.2. Графы как модели программ, данных и процессов

Управляющие графы. Многие задачи анализа программ, возникающие при их оптимизации, трансляции, проверке правильности, тестировании и т. д., значительно упрощаются, если их рассматривать на теоретико-графовых моделях. Базисной моделью является управляющий граф программы. Орграф G = (X, U) называется управляющим графом (р-графом, графом переходов), если выполнены следующие условия:

а) граф G не содержит параллельных дуг;

б) в множестве вершин графа выделена одна вершина S — вход графа;

в) в множестве верщин графа выделена хотя бы одна вершина —выход графа;

г) каждая вершина достижима из входа s;

д) каждая вершина достигает выхода t.

Замечание. Можно считать, что в управляющем графе имеется более чем один выход, поскольку этот случай легко сводится к случаю одного выхода введением фиктивного выхода, соединенного дугами с каждым фактическим выходом. В большинстве случаев можно считать, что полустепень исхода каждой вершины, отличной от входа и выхода, равна 1 или 2, а полустепень исхода входа равна 1.

Построение управляющего графа для конкретной программы производится по простым правилам с требуемой степенью детальности (и, как правило, автоматически). Тривиальное решение задачи состоит в изображении каждого оператора языка (команды, строки или любого фрагмента, признаваемого единицей языка) в виде отдельной вершины. При этом две вершины смежны, если между соответствующими операторами имеется передача управления. При этом оператор, после исполнения которого производится передача управления, представляется началом дуги; оператор, на который передается управление, ‑ концом дуги, а каждая передача управления ‑ дугой. При таком подходе размер графа сильно растет за счет появления длинных цепочек вершин, соответствующих линейным участкам программ. Они могут быть представлены одной вершиной.

Ордерево как форма организации динамических словарей. Пусть на вход некоторой программы подается некоторый текст и требуется составить список всех различных слов, встречающихся в тексте. Эта задача может быть усложнена требованием предоставления возможности пользоваться списком до включения в него всех слов. Кроме того, неизвестно обш;ее число слов в тексте. Для решения задачи с достаточной эффективностью требуется структура, которую можно было бы просмотреть за время, меньшее, чем потребовалось бы для неупорядоченного списка слов, и которая обладала бы еш;е одним свойством: вписывание новых слов не должно вызывать затруднений. Такой структурой служит корневое упорядоченное дерево в виде бинарного (или -арного) дерева сортировки — бинарного дерева, снабженного метками, взятыми из множества меток с введенным на нем отношением полной упорядоченности, и такого, что все метки из левого поддерева любой вершины меньше метки в этой вершине, а меток в правом поддереве — соответственно больше.

Включение нового слова соответствует подвешиванию к дереву новой вершины, меткой которой было бы новое слово, без нарушения свойства дерева быть бинарным. Для отыскания места подвешивания новой вершины будем двигаться, начиная с корня и сравнивая включаемое слово с метками проходимых вершин: если метка совпадает с включаемым словом, то ничего делать не надо, так как слово уже в словаре; если метка больше нового слова, то движемся к потомку вершины по левой дуге, в противном случае—по правой.

Если слова в словаре нет, то мы попадаем в вершину, у которой отсутствует один или оба потомка; к ней и подвешиваем новую вершину.

Граф-модель вычислительного процесса. Пусть дана некоторая формула, или задача, состоящая из ряда подзадач, или совокупность задач, использующих одни и те же ресурсы, и т. п. Для простоты будем говорить о вычислении некоторой формулы. Порядок вычислений может существенно влиять на объем требуемой для хранения исходных и промежуточных данных оперативной памяти. Изобразим формулу в виде каскадного информационного графа. В нем каждая внутренняя вершина соответствует оператору; это означает, что в эту вершину входит столько дуг, сколько аргументов у оператора, а выходит одна дуга, представляющая результат вычислений. Вводимым данным будут соответствовать вершины, из которых исходит только одна дуга и ни одна дуга не входит, ‑ входы графа.

Пример. Рассмотрим пример изображения формулы в виде ордерева.

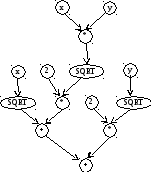
Отсюда следует, что каскадный информационный граф представляет собой корневое ордерево, в котором корень соответствует вычисляемому результату. В качестве веса вершины в такой модели вычислительного процесса выступает требуемый объем памяти.

Граф-модель информационно-логической системы. Среди исходных данных, необходимых для выбора структуры комплекса вычислительных средств (КВС), важнейшую роль играют сведения о множестве задач, решаемых системой. Простейшей формой задания такого множества является перечень задач; следующей по сложности формой является комплект алгоритмов решения задач системы. Наиболее развитой и совершенной формой задания вычислительной работы системы является информационно-логическая структура (ИЛС) системы, под которой понимается совокупность алгоритмов, увязанных в единое целое по перерабатываемой информации, для решения общей главной задачи системы.

Описание ИЛС системы должно включать в себя не только перечень алгоритмов, но и указания о последовательности их реализации, об их характеристиках и об исходной информации. Наиболее удобная форма описания ИЛС ‑ представление ее в виде орграфа алгоритмов.

Такие графы позволяют не только выявлять свойства ИЛС, но и решать следующие важные практические задачи:

— установление рационального порядка разработки алгоритмов;

— перечисление возможных вариантов привязки алгоритмов к пунктам обработки информации;

— составление исходных матриц, необходимых для оптимизации KBС по показателям качества КВС;

— упрощение ИЛС системы;

— составление управляющих (диспетчерских) алгоритмов.

Графом алгоритмов системы называется орграф , вершиныкоторого изображают частные реализации-х алгоритмов системы. Две вершиныисоединяются дугой, если алгоритмможет реализоваться только вслед за алгоритмом.

Вершинам графа алгоритмов приписывается вес, оценивающий реализацию этих алгоритмов, например число операций , требуемых для реализации-го алгоритма, времяреализации алгоритмана компьютере, число ошибок определения тех или иных величин в результате реализации-го алгоритма и т. д.

В ИЛС системы управления соотношения следования между алгоритмами обычно соответствуют направлениям потоков информации, которые циркулируют в системе при реализации алгоритмов. В самом деле, соотношение (алгоритмследует за) однозначно утверждает, что для реализациинеобходима некоторая входная информация, которая получается в результате реализации алгоритма. Вследствие этого в графах алгоритмов не только вершинам, но и дугам могут быть приписаны вполне определенные веса, поскольку дуги описывают направленные потоки информации между последовательными алгоритмами, описываемые ее составом, объемом и точностными характеристиками. В некоторых случаях дугам графа приписана вероятностьперехода от вершины к вершине .

Графы как объекты обработки информации

Представление графов в памяти компьютера

Представление графов в памяти компьютера существенно зависит от типов структур данных, допускаемых используемым алгоритмическим языком и типом компьютера. Представление с помощью матрицы смежности ‑ одно из самых распространенных. Для графов с большим числом дуг это достаточно компактное представление, особенно если есть возможность работать с двоичными битами в машинном слове. К недостаткам следует отнести большой расход памяти при работе с графами, имеющими небольшое число дуг (матрица смежности при этом получается весьма разреженной), а также невозможность уменьшения трудоемкости алгоритмов в том случае, когда она пропорциональна числу дуг, а не числу вершин.

Матрица смежности неориентированного графа симметрична относительно главной диагонали, поэтому достаточно хранить в памяти только половину ее.

Задание графа с помощью матрицы смежности удобно и тогда, когда граф взвешенный и элементами матрицы являются не нули и единицы, а веса дуг. Пример задания ориентированного и неориентированного графов матрицами смежности приведен на рис. 4.2.

Рис. 4.2. Задание ориентированного и неориентированного графов матрицами смежности.

Представление с помощью матрицы инциденций определяет граф однозначно (с точностью до изоморфизма), но применяется крайне редко в силу большой разреженности матрицы и практического отсутствия алгоритмов, работающих на такой структуре данных.

Представление с помощью списков смежности является основной альтернативой представлению с помощью матрицы смежности. Список смежности для вершины v ‑ это список концов дуг, исходящих из вершины в случае орграфа, или список смежных свершин в случае графа. Граф представляется с помощьюсписков смежности, по одному для каждой вершины. Если число дуг в орграфе существенно мало по сравнению с полным графом, то этот сподоб представления весьма эффективен. Списки смежности занимают объем памятии легко реализуются с помощью списочных структур. Менее удобен этот способ представления для задания взвешенных графов, так как тогда возникает необходимость хранения весов дуг и установления соответствующих связей между дугами и их весами.

Пример задания графов, показанных на рис. 4.2, с помощью списков смежности приведен на рис. 4.3. Представление с помощью списка дуг применяется в тех случаях, когда необходимо иметь отдельную, независимую нумерацию дуг. При этом способе каждой дуге сопоставляется тройка , где‑ дуга,‑ ее начало,‑ ее конец. Этот способ представления легко обобщается на случай взвешенных графов. Более того, он наиболее приспособлен для хранения различной информации о дугах.

Пусть ‑ неориентированный граф,‑ его матрица смежности. Так каксимметрична относительно главной диагонали, будем рассматривать только ее верхнюю треугольную часть. Запишем строкипоследовательно одну за другой и найдем двоичное число, соответствующее полученной последовательности из нулей и единиц. Меняя нумерацию вершин, будем для одного и того же графа получать разные числа. Наибольшее из них носит названиекода Xapapи.

Рис. 4.3. Списки смежности графов на рис. 4.2.

Код Харари определяет граф однозначно, поэтому, например, задачу определения изоморфизма двух графов можно свести к сравнению соответствующих кодов Харари³.

Нумерация вершин (и матрица смежности), соответствующая коду Харари, носит название канонической и используется при перечислении (генерировании) графов с заданными свойствами.

Наиболее распространенным методом сбора информации о строении графа является специальным образом организованный обход вершин и дуг (ребер) графа [5]. Информация, получаемая таким способом, оформляется в виде подходящей нумерации вершин.

Нумерации, выявляющие логическую структуру графа

Определение 4.22 [5]. Нумерацией вершин графаназывается инъективное отображение множества вершинграфа в множествонатуральных чисел,⁴.

Пусть ‑ некоторая нумерация. Номер вершиныв нумерацииобозначается, а множество последовательно занумерованных в нумерациивершин или последовательно-занумеровапных вершин—черезили через, гдеи. Дугуназовем обратной дугой относительно нумерации, если.

Применение методов теории графов к организации вычислительного процесса

Размещение блоков программы в оперативной памяти компьютера: сведение к задаче коммивояжера. Пусть ‑ отдельные блоки программы, и пусть‑ вероятность исполнения блокапосле. Если‑ первый блок, а‑ последний, то положимЕсли марковский процесс, описываемый матрицей переходов, является эргодическим, т. е. для него существует предельное распределение, которое не зависит от начального состояния процесса, то частоты исполнения отдельных блоковудовлетворяют матричному уравнению, нормализованному так, что сумма частот исполнения равна 1. Пусть величинынайдены. Тогда, если‑ время исполнения блока, то ожидаемое время исполнения всей программы равно. Еслииизвестны, то можно рассмотреть задачу минимизации ожидаемого числа передач управления, производимых при выполнении программы. Если блокследует в памяти за блоком, то передача управления нужна всякий раз, когда после блокавыполняется блок, отличный от. Ожидаемое число таких передач равно.

Пусть , если блокнепосредственно следует за блокомв памяти, ив противном случае.

Пусть ‑ блок, состоящий из кодов начальных данных и кодов, которые не выполняются в виде команд. Тогда для всехимеем. Полагаем, если‑ погледний блок в памяти, и, если— первый блок в памяти, в остальных случаях полагаем, Тогда рассматриваемая задача сводится к минимизации ожидаемого числа выполнения передач управленияпри условии, что есть матрица циклической перестановки, а это и есть задача коммивояжера (см. раздел 6.2.3).

Рассмотрим ситуацию, когда на входе компьютера ямеется некоторое множество задач, имеющих общие страницы в памяти. Требуется определить такую последовательность решения этих задач, чтобы минимизировать пересылки страниц памяти. Для решения построим граф, вершинам которого будут соответствовать задачи, а две вершины соединены ребром тогда и только тогда, когда они соответствуют задачам, имеющим общие страницы памяти. Каждому ребру сопоставляется вес, зависящий от числа общих страниц.

Тогда проблема активизации задач сводится к отысканию оптимального каркаса графа активизации. Особенность этой проблемы состоит в том, что чаще всего стоимость каркаса ‑ нелинейная функция от весов ребер.

Поиск в глубину в графе

Идея метода поиска в глубину⁵ состоит в следующем. Поиск в обыкновенном графе начинается с некоторой начальной вершины(с этого моментасчитается просмотренной). Пусть‑ последняя просмотренная вершина (этой вершиной может быть и). Тогда возможны два случая.

1) Среди вершин, смежных с , существует еще непросмотренная вершина. Тогдаобъявляется просмотренной, и поиск продолжается из вершины. Будем говорить, что вершинаявляетсяотцом вершины (). Ребров этом случае будет называтьсядревесным.

2) Все вершины, смежные с , просмотрены. Тогда и объявляетсяиспользованной вершиной. Обозначим через ту вершину, из которой мы попали в, т. е.; ноиск в глубину продолжается из вершины.

Если в графе не осталось непросмотренных вершин, то поиск заканчивается. Если же осталась непросмотренная вершина, то поиск продолжается из этой вершины.

Поиск в глубину просматривает вершины графа в определенном порядке. Для того чтобы зафиксировать этот порядок, будет использоваться массив. При этом естественно считать, что, еслиначальная вершина, и, еслипросматривается сразу после того, как просмотрена вершина.

Пусть в обыкновенном графе проведен поиск в глубину. Обозначим черезмножество всех древесных ребер. Все остальные ребра графа будем называтьобратными ребрами. Множество всех обратных ребер обозначим через .

Результат применения поиска в глубину к связному графу (рис.4.4 а) показан на рис. 4.4b. Здесь сплошные линии изображают древесные ребра, а пунктирные линии ‑ обратные ребра.

Рис. 4.4. a) Связный граф; b) Результат применения поиска в глубину к связному графу.

Нумерация вершин соответствует порядку, в которым они просматриваются поиском в глубину. Можно заметить, что множество всех древесных ребер с выделенной начальной вершиной образует корневое дерево с корнем, которое дерево часто называютглубинным деревом или -деревом графа [5]. Отметим, что каждое обратное ребро соединяет в-дереве предка и потомка.

Отметим несколько свойств поиска в глубину, введя предварительно два определения. Будем называть дуги, пройденные при поиске в глубину дважды (в прямом и обратном направлениях), отмеченными, а путь из начала обходав текущую вершину, не содержащий отмеченных дуг,—текущим путем.

Свойство 1. После завершения обхода орграфа при поиске в глубину частичный граф, образованный отмеченными дугами, есть корневое ордерево с корнем в начале обхода.

Свойство 2. Для того, чтобы после завершения обхода орграфа при поиске в глубину все вершины оказались пройденными, необходимо и достаточно, чтобы обход начинался во входе и этот вход был единственным. При этом корневое ордерево, образованное отмеченными дугами, имеет множество вершин, совпадающее со всем множеством вершин графа, и тем самым является каркасом графа, называемым деревом поиска в глубину.

Свойство 3. Текущий путь есть простой путь в орграфе. Его можно продолжить либо до тупикового, т. е. заканчивающегося висячей вершиной, либо до циклического, т, е. до встречи с уже пройденной вершиной.

Пусть ‑ несвязный граф,‑ множество всех его компонент связности. Обозначим черезмножество древесных ребер, выделенных поиском в глубину в компоненте, а через‑ корневую вершину из, т.е. первую просмотренную вершину подграфа. Таким образом, множество всех древесных ребер несвязного графа образует остовный лес. Фиксируя в каждом поддереве этого леса корневую вершину, мы получимглубинный лес или -лес графа.

Представим теперь формальное описание указанного алгоритма. В алгоритме используются описанные ранее массивы иВ процессе работы алгоритма массивиспользуется для распознавания непросмотренных вершин, а именно, равенствоозначает, что вершинаеще не просмотрена.

Изложим версию алгоритма поиска в глубину, основанную на рекурсивной процедуре ⁶, осуществляющей поиск в глубину из вершины .

Алгоритм поиска в глубину.

1. procedure DFS(v);

2. begin

3. num[v] := i; i := i + 1;

4. for do

5. if then

6. begin

7. ; father[u] := v; DFS(u)

8. end

9. else if num[u] < num[v] and then

10.

11. end;

12. begin

13. i := 1; ;

14. for do ;

15. for do

16. if then

17. begin

18. DFS(v)

19. end

20. end.

4.1.3. Задачи о покрытиях графов.

Задача о реберном покрытии.

Определение 4.23. Множество ребер образуетреберное покрытие графа , если каждая вершинаинцидентна хотя бы одному из ребер множества.

Покрытие с минимальным числом ребер называется минимальным (оптимальным).

Рассмотрим простой пример графа, изображенного на рис. 4.5.

В этом примере ,, номера ребер указаны на рисунке в кружочках. Множество реберне образует реберное покрытие, так как вершины 2 и 5 не инцидентны ни одному из ребер этого одному из ребер этого множества. Множество ребер (1, 4, 6) образует реберное покрытие.

Рис. 4.5. Пример графа.

Матрица инциденций графа имеет вид

	1	2	3	4	5	6	7
1	1	1	1
2	1						1
3		1				1	1
4			1		1	1
5				1	1

Сформулируем модель целочисленного программирования для поиска минимального покрытия графа. Введем бинарных переменных:

.

Тогда целевая функция имеет вид

,

условия инцидентности для всех вершин запишутся в виде

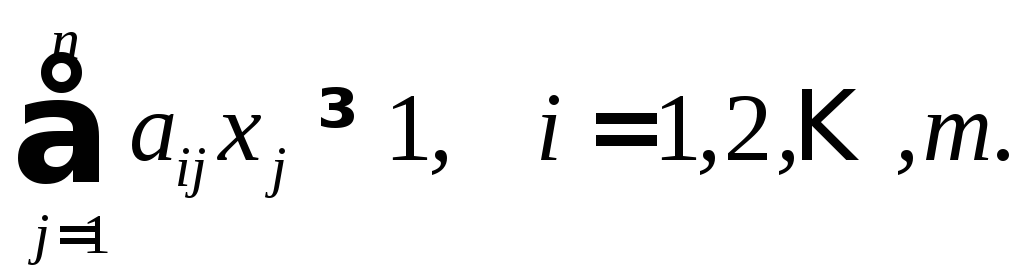
В задаче о взвешенном реберном покрытии каждое ребро характеризуется весом. В этой задаче целевая функция имеет вид

(4.1)

Задача о паросочетаниях. Пусть число вершин графа четно. Под паросочетанием (совершенным) понимается такое множество попарно несмежных ребер, что каждая вершина графа инцидентна одному ребру из этого множества.

Если паросочетание существует, то число ребер в нем равно . Оптимальным называется паросочетание с минимальной суммой весов входящих в него ребер. Целевая функция в задаче о паросочетаниях имеет вид (4.1), а ограничения имеют вид:

Здесь

.

Задача об оптимальном реберном покрытии разрешима для любого связного симметричного графа. В то же время задача о паросочетаниях разрешима не всегда. В частности, она может оказаться неразрешимой, если степени всех вершин нечетны. Но если задача о паросочетаниях разрешима, то ее оптимальное решение есть допустимое решение задачи о реберном покрытии. Поэтому значение целевой функции для оптимального решения задачи о паросочетаниях является верхней оценкой для оптимального решения задачи о реберном покрытии.

Задача о вершинном покрытии.

Определение 4.24. Множество вершин образуетвершинное покрытие графа , если каждое реброинцидентно хотя бы одной вершине из множества. Покрытие с минимальным числом вершин называется минимальным (оптимальным).

На рис. 4.5 множество вершин (3, 4) не образует покрытие, так как ни одно из ребер множества (1, 4) не инцидентно какой-либо из вершин множества (3, 4). Множество вершин (1, 3, 4) образует покрытие.

Сформулируем модель поиска минимального взвешенного покрытия графа в виде задачи целочисленного программирования. Введем бинарных переменных:

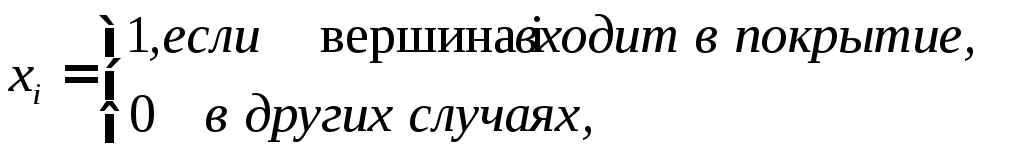
Тогда целевая функция имеет вид

,

условия инцидентности для всех ребер запишутся в виде

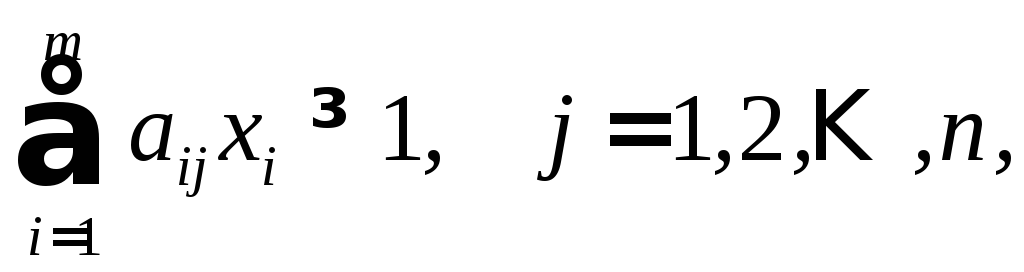
В задаче о взвешенном вершинном покрытии каждой вершине отнесен вес. В этом случае целевая функция имеет вид

,

ограничения – те же.

4.1.4. Задача об изоморфизме графов.

Рассмотрим графы и;. Говорят, что эти графыизоморфны, если можно установить взаимно однозначное соответствие между их вершинами и ребрами так, что если вершины графасоответствуют вершинамграфа, то ребро, если оно существует, соответствует ребру, если оно существует. Если ребросоответствует ребру, то вершинысоответствуют вершинам. Из данного определения следует, что изоморфные графы отличаются лишь нумерацией их вершин.

Рассмотрим простой пример (рис. 4.6). Способ перенумерации задается подстановкой

,

причем в первой строке указаны вершины графа , а во второй ‑ соответствующие им вершины графа, при этом соответствие ребер имеет вид

Рис. 4.6. Изоморфные графы.

В общем случае для изоморфных графов требуется указать подстановку

, (4.2)

в которой вершине графасоответствует вершинаграфатаким образом, чтобы выполнялось соответствие ребер.

Сформулируем задачу об изоморфизме графов в терминах целочисленного программирования. Пусть и‑ матрицы смежности графовисоответственно. Как известно[Kristof], для изоморфизма этих графов необходимо и достаточно существование такой невырожденной матрицы , имеющей одну единицу в каждой строке и каждом столбце, чтобы выполнялось условие

⁷(4.3)

Условие (4.3) перепишем в виде

, (4.4)

что равносильно следующим условиям:

.

Задача о поиске матрицы сводится к минимизации функции

при условиях

Если графы иизоморфны, то минимальное значение функции равно нулю и матрица определяется через подстановку(4.2) следующим образом:

а все остальные ее элементы равны нулю. В нашем примере , если вершинав графеимеет номерв графе:

	1	2	3	4	5
1	0	0	0	0	1
2	0	1	0	0	0
3	0	0	0	1	0
4	1	0	0	0	0
5	0	0	1	0	0

Рассмотрим другие целевые функции в задаче об изоморфизме графов:

.

Эта целевая функция, в отличие от , не является дифференцируемой.

Обратим внимание на то, что каждая из сумм

может принимать лишь значения 0 или 1. Поэтому сумма может принимать значения 0, 1, -1.

Целевую функцию рассмотрим в виде

.

Очевидно, что может лишь принимать значения 0 или 1.

Нулевые минимальные значения нелинейных целевых функций ,идостигаются для изоморфных графов и только для них.