
Лекция 10. Непрерывность функции
.pdf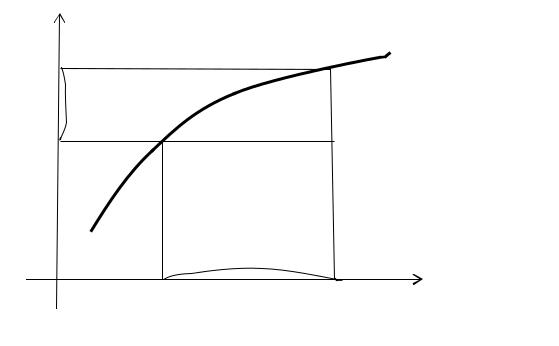
1
Лекция 10. Непрерывность функции в точке и на промежутке
10.1.Непрерывность функции в точке
Пусть |
функция |
определена |
в некоторой точке |
и |
в |
некоторой окрестности этой точки, причем, |
, |
|
|
||
Если |
получит |
некоторое положительное или отрицательное |
- |
||
приращение |
и примет значение |
, то и заданная функция |
|||
получит некоторое приращение |
(рис. 10.1). |
|
|
||
y |
|
|
|
|
|
|
|
M |
|
|
|
y0+∆y |
|
|
|
|
|
|
∆y |
|
|
|
|
y0 |
M0 |
|
N |
|
|
|
|
|
|
||
|
|
∆x |
|
O |
x0 |
x0+∆x |
x |
|
|||
|
|
|
Рис. 10.1 |
Определение 1. Функция |
называется непрерывной в точке , если |
||
она определена в некоторой окрестности этой точки, включая и саму эту точку и если выполняется равенство
lim y 0
x 0
Можно доказать, что определение непрерывности функции,
сформулированное в предыдущей лекции эквивалентно определению 1 этой лекции. Действительно, функция f(x) непрерывна в точке x0, если выполняется равенство
2 |
|
lim f (x) f (x0 ) |
, |
x x0 |
где x=x0+∆x. Если x→x0, то ∆x= x-x0→0. Следовательно, равенство можно записать в виде
lim f (x |
x) f (x ) |
|
|
x 0 |
0 |
0 . |
|
По теореме 1 лекции |
2 |
из последнего равенства следует, что |
|
, где |
lim (x) 0 |
. Откуда получаем, что |
|
|
|
x 0 |
|
|
|
, то есть, lim y 0 . Таким образом, из |
|
|
|
x 0 |
|
определения лекции 2 следует данное выше определение 1. Можно доказать и обратное.
Пример 1. Доказать, что функция y=sinx непрерывна в любой точке x0.
Решение. Дадим x0 приращение ∆x, получим новую точку x=x0+∆x, тогда заданная функция получит приращение
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
x |
|
x |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
lim y lim |
2sin |
|
cos x |
|
|
2sin 0 cos(x 0) |
2 0 cos x 0. |
|||||||||
|
|
|||||||||||||||
x 0 |
x 0 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|||
Аналогичным образом рассматривая все основные элементарные функции,
можно доказать теорему 4 из лекции 3.
10.2.Свойства функций непрерывных в точке
Свойство 1. Если функции f(x) и g(x) непрерывны в точке x0, то их сумма f(x)±g(x), произведение f(x)g(x) и частное f(x)/g(x) (при условии, что g(x0)
отлична от нуля), являются функциями непрерывными.
3
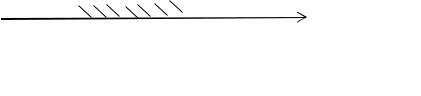
Пусть приращение ∆x>0, тогда промежуток (x0-∆x, x0+∆x) является окрестностью точки x0 (рис. 10.2).
0 |
x0 |
0 |
x |
x0-∆x |
x0+∆x |
Рис. 10.2.
Свойство 2. Если функция f(x) непрерывна в точке x0 и положительна в ней f(x0) >0 , то существует такая окрестность (x0-∆x, x0+∆x) точки x0, что функция положительна f(x) >0 во всей этой окрестности, то есть при xϵ(x0-∆x, x0+∆x).
Свойство 3. Если функция y=f(u) непрерывна в точке u0, а функция u=ϕ(x)
непрерывна в точке x0, такой что u0=ϕ(x0), то сложная функция y=f(ϕ(x))
непрерывна в точке x0.
10.3.Задача о непрерывном начислении процентов
Задача. Первоначальный вклад в банк составил Q0 денежных единиц. Банк ежегодно начисляет p% годовых. Необходимо найти размер вклада Qt через t лет.
Через 1 год размер вклада будет равен Q1= Q0+ Q0 p/100= Q0(1+ p/100).
Через 2 года размер вклада будет равен Q2= Q1+ Q1 p/100= Q1(1+ p/100),
подставив выражение для Q1, получаем: Q2= Q0(1+ p/100)2.
Через 3 года размер вклада будет равен Q3= Q2+ Q2 p/100= Q2(1+ p/100),
подставив выражение для Q2, получаем: Q3= Q0(1+ p/100)3.
Через t лет размер вклада будет равен выражению Qt= Q0(1+ p/100)t.
Если начислять проценты по вкладам не один раз в год, а n раз, то при том же ежегодном приросте в p% начисления за 1/n часть года p/n
процентов, а размер вклада за t лет при nt начислениях составит:
Q Q |
|
|
|
p nt |
||
1 |
|
|
|
|||
|
|
|||||
t |
0 |
|
|
100n . |
||
4
Будем предполагать, что проценты по вкладам начисляются каждое полугодие, тогда n=2, ежеквартально - n=4, ежемесячно - n=12, ежедневно - n=365, ежечасно - n=365ˑ24 и так далее, непрерывно n→∞. Размер вклада за t лет при непрерывном начислении процентов можно найти как предел
|
|
|
|
|
p |
nt |
Qt |
lim Q0 |
1 |
|
|
|
|
|
|
|||||
|
n |
|
|
100n . |
||
|
|
|
|
|
|
|
|
Если |
|
вместо |
n подставить бесконечность, то получим |
||
неопределенность вида 1∞, следовательно, необходимо применить второй
|
|
|
|
|
|
|
|
|
|
1 n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
lim 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
замечательный предел |
n |
|
|
n |
|
. Для этого предел запишем в виде |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
tp |
|
|
|
|
|
|
|
|
|
|
|
tp |
|
|
|
||
|
|
|
|
|
|
|
|
100n |
|
|
|
|
|
|
|
|
|
|
|
|
100n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
100 |
|
tp |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
p |
|
|
p |
|
|
|
|
|
|
|
|
p |
|
p |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Qt |
Q0 lim |
1 |
|
|
|
|
|
|
|
|
|
Q0 lim 1 |
|
|
|
|
|
|
|
Q0e100 |
||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
n |
|
|
100n |
|
|
|
|
|
|
|
n |
|
100n |
|
|
|
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
10.4.Точки разрыва и их классификация
Определение 2. Точка x0 называется точкой разрыва функции f(x), если в ней нарушается хотя бы одно из условий непрерывности, то есть, если функция не определена в точке x0, или не существует предела функции f(x)
при x→x0, или предел при x→x0 не равен значению функции
lim f (x) f (x0 ) |
|
x x0 |
. |
|
Определение 3. Точка x0 называется точкой разрыва первого рода функции f(x), если существуют оба конечных односторонних предела функции слева,
если x→x0-0 и справа, если x→x0+0 не равные друг другу
lim f (x) lim f (x) |
|
||
x x0 0 |
x x0 |
0 |
. |
|
|
|
|
Определение 4. Точка x0 |
называется |
точкой разрыва второго рода |
|
функции f(x), если хотя бы один из односторонних пределов функции слева,
если x→x0-0 и справа, если x→x0+0 равен бесконечности или не существует.
5
Определение 5. Точка x0 называется точкой устранимого разрыва функции f(x), если существует конечный предел этой функции при условии, что x→x0,
но он не равен значению функции в этой точке
lim f (x) f (x0 ) |
. |
|
|
|
|
|
x x0 |
|
|
|
|
||
|
|
|
|
|
||
|
|
y |
x2 |
9 |
|
|
Пример 2. Исследовать на непрерывность функцию |
x |
3 . В случае |
||||
|
||||||
разрыва определить тип точки разрыва.
Решение. Функция элементарна, следовательно, непрерывна во всей своей
|
x ( ;3) (3; ) |
области определения, то есть, в промежутке |
. |
В точке x=3 функция терпит разрыв, так как она в этой точке не определена.
Определим тип разрыва, для этого вычисляем предел функции при условии,
|
|
|
|
lim |
x2 |
9 |
|
0 |
lim |
(x 3)(x 3) |
lim(x 3) 6 |
|
||||||
что x→3-0 |
|
|
|
|
|
|
|
, |
||||||||||
|
x |
3 |
0 |
|
x 3 |
|||||||||||||
|
|
|
x 3 0 |
|
|
x 3 0 |
|
|
x 3 |
|
||||||||
и при условии, что x→3+0 |
|
|
|
|
|
|
|
|||||||||||
lim |
x2 |
9 |
|
|
0 |
|
lim |
|
(x 3)(x 3) |
lim(x 3) |
6 |
|
||||||
x |
|
|
|
|
|
|
|
x 3 |
|
|
||||||||
x 3 0 |
3 0 |
|
x 3 0 |
|
|
x 3 |
|
|
|
|||||||||
Как видим, оба односторонних предела существуют, это означает, что и обычный предел существует и конечен, следовательно, точка x=3 является точкой устранимого разрыва функции. Заданную функцию можно доопределить до непрерывной функции. Введем функцию
|
2 |
9 |
|
|
|
|
|
x |
|
, |
если |
x 3, |
|
f (x) x 3 |
||||||
|
|
6, |
|
если |
x 3. |
|
|
|
|
||||
Эта функция является непрерывной при любых значениях независимой переменной, так как выполняются все условия непрерывности, так как
lim f (x) f (3) 6.
x 3
Поэтому и название точки устранимого разрыва.
6
|
1 |
|
|
|
y e |
|
|
|
1 x |
||
Пример 3. Исследовать на непрерывность функцию |
|
|
. В случае |
разрыва определить тип точки разрыва. |
|
|
|
Решение. Функция элементарна, следовательно, непрерывна во всей своей
|
x ( ;1) (1; ) |
области определения, то есть, в промежутке |
. |
В точке x=1 функция терпит разрыв, так как она в этой точке не определена. Определим тип разрыва, для этого вычисляем предел функции
при условии, что x→1-0
1 |
|
|
1 |
|
|
|||
lim e |
|
|
|
| x 1 1 x 0 | e |
|
|
|
e , |
1 x |
0 |
|||||||
x1 0 |
|
|
|
|
||||
и при условии, что x→1+0 |
|
|
|
|
||||
1 |
|
|
1 |
|
|
|||
lim e |
|
| x 1 1 x 0 | e |
|
e 0 . |
||||
1 x |
0 |
|||||||
x1 0 |
|
|
|
|
||||
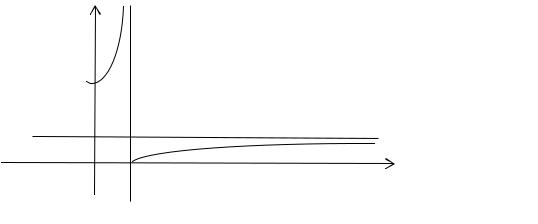
Как видим, предел слева равен ∞, следовательно, x=1 точка разрыва второго рода. Геометрически это означает, что график заданной функции имеет вертикальную асимптоту. График функции вблизи точки разрыва изображен на рисунке 10.3.
y
e
1
0
o 1
x
Рис. 10.3
Пример 4. Исследовать на непрерывность функцию
sin x, |
если |
x 0, |
|
|
|
x, |
если |
0 x 1, |
|
f (x) |
|
|||
|
|
если |
x 1. |
. |
x 1, |
|
|||
7
В случае разрыва определить тип точки разрыва.
Решение. Функция не является элементарной. Она элементарна на каждом из промежутков (-∞;0), (0;1) и (1;+∞). Следовательно, непрерывна в каждом из этих промежутков. Исследуем каждую из точек x=0 и x=1 на непрерывность.
Точка x=0. |
|
|
|
|
1. |
f(0)=0. |
|
|
|
2. |
lim |
f (x) | x 0 | |
lim sin x 0. |
|
|
x 0 0 |
|
x 0 0 |
|
|
lim |
f (x) | x 0 | |
lim x 0. |
Пределы справа и слева равны, |
|
x 0 0 |
|
x 0 0 |
|
следовательно, существует предел функции lim f (x) 0.
x 0
3. lim f (x) f (0).
x 0
Все условия непрерывности выполнены, следовательно, в точке x=0
функция непрерывна. |
|
|
|
|
|
|
||
Точка x=1. |
|
|
|
|
|
|
|
|
1. |
f(1)=1. |
|
|
|
|
|
|
|
2. |
lim |
f (x) | x 1| lim x 1. |
|
|
|
|||
|
x 1 0 |
|
x 1 |
|
|
|
||
|
lim |
f (x) | x 1| lim(x 1) 2. |
Пределы справа и слева |
|||||
|
x 1 0 |
|
x 1 |
|
|
|
||
|
существуют, конечны и не равны друг другу, следовательно, в точке x=1 |
|||||||
|
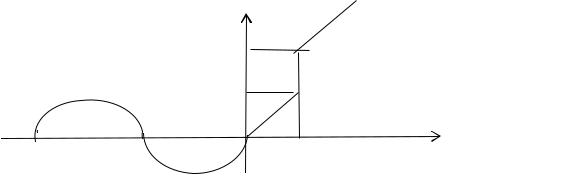
функция терпит разрыв первого рода. График функции изображен на |
|||||||
|
рисунке 10. 4. |
|
y |
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
2 |
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
1 |
x |
Рис. 10.4. |
|
|
|
|
|
|
|
|||
8
10.5.Свойства функций непрерывных на отрезке
Определение 6. Функция y=f(x) непрерывна на промежутке X, если она непрерывна в каждой точке этого промежутка.
Свойство 1. Если функция y=f(x) непрерывна на отрезке [a;b], то она ограничена на этом отрезке.
Свойство 2. Если функция y=f(x) непрерывна на отрезке [a;b], то она достигает на этом отрезке наименьшего значения m и наибольшего значения
M.
Свойство 3. Если функция y=f(x) непрерывна на отрезке [a;b] и значения ее на концах отрезка f(a) и f(b) имеют противоположные знаки, то внутри отрезка существует, по крайней мере, одна точка cϵ(a;b), такая что f(с)=0.
