Лекция 9. Вычисление пределов
.pdf1
Лекция 9. Свойства пределов и их вычисление
9.1.Основные теоремы о пределах
Не будем писать ни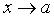 
, ни 
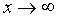, подразумевая то или другое.
Теорема 1. Функция не может иметь более одного предела.
Доказательство. Пусть функция |
|
имеет два предела |
и |
|||
, причем, |
. Тогда по свойству 1 |
бесконечно малых будем |
||||
иметь, что |
, где |
и |
, |
где |
. Вычитая эти |
|
равенства одно из другого, получим: |
|
|
|
, откуда |
|
|
. Это равенство невозможно, так как по свойству 2 бесконечно малых
величина является бесконечно малой, а . Следовательно,
наше предположение о существовании двух разных пределов неверно.
Теорема 2. Предел алгебраической суммы двух, трех и вообще конечного числа функций равен алгебраической сумме пределов этих функций:
.
Теорема 3. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций.
.
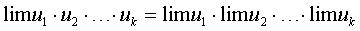Следствие. Постоянный множитель можно выносить за знак предела.
Действительно, если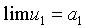 
, - постоянная величина и, следовательно,
, то
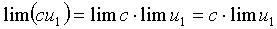, что и требовалось доказать.
2
Теорема 4. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля:
, если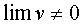 
.
Пример 1.Найти lim(5x2 6x 7) .
x 1
Решение. Из приведенных выше теорем следует, что
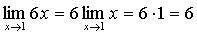и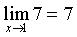 
Пример 2. Найти lim |
|
x2 1 |
|
. |
|
2x |
2 |
x 1 |
|||
x 0 |
|
|
|||
Решение. Из приведенных выше теорем следует, что
; 
;
.
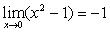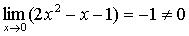5.2.Непрерывность функций
Определение. Функция |
называется непрерывной в точке , если она |
удовлетворяет следующим трем условиям: |
|
1. Она определена в точке |
; |
3
2. Имеет конечный предел при ;
3. |
lim f (x) f (x0 ) . |
|
|
|
|
x x0 |
|
|
|
Пример 3. Функция |
|
. Не является непрерывной в точке |
, так как |
|
|
||||
она в этой точке не определена.
Определение непрерывности может быть записано в символическом
виде
lim f (x) f (lim x) . |
|
x x0 |
x x0 |
То есть, для непрерывной функции возможна перестановка знаков предела и функции.
Теорема 5. Всякая элементарная функция непрерывна во всей своей области определения.
Таким образом, вычисление пределов элементарных функций сводится к простой подстановке предельного значения аргумента в
выражение функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 4. Найти предел функции |
√ |
|
|
√ |
при |
||||
. |
|
|
|
|
|
|
|
|
|
Решение. |
Так |
как |
функция |
|
|
элементарна, |
то |
||
|
|
|
|
|
|||||
lim (t) (6) 6 |
36 20 lg( 6 |
36 20) 24 lg10 24 1 23 |
|||||||
t 6 |
|
|
|
|
|
|
|
|
|
И в этом примере предел вычислен сразу. Однако чаще встречаются
случаи, когда для вычисления примера необходимо применять специальные
методы.
4
5.3.Методы раскрытия неопределенностей
5.3.1. Неопределенность вида
Пример 5. Найти lim |
|
|
x2 1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
x |
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Решение. Если вместо переменной x подставить |
, то в числителе и в |
|||||||||||||||||||||||||||||||||||||||||
знаменателе получится |
|
, то есть, будем иметь неопределенность |
|
|
|
. |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Числитель и знаменатель делим на выражение |
, |
|
где |
|
максимальная |
|||||||||||||||||||||||||||||||||||||
степень числителя и знаменателя. В данном примере |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x2 |
|
|
1 |
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|||||||||
|
x2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
x3 |
x3 |
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
lim |
lim |
|
|
|
|
|
|
|
lim |
|
|
x |
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x 2x3 x 1 |
x 2x3 |
|
x |
1 |
|
x |
|
1 1 |
|
|
1 1 |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
x3 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
x3 |
x3 |
|
x3 |
|
|
|
|
|
|
|||||||||||||||||||||||||||
По теореме о связи бесконечно малых и бесконечно больших, изложенной в
лекции 8, имеем: |
|
|
и |
|
|
|
|
|
. Тогда окончательно |
||||
|
|
|
|
|
|
|
|||||||
lim |
x2 |
1 |
|
|
|
0 0 |
|
|
|
|
0 |
0. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 0 |
|
|
|
|
|||||
x 2x3 x 1 |
|
|
0 2 |
|
|||||||||
5.3.2. Неопределенность вида
А). Под пределом стоит отношение двух многочленов
В этом случае, многочлены необходимо разложить на простые множители и сократить на выражение , где предельное значение аргумента .
x2 1 Пример 6. . Найти lim 2x2 x 1.
x 1
5
Решение. Если вместо переменной x подставить 1, то в числителе и в знаменателе получится 0, то есть, будем иметь неопределенность .
Раскладываем числитель и знаменатель на простые множители:
lim |
x2 1 |
. lim |
(x 1)(x 1) |
. |
|||||||
2x2 x 1 |
|
|
|
|
|
|
1 |
|
|||
x 1 |
x 1 |
2(x 1)(x |
) |
|
|||||||
|
|
|
2 |
|
|||||||
Сократив на скобку |
|
|
, окончательно имеем: |
||||||||
|
|
||||||||||
lim |
x2 1 |
. lim |
(x 1) |
|
2 |
. |
|
|
|
||
2x2 x 1 |
2x 1 |
3 |
|
|
|
||||||
x 1 |
x 1 |
|
|
|
|
|
|||||
Б). Под пределом стоит функция, содержащая иррациональное выражение
1. Метод введения новой переменной
Выражение, стоящее под корнем обозначают через выражение |
, где |
выбирают таким, чтобы все корни извлеклись нацело. После |
этого |
получаем предел как в пункте А.
x 1
Пример 7. Найти limx 1 3 x 1.
Решение. Если вместо переменной x подставить 1, то в числителе и в
знаменателе получится 0, то есть, будем иметь неопределенность |
|
. Вводим |
|||||||
|
|||||||||
|
|
|
|
|
|
√ |
|
|
|
новую переменную |
. Как видим, если |
, то |
и √ |
, |
|||||
√√ . Тогда в новых переменных предел принимает вид:
|
|
|
|
|
|
t3 |
|
|
|
(t 1)(t 2 t |
|
|
t 2 |
|
|
|
|
|
|
|
|
lim |
|
x 1 |
. lim |
1 |
lim |
1) |
lim |
t 1 |
|
1 1 1 |
1,5 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
t 2 |
1 |
(t 1)(t 1) |
|
|
t 1 |
|
|
1 |
|||||||||
3 |
x 1 |
|
|
1 |
|||||||||||||||||
x 1 |
t 1 |
t 1 |
|
t 1 |
|
|
|
||||||||||||||
6
2.Перевод иррациональности из знаменателя в числитель, а из числителя в знаменатель
Используя формулы сокращенного умножения
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
решим предыдущий пример. |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 8. Найти lim |
|
|
|
x |
1 |
. |
|
|
|
|
|
|
|
|
|||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|||
Решение. Числитель и знаменатель |
|
умножаем на выражение √ |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
x 1 |
. lim |
( |
x 1)( |
x 1)(3 |
x2 |
|
3 |
x 1) |
. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x 1 3 |
|
|
x 1 ( |
x 1)(3 |
x 1)(3 |
x2 |
|
3 |
x 1) |
|
|||||||||||||||
Учитываем, что
(√ |
|
|
|
|
)(√ |
|
|
) |
|
|
и (√ |
|
|
|
)(√ |
|
|
|
√ |
|
) |
|
|
|
. Получаем: |
|||||||||||||
|
|
|
|
|
|
|
x 1 3 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
x2 3 |
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
lim |
|
|
x 1 |
lim |
x |
lim |
3 |
|
3 x |
1 |
|
1 1 1 |
1,5 . |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
3 x 1 |
|
|
x 1 x 1 |
|
|
|
|
|
x 1 |
|
1 1 |
||||||||||||||||||||||||||
x 1 |
|
|
|
x 1 |
|
x 1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
В). Под пределом стоит выражение, содержащее тригонометрические
функции
Такие пределы вычисляются с помощью первого замечательного
предела lim |
sin |
lim |
|
1. |
||||
|
|
|
|
|||||
0 |
0 sin |
|
||||||
Пример 9. . Найти lim |
1 cos x |
. |
||||||
|
|
|
|
|
||||
|
|
x |
2 |
|
||||
|
|
x 0 |
|
|
|
|
|
|
7
Решение. Если вместо переменной x подставить 0, то (учтем, что числителе и в знаменателе получится 0, то есть, будем неопределенность . Применим формулу тригонометрии
|
|
|
|
|
2 |
x |
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
|
x |
|
x |
|
|
|||
|
1 cos x |
|
2 sin |
|
|
|
|
2 sin |
|
sin |
|
|
|
1 |
lim |
sin |
|
|
lim |
sin |
|
|
|
||||||
lim |
lim |
|
2 |
|
lim |
2 |
2 |
|
|
2 |
2 |
|
|
||||||||||||||||
|
x2 |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x 0 |
|
x 0 |
|
|
x 0 |
|
x x |
4 |
|
|
|
2 x 0 |
x |
|
|
x 0 |
x |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
||||
) в
иметь
.
1
2 .
5.3.3. Неопределенность вида
Для раскрытия этой неопределенности надо выполнить
алгебраические преобразования и свести ее к неопределенности |
|
или |
|
. |
|
|
|||||||
|
|
||||||||||||
Пример 10. Вычислить предел lim(8x ctgx) . |
|
|
|
|
|
|
|
|
|
|
|||
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
Решение. Если вместо переменной x подставить 0, то (учтем, что |
) |
||||||||||||
будем иметь неопределенность |
. Запишем выражение, |
стоящее под |
|||||||||||
пределом в |
виде дроби |
lim(8x ctgx) lim |
8x cos x |
. |
Если |
вместо |
|||||||
|
|||||||||||||
|
|
x 0 |
x 0 |
sin x |
|
|
|
|
|
|
|
|
|
переменной x |
подставить 0, |
то |
будем иметь |
неопределенность |
|
|
|
|
и |
||||
|
|
|
|
||||||||||
выражение, стоящее под пределом содержит тригонометрические функции,
следовательно, необходимо применить первый замечательный предел
lim |
sin |
1. Окончательно lim(8x ctgx) lim 8 cos x lim |
x |
8 1 1 8 . |
|||
|
sin x |
||||||
x 0 |
x 0 |
x 0 |
x 0 |
|
|||
5.3.4. Неопределенность вида
Для |
раскрытия |
этой |
неопределенности |
надо |
|
выполнить |
||
алгебраические преобразования и свести ее к неопределенности |
|
или |
|
. |
||||
|
|
|||||||
8
|
|
|
|
|
|
|
|
|
lim |
|
1 |
|
|
|
|
|
|
2 |
|
. |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Пример 11. . Найти |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x 1 x 1 |
|
|
|
x |
2 1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Решение. Если вместо переменной x |
подставить 1, то (учтем, что |
|
|
|
|
) |
||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||
будем иметь неопределенность |
|
|
|
|
|
|
|
|
. Приведем выражение, стоящее под |
|||||||||||||||||||||||||||
пределом к общему знаменателю. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
1 |
|
|
|
2 |
|
|
lim |
|
|
x 1 2 |
lim |
|
x 1 |
lim |
1 |
|
|
|
1 |
|
|||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
x 1 x 1 |
|
x2 1 |
|
x 1 |
|
(x 1)(x 1) |
x 1 |
|
(x 1)(x 1) |
x 1 |
x 1 |
|
2 |
|
||||||||||||||||||||||
|
|
|
|
|
5.3.5. Неопределенность вида . |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
Такие |
пределы вычисляются |
с |
помощью второго |
замечательного |
|||||||||||||||||||||||||||||||
|
|
|
lim 1 lim 1 1 |
|
n |
1. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
предела |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
0 |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Пример 12. . Найти lim 1 5x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Если вместо переменной x |
подставить 0, то (учтем, что |
|
|
|
) |
|||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||
будем |
|
иметь |
неопределенность |
. |
Следовательно, необходимо |
|||||||||||||||||||||||||||||||
использовать второй замечательный предел. Введем новую переменную
, тогда если |
|
, то и |
, при этом |
|
|
|
. В новых переменных |
|||||||||||
|
|
|
|
|||||||||||||||
предел принимает вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3 |
|
3 ( 5) |
|
|
1 |
15 |
|
|
|
|
1 |
15 |
|
15 |
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||||
lim 1 5x x |
lim 1 |
|
|
|
|
|
|
e |
. |
|||||||||
|
lim |
1 |
lim 1 |
|
|
|||||||||||||
x 0 |
0 |
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|||