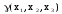Двойственные функции
опр
|| функция
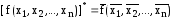 называется двойственной функцией к
функции
называется двойственной функцией к
функции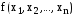 .
.
Пример.
|
x1 |
x2 |
x3 |
|
|
|
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
0 |
Правило ||
Чтобы
получить двойственную функцию нужно
инвертировать
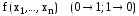 ,
а затем перевернуть таблицу.
,
а затем перевернуть таблицу.
Соответствие элементарных функций
f
0, 1, x,
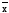 ,x1&
,x1&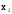 ,x1Ú
,x1Ú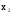
f*
1, 0, x,
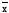 ,x1Ú
,x1Ú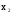 ,
x1&
,
x1&
Из определения двойственности следует, что
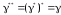
Теорема || Пусть
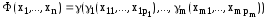
Тогда
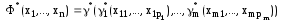
Доказательство ||
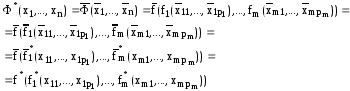
Отсюда вытекает принцип двойственности: двойственной к формуле
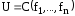 является формула
является формула
 .
.
Пусть
формула содержит только символы &, Ú,
Ø.
Тогда для получения
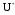 изU
нужно заменить:
изU
нужно заменить:

Из принципа двойственности вытекает, что
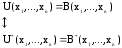 .
.
В частности,
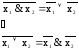 .
.
Совершенная дизъюнктивная нормальная форма
Совершенная дизъюнктивная нормальная форма.
Обозначим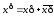 ,
гдеd
равен либо 0, либо 1. Тогда
,
гдеd
равен либо 0, либо 1. Тогда
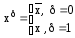 .
.
Поскольку
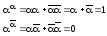 ,
,
то xd=1 Û x=d.
Теорема
о разложении функции по переменным ||
Каждую функцию Булевой алгебры
 при любом
при любом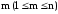 можно
представить в следующей форме:
можно
представить в следующей форме:

 ,
,
где
дизъюнкция берется по всем наборам
значений переменных
 .
||
.
||
опр || Это представление называется разложением функции по m переменным x1,…xm.||
Доказательство.
Рассмотрим произвольный набор значений
 .
Левая часть равенства имеет вид
.
Левая часть равенства имеет вид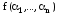 .
Правая часть
.
Правая часть

(в
сумме только одно произведение отлично
от нуля: то в котором
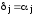 )
)
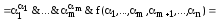
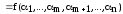 .
.
Теорема доказана.
Разложение по одной переменной
1)
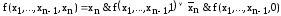
Разложение по всем n переменным
2)
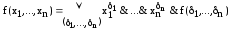
При
Опр. Это разложение называется совершенной дизъюнктивной нормальной формой представления функции f(x1,…,xn).
Совершенная конъюнктивная нормальная форма
Пусть
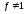 .
Согласно
теореме двойственности
.
Согласно
теореме двойственности
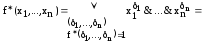

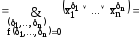
Это разложение называется совершенной конъюнктивной нормальной формой.
Примеры
1)
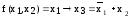
2)
|
x1 |
x2 |
f |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
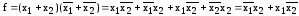
3)
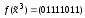
|
x1 |
x2 |
x3 |
f |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
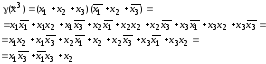
4)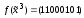
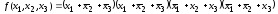

|
x1 |
x2 |
x3 |
x4 |
|
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
1 |
|
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
0 |
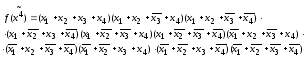
5)
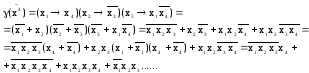
Полнота множеств

Замкнутость множеств
Опр
|| система функций
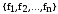 изP2
(множества всех булевых функций)
называется функционально полной, если
любая булева функция может быть записана
в виде формулы через функции этой
системы.
изP2
(множества всех булевых функций)
называется функционально полной, если
любая булева функция может быть записана
в виде формулы через функции этой
системы.
Пример:
1) Само множество
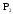 ;
;
2) ;
;
3)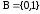 - не полна.
- не полна.
Теорема
|| Пусть даны две системы функций из
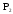
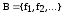 ,
(I)
,
(I)
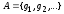 .
(II)
.
(II)
Известно, что система I полная и каждая функция системы I выражается через функции системы II. Тогда система II является полной.
Доказательство
|| Пусть
 .
В силу полноты сист.I
функцию h
можно выразить в виде формулы
.
В силу полноты сист.I
функцию h
можно выразить в виде формулы
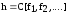 .
По условию теоремы
.
По условию теоремы
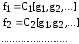
Поэтому
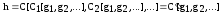 ч. и т.д.
ч. и т.д.
Примеры ||
1)
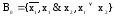 - полная.
- полная.
2)
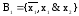 - тоже полная, так как
- тоже полная, так как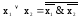 .
.
3)
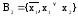 - тоже полная.
- тоже полная.
4)
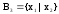 - тоже полная, так как
- тоже полная, так как
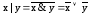 ,
,
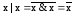 ,
,
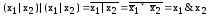 .
((2) – I)
.
((2) – I)
5)
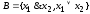 - неполная. Докажем это от противного.
- неполная. Докажем это от противного.
Предположим,
что
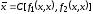 .
.
Но
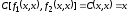 .
Противоречие.
.
Противоречие.
6)
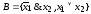 - неполная (сохраняет константу 0 – см.
след лекц.).
- неполная (сохраняет константу 0 – см.
след лекц.).
7)
 - неполная (сохраняет константу 1 – см.
след лекц.).
- неполная (сохраняет константу 1 – см.
след лекц.).
6’)
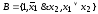 - полная
- полная
8)


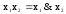 тогда взяв в
качестве сист. I
сист. 2) можно заключить, сист. функций
8) – полная. Тем самым, справедлива
тогда взяв в
качестве сист. I
сист. 2) можно заключить, сист. функций
8) – полная. Тем самым, справедлива
Теорема
Жегалкина || Каждая функция из
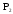 может быть выражена при помощи полинома
по модулю 2 – (полинома Жегалкина):
может быть выражена при помощи полинома
по модулю 2 – (полинома Жегалкина):
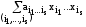 .
.
Имеем:
число разных сочетаний
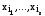 равно числу подмн-в мн-ва изn
элементов. Каждое aik
может принимать одно из 2-х значений
{0,1}. Тогда число разных пол. Жег. равно
равно числу подмн-в мн-ва изn
элементов. Каждое aik
может принимать одно из 2-х значений
{0,1}. Тогда число разных пол. Жег. равно
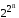 ,
т.е. равно числу различных булевых
функций.
,
т.е. равно числу различных булевых
функций.
Т. о. получаем единственность представления функций через пол. Жег.
Примеры
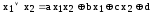
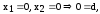

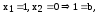
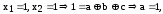
Следовательно,
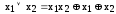
Пока опустим
2 способ T-преобразов. вектора функции
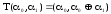
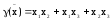
|
X1 |
x2 |
x3 |
|
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
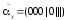

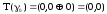
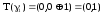
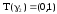

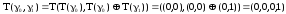
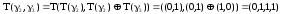


3 способ – алгебраических преобразований
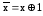
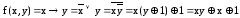
Опр. Пусть M – некоторое подмножество функций из P2. Замыканием M называется мн-во всех булевых функций, представимых в виде формул через функции мн-ва M. Обозначается [M].
Замечание. Замыкание инвариантно относ. операций введения и удаления фиктивных перем.
Примеры.
1) M=P2, [M]=P2.
2) M={1,x1Åx2}, [M] – мн-во L всех линейных ф-й вида
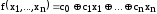 ,
(ciÎ{0,1}).
,
(ciÎ{0,1}).
Свойства замыкания:
[M]=M;
[[M]]=[M];
M1ÍM2 Þ [M1]Í[M2];
[M1ÈM2]Ê[M1]È[M1].
Опр. Класс (мн-во) M называется (функционально) замкнутым, если [M]=M.
Примеры.
Класс M=P2 функционально замкнут;
Класс {1,x1Åx2} не замкнут;
Класс L замкнут (линейное выражение, составленное из линейных выражений линейно).
Новое определение полноты. M – полная система, если [M]=P2.
Замкнутые классы
1)
Обозначим через
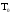 - класс всех булевых функций
- класс всех булевых функций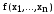 ,
сохраняющих константу 0, т.е. функций,
для которых выполняется равенство
,
сохраняющих константу 0, т.е. функций,
для которых выполняется равенство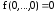 .
.
При добавлении несущественной переменной равенство не меняется.
Функции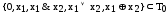 ,
,
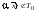 .
.
Количество
таких функций
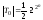 (n
– число переменных) т.к. в первой строке
всегда содержит 0. (У второй половины
1).
(n
– число переменных) т.к. в первой строке
всегда содержит 0. (У второй половины
1).
T0 – замкнутый класс, т.к. если
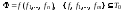 ,
то
,
то
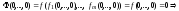
 .
.
2)
Обозначим через
 - класс всех булевых функций
- класс всех булевых функций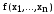 ,
сохраняющих константу 1, т.е. функций,
для которых выполняется равенство
,
сохраняющих константу 1, т.е. функций,
для которых выполняется равенство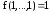 .
.
Класс вместе с любой функцией содержит равную ей функцию.
Функции
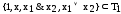 ,
,
 .
.
Класс
 состоит из функций двойственных классу
состоит из функций двойственных классу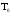 (следует из определения).
(следует из определения).
Поэтому
все свойства класса
 переносятся на класс
переносятся на класс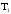 .
.
 .
.
3)
S
– класс – класс всех самодвойственных
функций, т.е.
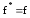 .
.
Функции
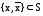 ,
,
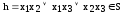 ,
т.к.
,
т.к.
 Для
самодвойственной функции имеет место
тождество
Для
самодвойственной функции имеет место
тождество
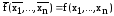 .
.
Тем
самым на наборах
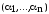 и
и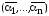 ф-я принимает противоположные значения
(определяется половиной комбинацийxi).
Поэтому число самодвойственных функций
равно
ф-я принимает противоположные значения
(определяется половиной комбинацийxi).
Поэтому число самодвойственных функций
равно
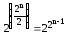 .
.
Докажем, что класс S замкнут.
Пусть
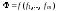 ,
,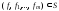 ,
т.е.
,
т.е.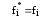 .
Тогда
.
Тогда
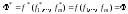 .
.
4. Обозначим
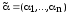 ,
,
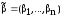 ,
, .
.
опр
|| Для 2х
наборов
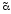 и
и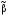 выполнено отношение предшествования
выполнено отношение предшествования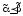 ,
если
,
если .
.
Пример.

Очевидно,
что если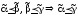 .
.
Таким
образом, множество всех наборов длины
n
по отношению к операции предшествования
 является частично упорядоченным.
является частично упорядоченным.
Опр.
|| функция
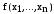 называется монотонной, если для любых
2х
наборов
называется монотонной, если для любых
2х
наборов
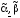 таких, что
таких, что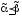 выполняется неравенство
выполняется неравенство
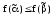 .
.
Монотонные функции:
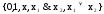 ,
,
 - не монотонны
- не монотонны
Обозначим M – множество всех монотонных функций. Нужно доказать, что этот класс замкнутый.
Пусть
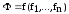 ,
, ,
, .
.
Будем считать, что все fi зависят от x1, xn.
Пусть
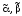 два набора переменных длиныn,
причем
два набора переменных длиныn,
причем
 .
Тогда
.
Тогда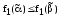 ,
,
………………
 ,
следовательно
,
следовательно
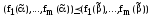 ,
тогда и
,
тогда и
 .
.
Тем
самым
 .
.
5) L – класс всех линейных функций
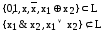
О
замкнутости этого класса мы упоминали
ранее. Кличество линейных функций
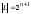 .
.
Эти замкнутые классы не тождественны и они не полны, что следует из таблицы
|
|
T0 |
T1 |
S |
M |
L |
|
0 |
+ |
- |
- |
+ |
+ |
|
1 |
- |
+ |
- |
+ |
+ |
|
|
- |
- |
+ |
- |
+ |
Понятие графа и орграфа
Теория графов
Рассмотрим чертеж вида
города
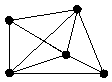
вершины
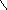

дороги
ребра


Обозначения и определения
V – множество точек – вершины;
X – множество линий – ребра;
Графом называется совокупность множеств вершин и ребер.
v - номер вершины;
{v,w} – обозначение ребра;
{v,v} – петли;
Одинаковые пары - параллельные или кратные ребра;
Кратностью ребер называют количество одинаковых пар.
Пример:
![]() кратность = 3.
кратность = 3.
Если в графе есть петли и/или кратные ребра, то такой граф называют псевдографом.
Псевдограф без петель называется мультиграфом.
Мультиграф в котором ни одна пара не встречается более одного раза называется графом.
Если пары (v,w) являются упорядоченными, граф называется ориентированным (орграфом).
Ребра ориентированного графа называются дугами.
В неориентированном графе ребра обозначаются неупорядоченной парой - {v,w}.
В ориентированном графе дуги обозначаются упорядоченной парой - (v,w).
G, G0 - неориентированный граф, D, D0 – ориентированный.
Обозначают v,w - вершины, x,y,z – дуги и ребра.
Пример
1) V={v1, v2, v3, v4},
X={x1=(v1,v2), x2=(v1,v2), x3=(v2,v2), x4=(v2,v3)}.

изолированная
вершина
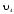
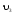
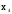
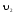
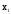

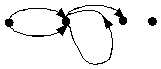
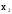
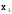
висячая
вершина

2) V={v1, v2, v3, v4, v5},
X={x1={v1,v2}, x2={v2,v3}, x3={v2,v4}, x4={v3,v4}}.

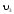
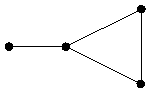

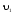
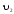
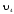
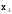
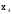


Понятие смежности, инцидентности, степени
опр || Если x={v,w} - ребро, то v и w - концы ребра x.
опр || Если x=(v,w) - дуга орграфа, то v - начало, w – конец дуги.
опр || Если вершина v является концом ребра x неориентированного графа (началом или концом дуги x орграфа), то v и x называются инцидентными.
опр || Вершины v, w называются смежными, если {v,w}ÎX.
опр || Степенью вершины v графа G называется число d(v) ребер графа G, инцидентных вершине v.
опр || Вершина графа, имеющая степень 0 называется изолированной, а степень 1 – висячей
замеч || В неориентированном псевдографе вклад каждой петли инцидентной вершине v в степень вершины v равен 2.
опр || Полустепенью исхода (захода) вершины v орграфа D называется число d+(v) (d-(v)) дуг орграфа D, исходящих из v (заходящих в v).
Замечание || в случае ориентированного псевдографа вклад каждой петли инцидентной вершине v равен 1 как в d+(v), так и в d-(v).
Обозначение: n(G), n(D) количество вершин графа, m(G) - количество ребер, m(D) - количество дуг.
Утверждение. Для каждого псевдографа G выполняется равенство
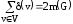 .
.
Для каждого ориентированного псевдографа
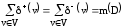
Изоморфизм, гомеоморфизм