
40. Скалярное произведение векторов.
Определение 14.
Скалярным
произведением двух векторов
![]() и
и![]() называетсячисло,
равное произведению длин этих векторов
на косинус угла между ними.
называетсячисло,
равное произведению длин этих векторов
на косинус угла между ними.
Таким образом,
если
![]() ,
,![]() – вектора, то скалярное произведение
обозначается
– вектора, то скалярное произведение
обозначается![]() и
и
![]() .
.
Свойства скалярного произведения.
1) Коммутативность:
![]() .
.
Действительно,
![]() (так как
(так как
![]() ,
то есть четная функция, то
,
то есть четная функция, то![]() )
)![]() .
.
2) Скалярное произведение двух векторов равно длине одного вектора умноженной на проекцию другого на направление первого.
Действительно,
![]() .
.
Отсюда видно, что
если
![]() ,
то
,
то![]() .
.
Следовательно, проекция вектора на ось равна скалярному произведению этого вектора на направляющий вектор оси.
3)
![]() .
.
Действительно,
![]()
![]() .
.
4)
![]() .
.
Действительно,
![]() .
.
5) Для того, что бы два ненулевых вектора были перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение было равно нулю.
![]() Пусть
Пусть
![]()
![]()
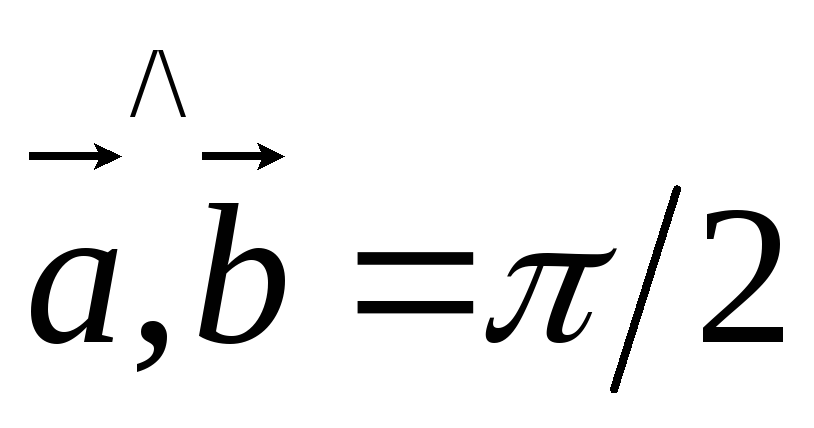
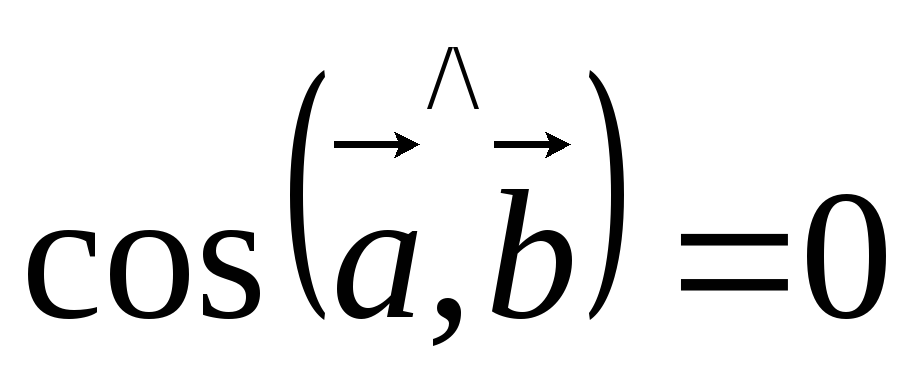
![]() .
.
![]() Пусть
Пусть
![]()
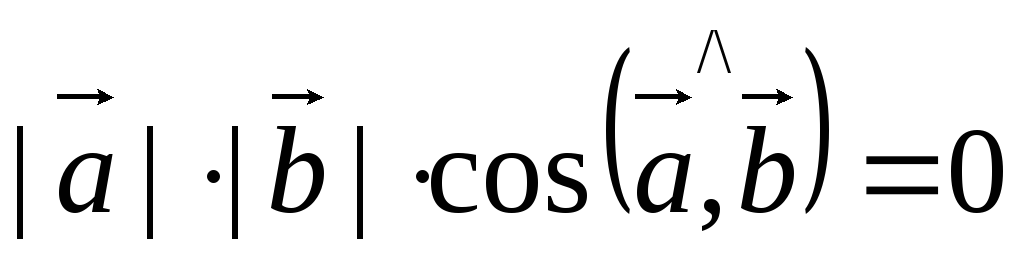 ,
так как
,
так как
![]() ,
,![]()
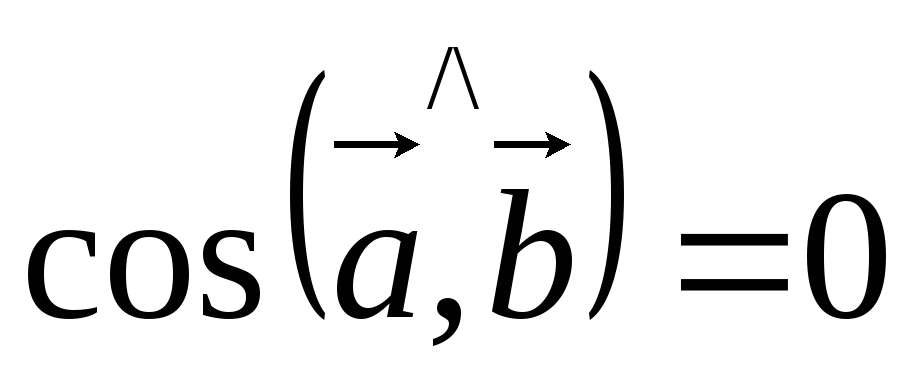
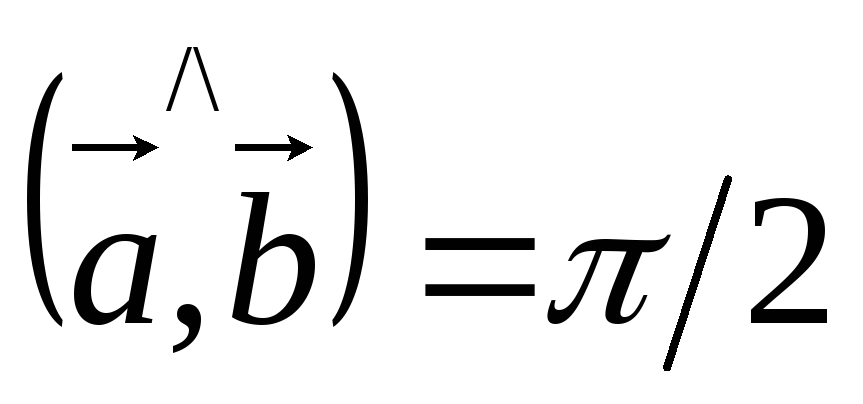
![]()
![]() .
.
6) Пусть
![]()
![]() ,
т.е.
,
т.е.
![]()
скалярный квадрат вектора
скалярный квадрат вектора
![]() равен квадрату длины вектора
равен квадрату длины вектора
![]() .
.
Из последнего
свойства следует, что
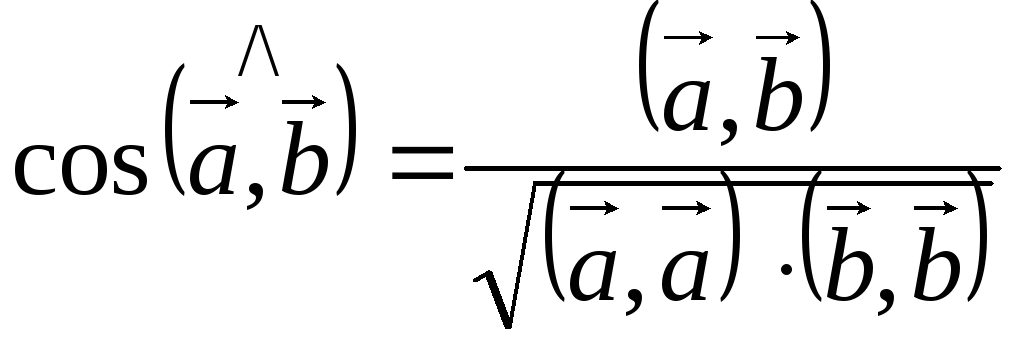 – отдельная строка.
– отдельная строка.
7) Пусть в пространстве
геометрических векторов задан
ортонормированный базис
![]() т.е.
т.е.![]() Тогда
Тогда![]()
Если вектора
![]() заданы своими координатами
заданы своими координатами
![]()
![]() ,
то
,
то
![]()
т.е. в прямоугольной декартовой системе координат скалярное произведение векторов равно сумме произведений соответствующих координат.
Из свойства 7) вытекают некоторые метрические формулы:
1)
![]()
![]()
![]()
2) Если
![]() ,
то
,
то![]() ,
,![]() ,
,![]() .
.
Таким образом, прямоугольные координаты вектора есть его ортогональные проекции на оси прямоугольной системы координат.
Пусть
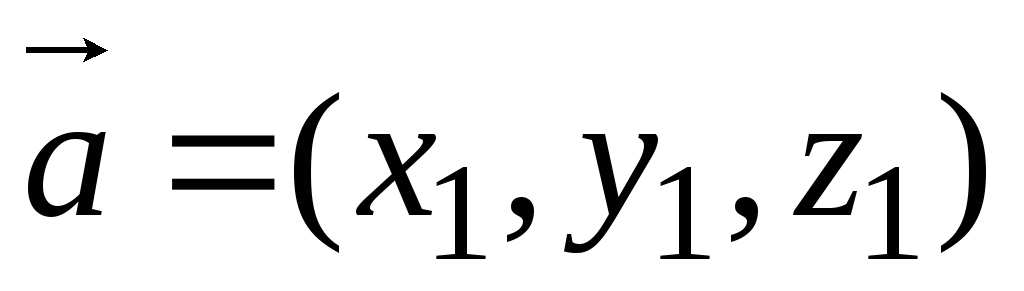 ,
,
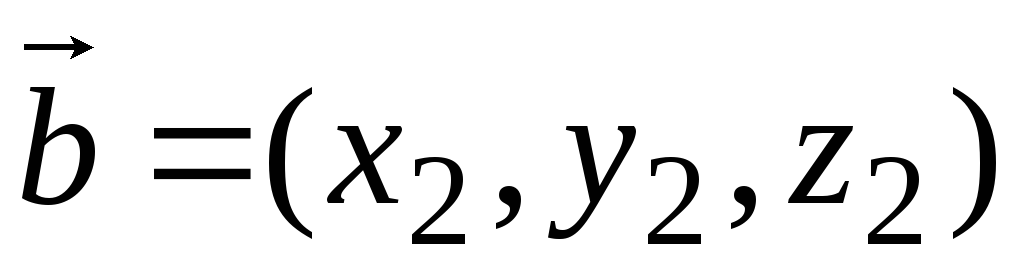
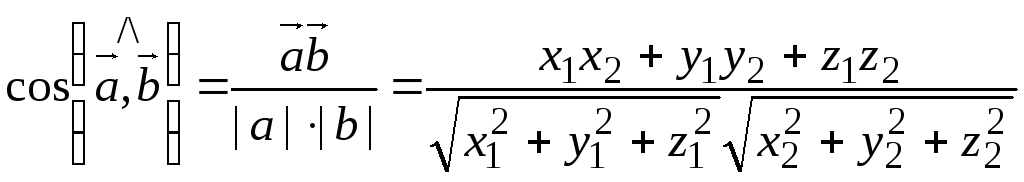 .
.
Таким образом,
![]()
![]()
![]() .
.
Из формулы косинуса
угла между векторами легко найти углы
,
,
,
которые вектор
![]() образует с осями координат. Эти углы
называются направляющими углами.
образует с осями координат. Эти углы
называются направляющими углами.
Имеем:
![]() ,
, ![]() ,
,![]() .
.
![]() ,
,
![]() ,
,![]() называются направляющими косинусами
вектора
называются направляющими косинусами
вектора![]() .
Они связаны соотношением
.
Они связаны соотношением
![]() .
.
Следовательно,
вектор
![]() есть координаты вектора
есть координаты вектора![]() ,
то есть вектора
,
то есть вектора![]() и
и![]() .
.
![]() .
.
5О. Векторное и смешанное произведения векторов.
О пределение
15.Упорядоченная
тройка некомпланарных векторов
пределение
15.Упорядоченная
тройка некомпланарных векторов
![]() называетсяправоориентированной
или просто правой,
если из конца третьего вектора
называетсяправоориентированной
или просто правой,
если из конца третьего вектора
![]() кратчайший поворот от первого
кратчайший поворот от первого![]() ко второму
ко второму![]() виден против часовой стрелки. В противном
случае тройка называетсялевоориентированной
или левой.
виден против часовой стрелки. В противном
случае тройка называетсялевоориентированной
или левой.

Рис. 10. Ориентированные тройки векторов
а) Правая тройка б) Левая тройка
Определение 16.
Векторным
произведением двух векторов
![]() и
и![]() называется вектор
называется вектор![]() ,
удовлетворяющий условиям:
,
удовлетворяющий условиям:
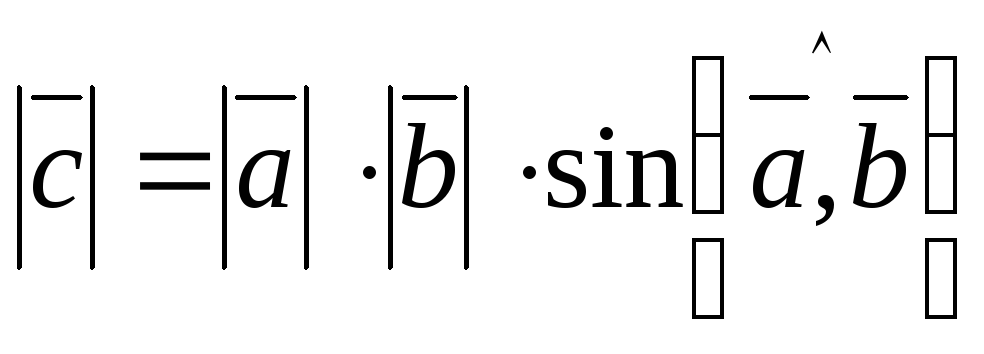 .
.вектор
 ортогонален
векторам
ортогонален
векторам и
и .
.вектора
 образуют правую тройку векторов.
образуют правую тройку векторов.
Обозначение:
![]()
Свойства векторного произведения
Длина вектора
 численно
равна площади параллелограмма,
построенного на векторах
численно
равна площади параллелограмма,
построенного на векторах
 и
и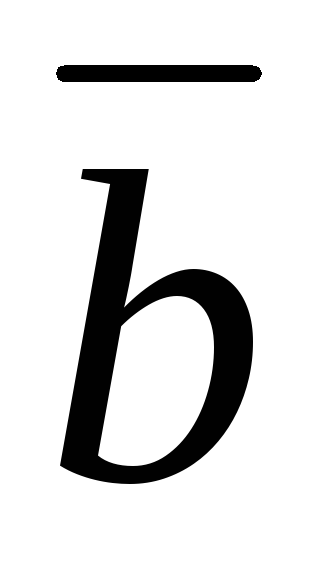 .
.
Доказательство следует из определения 16.
Векторное произведение векторов равно нулю тогда и только тогда, когда сомножители коллинеарны.
Доказательство аналогично свойству 5 скалярного произведения.
Векторное произведение антикоммутативно, т.е.
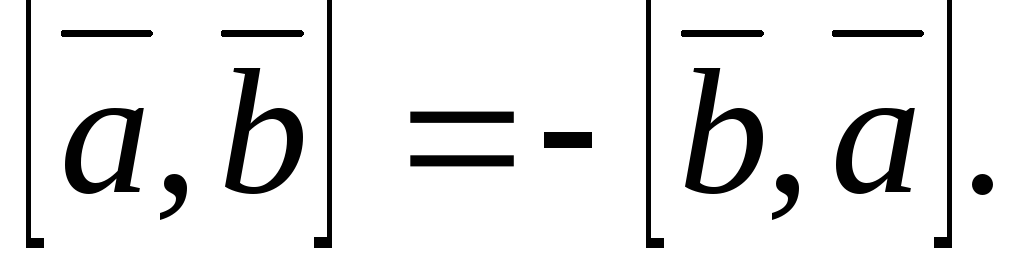
Доказательство.
Тройка
![]() – правая,
– правая,![]() – левая. Тройка будет правой, если
изменить направление
– левая. Тройка будет правой, если
изменить направление![]() ,
т.е.
,
т.е.![]() ∎
∎
Пример. Если
![]() – правая тройка, то
– правая тройка, то
![]()
![]()
![]()
Далее базис всегда будем рассматривать правый.
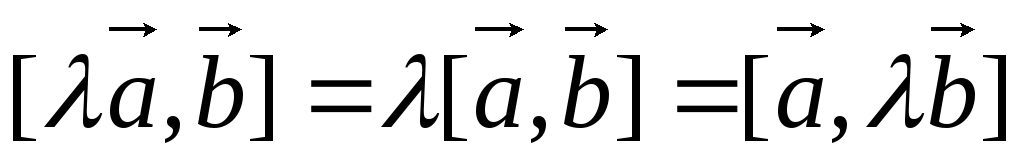 .
.
Докажем первое равенство.
Вначале покажем равенство модулей.
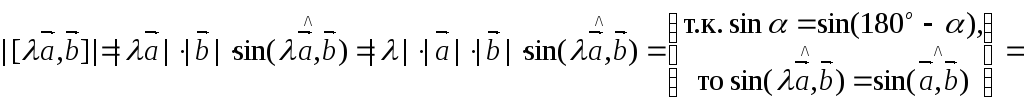
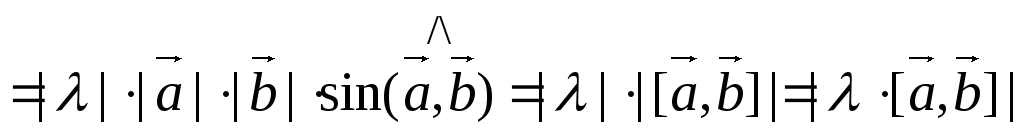 .
.
Так как
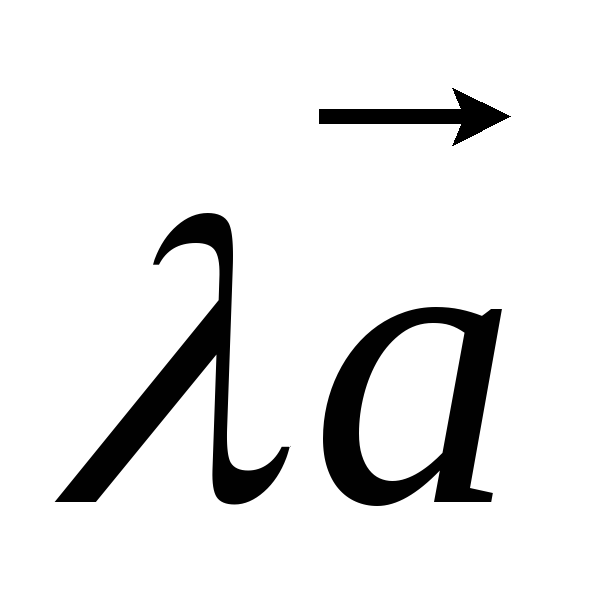 ||
|| ,
то
,
то
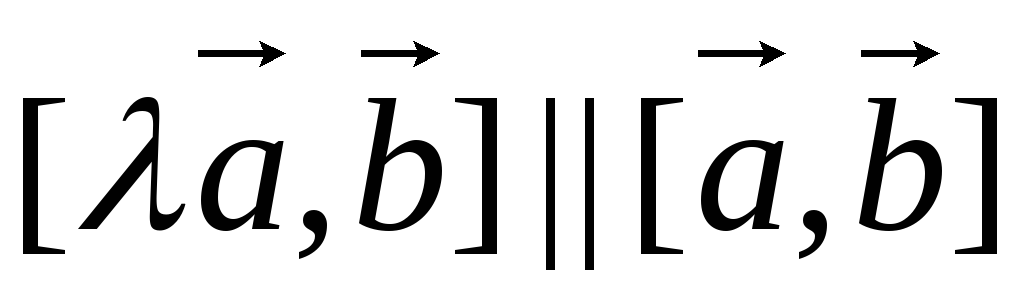

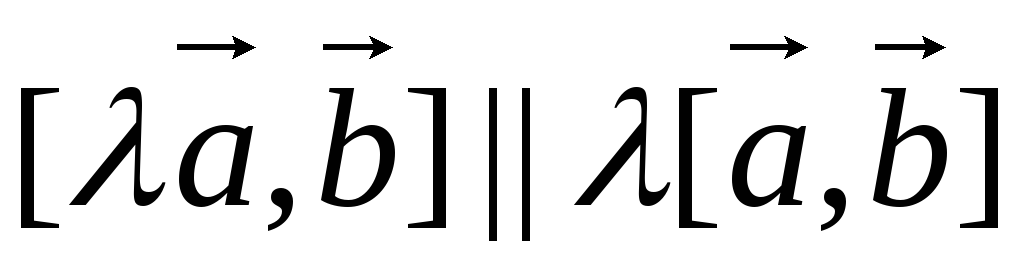 .
.Покажем, что
 .
Рассмотрим случай
.
Рассмотрим случай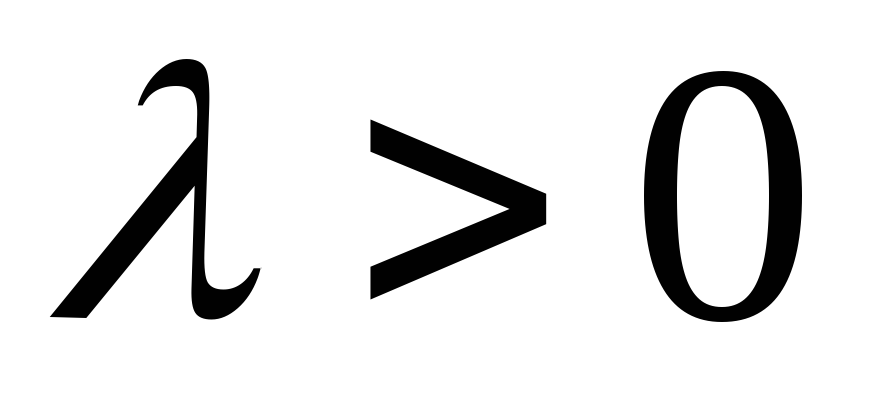 и
и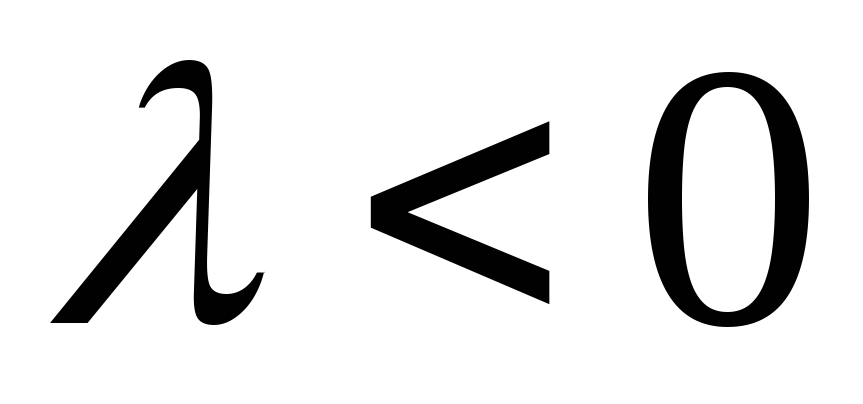 .
.
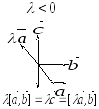
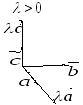
Отсюда вытекает доказываемое свойство.
Определение 17.
Смешанным
произведением векторов
![]() называется
число
называется
число
![]()
Обозначение:
![]()
Свойства смешанного произведения
Смешанное произведение некомпланарных векторов
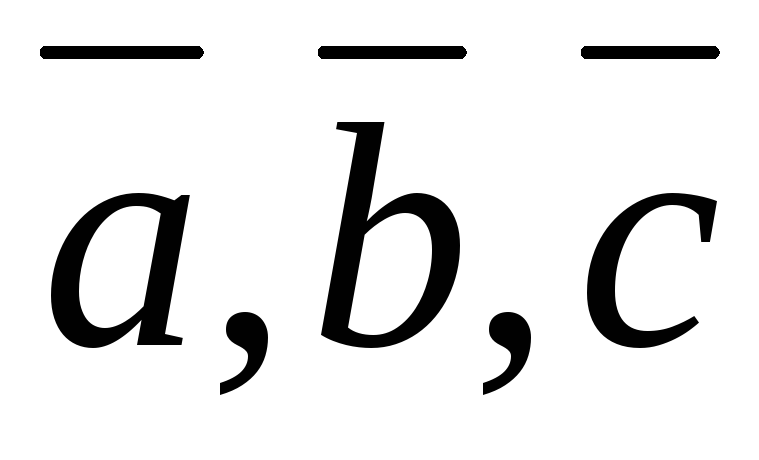 по модулюравно
объему параллелепипеда, построенного
на сомножителях. Оно положительно, если
тройка
по модулюравно
объему параллелепипеда, построенного
на сомножителях. Оно положительно, если
тройка
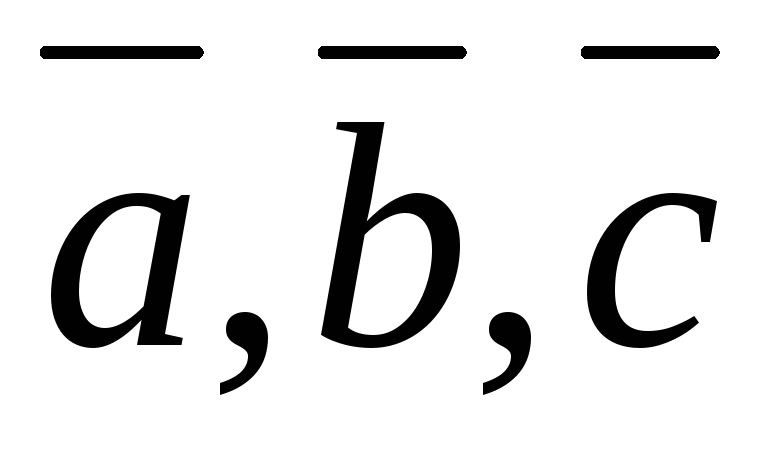 правая, и
отрицательно, если она левая.
правая, и
отрицательно, если она левая.
Доказательство.
Д ействительно,
объем параллелепипеда, построенного
на векторах
ействительно,
объем параллелепипеда, построенного
на векторах![]() равен произведению площади основания
равен произведению площади основания
![]() на высоту
на высоту![]() где
где![]() – угол между
– угол между![]() и
и![]()
Поэтому
![]()
Знак смешанного
произведения совпадает со знаком
![]() и поэтому, смешанное произведение
положительно, когда
и поэтому, смешанное произведение
положительно, когда![]() направлен с
направлен с![]() в одну сторону от плоскости векторов
в одну сторону от плоскости векторов
![]() т.е. тройка
т.е. тройка![]() – правая. Аналогично, смешанное
произведение левой тройки векторов
отрицательно.
∎
– правая. Аналогично, смешанное
произведение левой тройки векторов
отрицательно.
∎
Три вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю.
Доказательство. Если один из векторов нулевой, то свойство очевидно.
Пусть
![]() ,
,![]() ,
,![]()
0.
0.
![]() Пусть
Пусть
![]() ,
,![]() ,
,![]() – компланарны. Тогда
– компланарны. Тогда
![]()
![]()
![]()
![]() .
.
![]() Пусть
Пусть
![]()
либо
либо
![]()
![]() ,
либо
,
либо
![]() .
.
В
первом случае это означает, что вектор
![]()
векторам
векторам
![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() – компланарны. Во втором случае –
– компланарны. Во втором случае –![]() ||
||![]()
![]() и
и![]() – линейно зависимы
– линейно зависимы
![]() ,
,![]() ,
,![]() – компланарны.
– компланарны.
Смешанное произведение не зависит от группировки сомножителей, т.е.
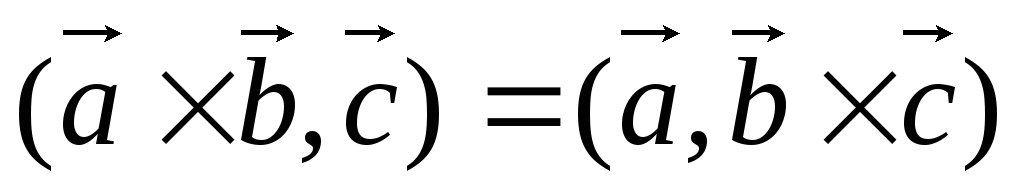 .
.
Доказательство.
Тройки
![]() ,
,![]() ,
,![]() и
и![]() ,
,![]() ,
,![]() ориентированы одинаково, значит знак
смешанного произведения одинаковый.
Модуль так же одинаковый в силу свойства
1.
ориентированы одинаково, значит знак
смешанного произведения одинаковый.
Модуль так же одинаковый в силу свойства
1.
Обозначение.
Смешанное произведение векторов
![]() ,
,![]() ,
,![]() обозначается
обозначается![]() ,
,
![]() .
.
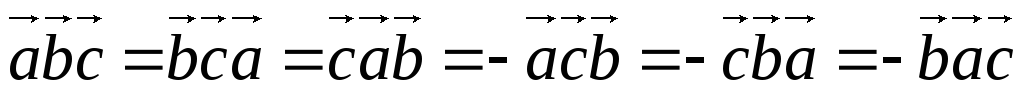 .
.
Следует из свойства циклической перестановки ориентированных векторов.
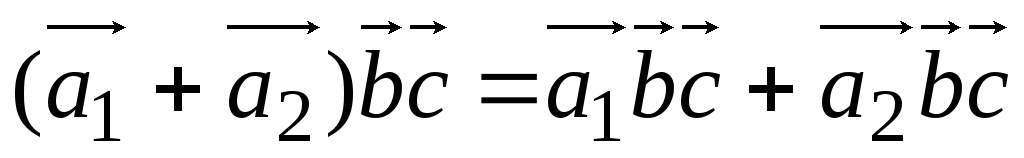 ,
,
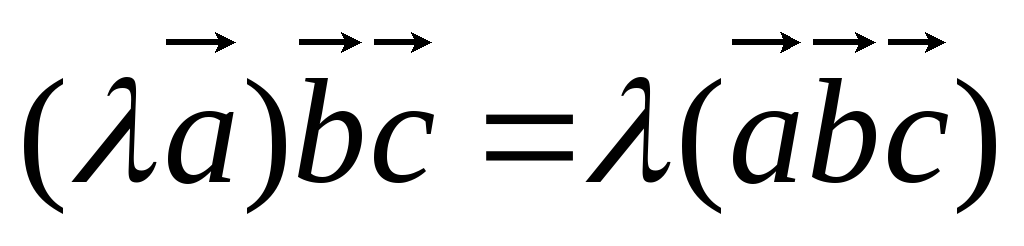 .
.
Следует из свойств скалярного произведения.
Теорема 5
(линейность векторного произведения).
Для любых векторов
![]() и любых чисел
и
имеет место равенство:
и любых чисел
и
имеет место равенство:![]()
Доказательство. Воспользуемся линейностью смешанного произведения по второму сомножителю:
![]()
Выбирая вместо
![]() вектора
вектора![]() ортонормированного базиса, можно видеть,
что координаты векторов
ортонормированного базиса, можно видеть,
что координаты векторов![]() и
и![]() равны, а значит, равны эти вектора.
∎
равны, а значит, равны эти вектора.
∎
60. Выражение векторного и смешанного произведения векторов через координаты сомножителей
Пусть в пространстве
векторов задан произвольный базис
![]() .
Пусть
.
Пусть![]() заданы своими координатами в этом
базисе, т.е.
заданы своими координатами в этом
базисе, т.е.
![]() .
.
Тогда
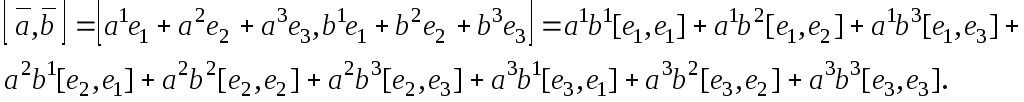 Так
как
Так
как![]() ,
то получаем
,
то получаем
![]()
В частности, если
базис – ортонормированный, т.е.
![]() то в силу
то в силу![]() ,
получаем
,
получаем
![]()
Это равенство формально можно переписать в виде
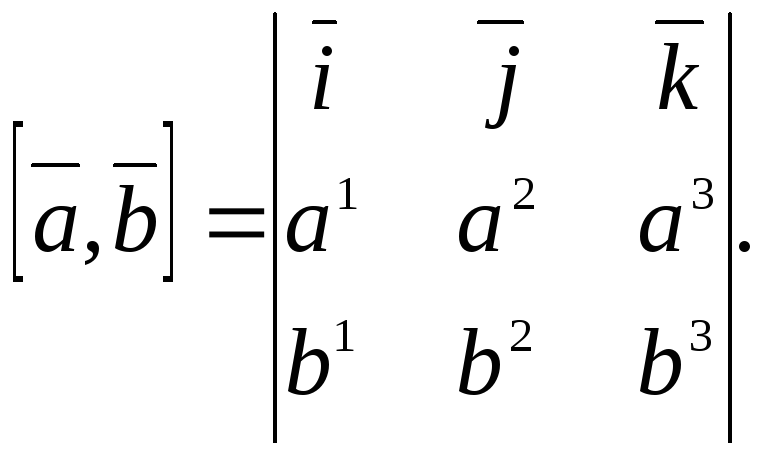
Если ввести в
рассмотрение третий вектор
![]() и вычислить смешанное произведение
векторов, то получаем:
и вычислить смешанное произведение
векторов, то получаем:
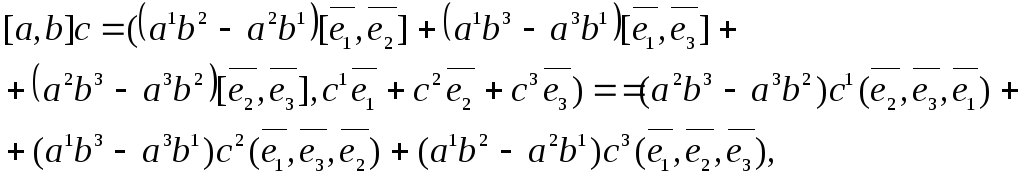
с учетом свойства равенства нулю смешанного произведения компланарных векторов. Отсюда следует, что
![]()
или, формально можно записать
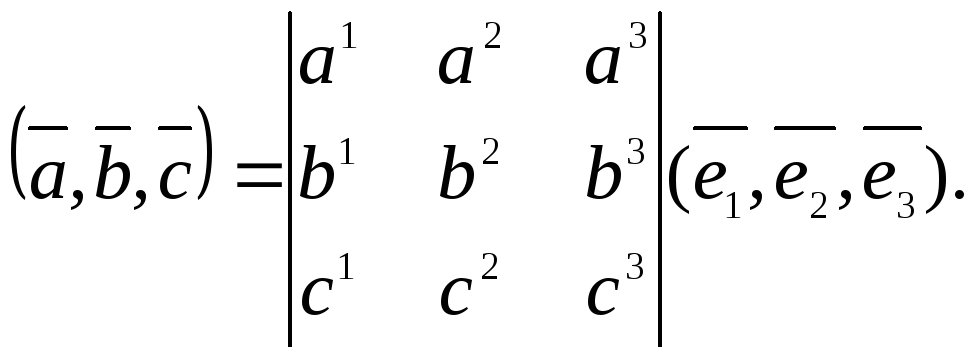
Если рассматриваемый
базис ортонормированный, то
![]()
70. Двойное векторное произведение.
Определение
18. Двойное
векторное произведение векторов
![]() ,
,![]() ,
,![]() это произведение вида
это произведение вида![]() .
.
Выразим двойное векторное произведение через скалярное.
Пусть
![]()
![]()
![]() и
и
![]()
![]() .
Тогда, в силу
.
Тогда, в силу
![]()
![]()
![]() лежит в плоскости векторов
лежит в плоскости векторов
![]() и
и
![]()
![]() .
Умножим это равенство скалярно на
.
Умножим это равенство скалярно на![]() .
Имеем
.
Имеем![]() .
.
Пусть
вектор
![]() не перпендикулярен одновременно векторам
не перпендикулярен одновременно векторам
![]() и
и
![]() (в противном случае
(в противном случае![]() в обоих случаях). Тогда
в обоих случаях). Тогда
![]()
![]()
![]() ,
такое что
,
такое что
![]() ,
,![]() .
.
Тогда
![]() .
.
Для
того, чтобы найти
![]() ,
вычислим левую и правую части в некотором
базисе. Пусть вектор
,
вычислим левую и правую части в некотором
базисе. Пусть вектор![]() направлен вдоль вектора
направлен вдоль вектора![]() ,
,![]() лежит в плоскости векторов
лежит в плоскости векторов
![]() и
и
![]() ,
,![]() определяется из условия, что
определяется из условия, что![]() ,
,![]() ,
,![]() образуют правую тройку. Тогда
образуют правую тройку. Тогда
![]() ,
,
![]() ,
,
![]() .
.
Имеем
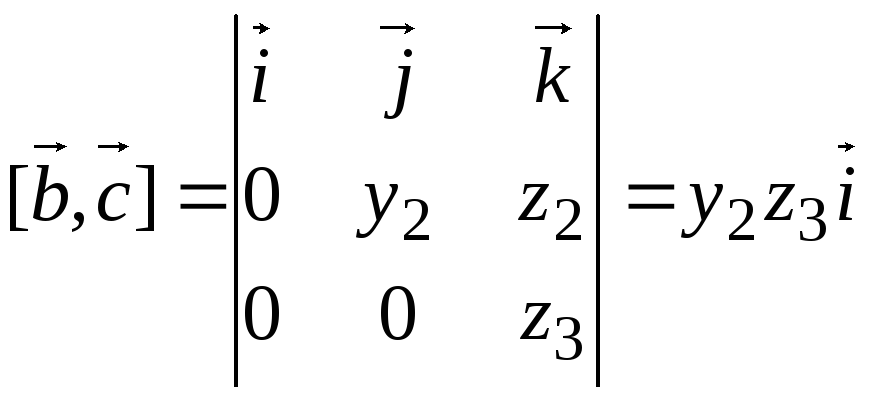 ,
,
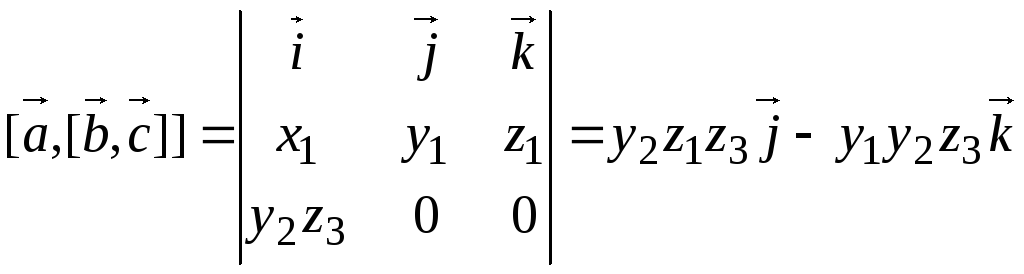 .
.
![]() .
.
![]() .
.
Отсюда
видно, что
![]() .
Итак, справедлива формула:
.
Итак, справедлива формула:
![]() .
.
Пример 1. Доказать тождество Якоби:
![]() .
.
Имеем
![]() ,
,
![]() ,
,
![]() .
.
Суммируя эти равенства, получим тождество Якоби.
Пример
2. Вычислить
![]() .
.
Имеем:
(![]() )
)![]()
![]() .
.
80. Примеры решения задач.
Пример
1. Вычислить
синус угла между векторами
![]() ,
,![]() .
.
Имеем:
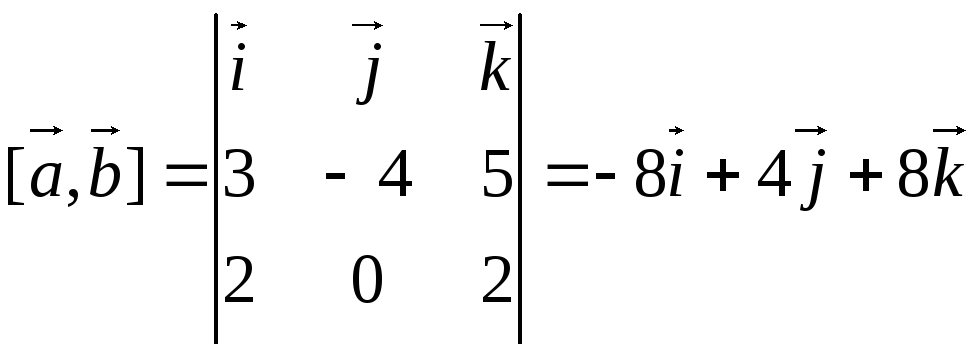 .
.
![]() .
.
![]() .
.
Пример
2. Вычислить
площадь параллелограмма, построенного
на векторах
![]() ,
,
![]() .
Так как модуль векторного произведения
численно равен площади параллелограмма,
построенного на перемножаемых векторах,
то имеем
.
Так как модуль векторного произведения
численно равен площади параллелограмма,
построенного на перемножаемых векторах,
то имеем
![]() .
.
Если
параллелограмм расположен в плоскости,
то
![]() и
и
![]() .
.
П
![]()
![]()
![]() ,
,![]() ,
,![]() .
Имеем
.
Имеем
![]()
![]()
![]()

![]()
![]()

 .
Но
.
Но
![]()
![]()
![]()
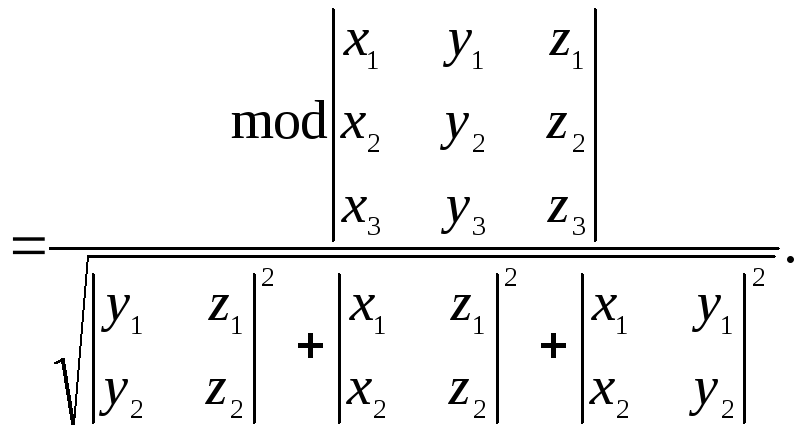 .
.
