ТАУ-2_УТС СУХТП

1 Динамические характеристики линейных систем.

Для оценки динамических свойств объекта, регулятора и других звеньев АСР широко применяются различные динамические характеристики.

Динамическая характеристика – это реакция звена на некоторое стандартное или, так называемое, типовое входное воздействие. По экспериментально полученным динамическим характеристикам можно, как правило, определить передаточную функцию.

В ТАУ широко применяются два вида динамических характеристик: временные и частотные.

1.1 Временные характеристики.

Из временных наиболее часто используются импульсная и переходная характеристики

1.1.1 Переходная характеристика

Переходной характеристикой h(t) называется реакция звена (или системы) на единичное скачкообразное воздействие при нулевых начальных условиях.

hуст=K t

Рис.7.1.Примеры переходных характеристик

Напомним, что при нулевых начальных условиях в момент подачи входного сигнала звено находится в статическом режиме (входные и выходные сигнала не изменяются во времени) Установившееся значение h(t) равно коэффициенту усиления звена

Действительно из уравнения статики при x =1 получаем y=Kx=K.

На рис. 7.1 приведены примеры переходных характеристик устойчивых звеньев и единичное скачкообразное воздействие x(t) =1(t) .

Переходная характеристика может быть вычислена по передаточной функции, например, решением соответствующего дифференциального уравнения.

Существуют методы, позволяющие по экспериментально полученной переходной кривой определить передаточную функцию. Что широко применяется на практике.

1.2 Частотные характеристики

Подадим на вход линейного устойчивого звена гармонический сигнал

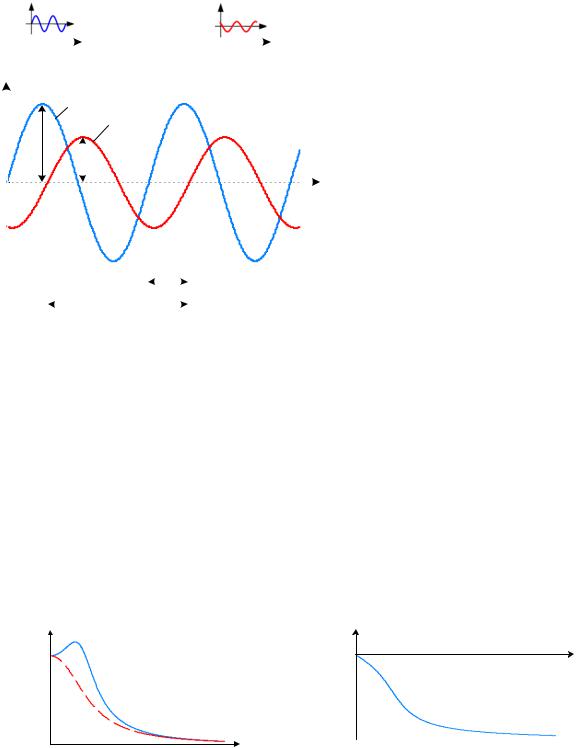
После окончания переходного процесса на выходе получим установившийся гармонический сигнал той же частоты, но другой амплитуды и сдвинутый по фазе на угол ϕ по сравнению с

входным

Рис.7.2.К экспериментальному определению частотных характеристик

Если изменять частоту входного сигнала, оставляя амплитуду постоянной, то будет изменяться амплитуда выходного сигнала и сдвиг по фазе между входными и выходными колебаниями.

Зависимость отношения амплитуды выходного сигнала к амплитуде входного от частоты называется амплитудно-частотной характеристикой АЧХ

Зависимость сдвига фаз между выходными и входными колебаниями называется фазочастотной характеристикой ФЧХ

Примеры графиков АЧХ и ФЧХ приведены ниже

?

Рис.7.3. Примеры частотных характеристик

Для большинства физически реализуемых звеньев АЧХ с ростом частоты убывает, а фазовый сдвиг отрицателен (отставание по фазе).

Значение A(ω) характеризует усиление по амплитуде гармонического сигнала частоты ω. Важную роль играет амплитудно-фазовая характеристика (АФХ) определяемая формулой

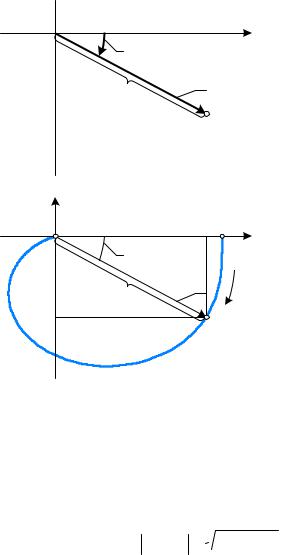
Формально W(jω) – комплексный вектор, длина (модуль) которого равен A(ω), а угол c вещественной осью равен φ(ω). Формула (7.6) является показательной формой записи комплексного числа. При изменении частоты ω в пределах 0≤ω≤∞ изменяется длина вектора и угол, а конец вектора описывает кривую, которая собственно и называется амплитудно-фазовой характеристикой – АФХ, рис.7.4.

Im W(jω)

Re W(jω)

φ(ω1)

A(ω1) W(jω1)

где ReW ( jω) , ImW ( jω) - вещественная и мнимая частотные характеристики – проекции вектора

W(jω) на оси координат. Формулы связи:

A(ω) = W ( jω) = Re2 +Im2

ReW ( jω) = A(ω) cosϕ(ω)

ImW ( jω) = A(ω) sin ϕ(ω)

2 Типовые динамические звенья.

Типовыми – называются звенья, с передаточными функциями порядка не выше второго. Многие реальные звенья можно описать как простейшие типовые. Любое более сложное звено (более высокого порядка) можно представить как некоторое соединение типовых.

Все звенья можно разделить на три группы:

1.Статические (пропорциональные, усилительные)

2.Дифференцирующие

3.Интегрирующие

Динамические характеристики каждой группы звеньев характеризуются общими свойствами. Рассмотрим простейшие типовые звенья и их характеристики.

2.1 Статические звенья.

К –постоянная – коэффициент усиления или коэффициент передачи.

Простейшим примером может служить делитель напряжения или рычаг, рис. 8.1.

R1

и изображена на рис.8.2. Выходной сигнал усиливается в К раз по сравнению со входным. Напомним, что переходная характеристика есть реакция на единичное скачкообразное воздействие при нулевых начальных условиях (см. раздел 7.1.)

x(t)=1(t) 1

t

y(t)=h(t)

K

t

Рис. 8.2. Переходная характеристика усилительного звена

где τ – запаздывание.

Выходной сигнал повторяет входной со сдвигом во времени (запаздыванием) на время τ.. Передаточная функции звена

Выражение для передаточной функции имеет не совсем обычный вид, его можно получить, если выражение x(t −τ) разложить в ряд Тейлора относительно t и перейти к операторной форме

записи.

Переходная характеристика изображена на рис. 8.3 и описывается уравнением

Примером может служить транспортер для перемещения сыпучих материалов

Cвязь между входными и выходными потоками описывается уравнением

Qвых(t) = Qвх (t −τ) ,

где τ = vl ., l – длина ленты, v – скорость перемещения.

Другой пример – прокатка стали

Толщина листа может быть измерена только на определенном расстоянии от валов, что приводит к запаздыванию измерения по времени.

Транспортное запаздывание характерно для трубопроводов. Импульс давления, возникший в начале участка трубы, достигает конечной точки через некоторое время, зависящее от скорости звука в среде.

Переходная характеристика приведена на рис. 8.2

Передаточная функция может быть разложена на произведение двух сомножителей. Тогда звено 2-го порядка можно представить в виде последовательного соединения двух апериодических звеньев 1-го порядка, рис. 8.4.

Рис. 8.4. Эквивалентная структурная схема апериодического звена 2-го порядка

Примером может служить каскад из двух емкостей, рис. 8.5.

Входным сигналом является приток в первую емкость, выходным – уровень во второй.

Qп

Установившаяся составляющая, как и в случае инерционного звена, равна yуст (t) = K . Постоянные

График переходного процесса изображен на рис. 8.6-а. Поскольку начальная скорость равна нулю, y(1) (0) = 0 , то в начальный момент переходная кривая касается оси времени. Переходный процесс

затухает медленнее, чем в инерционном звене – пунктирная кривая на рис. 8.6-а.

Звено называется колебательным, если корни характеристического уравнения комплексносопряженные. Это возможно, если T1 < 2T2 .

Передаточная функция колебательного звена обычно записывается в другой форме

T – постоянная времени; T2 =T , T1 = 2ξT .

Корни характеристического полинома (комплексно сопряженные)

Переходная характеристика получается аналогично предыдущему звену. Только комплексносопряженные корни дают гармоническую составляющую переходного процесса

Рис.8. 6. Переходные характеристики звеньев 2-го порядка

С уменьшением коэффициента демпфирования ξ, колебательность переходного процесса возрастает.

Примеры колебательных звеньев приведены на рис. 8.7.

Рис. 8.7. Примеры колебательных звеньев

При ξ=0 в системе возникают незатухающие колебания, рис.8.9., такое звено называется консервативным . Передаточная звена принимает вид

Корни характеристического полинома чисто мнимые – граница устойчивости.

Примером консервативного звена служит математический маятник при отсутствии трения. x(t)

t

h(t)

K

t

Рис. 8.9. Переходная характеристика консервативного звена

Вернемся к примерам на рис.8.8. В случае, если значение сопротивления R велико, потери энергии на нем увеличиваются (превращаются в тепло) и звено становится апериодическим. Если же R = 0, то потери отсутствуют, имеем идеальное консервативное звено – колебания не затухают. Аналогичная ситуация имеет место и в случае с гидромеханическим демпфером. Если воздействовать на груз с некоторой постоянной силой (например, электромагнитом), то груз преодолев сопротивление пружины и вязкое трение перейдет в новое положение. Если вязкость масла не велика, то переходный процесс будет колебательным, при высокой вязкости масла процесс будет апериодическим. При отсутствии трения получим консервативное звено.

Отметим, что установившееся значение переходной характеристики всех устойчивых статических звеньев равно коэффициенту усиления – hуст = K .

2. Реальное дифференцирующее звено.

Реальное дифференцирующее звено может быть представлено последовательным соединением звеньев: идеального дифференцирующего и инерционного. Его передаточная функция имеет вид

Характеристический полином

D(s) =Ts +1,

корень характеристического полинома s1 = −T1 , звено устойчивое.

Переходная характеристика