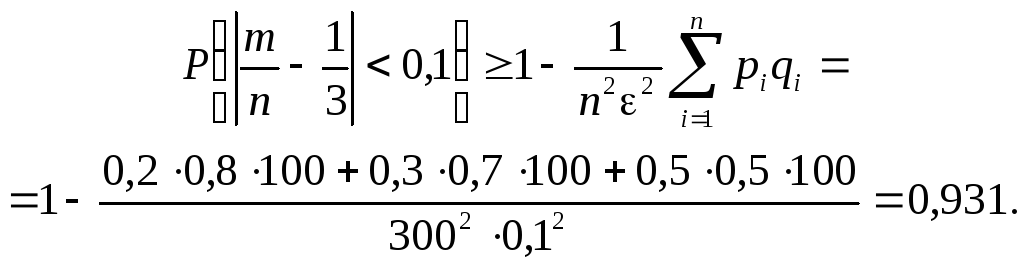Задачи.

15. Последовательность независимых случайных величин {X_n} задана законом распределения

Xn		–
P

Применим ли к заданной последовательности теорема Чебышева?

16. Выяснить, применима ли теорема Чебышева к последовательности независимых случайных величин {X_n}, если закон распределения имеет вид

а)	Xn	–n2		n2
	P
б)	Xn	–n		n
>0	P

17. Последовательность независимых случайных величин {X_n} задана законом распределения

Xn	n+1	– n
P

Убедится, что требование равномерной ограниченности дисперсий для данной последовательности случайных величин не выполняется. Можно ли отсюда заключить, что закон больших чисел для этой последовательности не применим?

18. Последовательность независимых случайных величин {X_n} задана законом распределения

Xn		0
P

Применим ли к заданной последовательности теорема Хинчина?

19. Пусть X_n – случайная величина, которая с одинаковой вероятностью может принимать одно из двух значений k^s или –k^s. При каком s к среднему арифметическому последовательности {X_n} таких независимых случайных величин применим закон больших чисел?

20. Доказать теорему Маркова: если дисперсии произвольных случайных величин в последовательности {X_n} удовлетворяет условию (6), то имеет место утверждение (7).

21. Выяснить, применима ли теорема Маркова к последовательности случайных величин {X_n}, если закон распределения имеет вид

а)	Xn	–lnn	lnn
	P
б)	Xn
>0	P

22*. Доказать, что к последовательности случайных величин, в которой каждая величина может зависеть только от величин со смежными номерами, применим закон больших чисел, если только все случайные величины последовательности имеют конечные дисперсии и математические ожидания.

23**. Дана последовательность случайных величин {X_n}, для которых D[X_n]C и r_ij0 при |i–j| (где r_ij – коэффициент корреляции между X_i и X_j). Доказать, что к данной последовательности применим закон больших чисел (теорема Бернштейна).

4

Теорема Бернулли. Если в каждом из n независимых испытаний вероятность p появления события A постоянна, то при достаточно большом числе испытаний отклонение относительной частоты от вероятности p будет сколь угодно малым

. (11)

Соответствующее неравенство Чебышева имеет вид

. (12)

Теорема Пуассона. Если в последовательности независимых испытаний вероятность появления события A в i-м испытании равна p_i, то

, (13)

где – средняя арифметическая вероятность.

Соответствующее неравенство Чебышева имеет вид

. (14)

Пример 9. Вероятность наличия зазубрины на металлических брусках, заготовленных для обточки, равна 0,2. Оценить вероятность того, что в партии из 1000 брусков отклонение числа пригодных брусков от800 не превышает 5%.

Решение. Из условия задачи следует, что n=1000, =0,05, q=0,2, p=1–q=0,8. В соответствии с формулой (12), получим

.

Пример 10. Сколько раз нужно подбросить монету, чтобы с вероятностью, не меньшей 0,997, можно было утверждать, что относительная частота выпадения герба будет между 0,499 и 0,501?

Решение. По условию задачи требуется рассмотреть неравенство

.

Поскольку =0,001, p=0,5, q=0,5, то получим

.

Следовательно, требуемое условие будет выполняться, если монету подбросить не менее 8333334 раз.

Пример 11. Стрельба по цели ведется поочередно из трех орудий, причем вероятности попадания в цель равны соответственно 0,2, 0,3 и 0,5. Таким образом произведено 300 выстрелов. Оценить вероятность того, что при этом относительная частота отличается от средней вероятности попадания по абсолютной величине не более чем на 0,1.

Решение. Найдем среднюю вероятность попадания в цель при 300 выстрелах:

.

Таким образом, в задаче требуется оценить вероятность

.

Более точная оценка будет иметь следующий вид