
Лекции по компьютерной графике
.pdf
Климентьев К.Е. Компьютерная графика (курс лекций).
Рис. 21. Золотое сечение
Пусть P=0.5. Разделим каждый из отрезков в этой пропорции и соединим центральные точки новым отрезком. Полученные три отрезка вновь разделим в пропорции P=0.5 и так далее. Линия, к которой стремится множество отрезков – кривая Безье (см. рис. 22).
Рис. 22. Этапы построения кривой Безье
3.2. АЛГОРИТМЫ ЗАКРАШИВАНИЯ ФИГУР
Будем считать, что фигура ограничена контуром, т.е. непрерывной кривой, цвет которой отличен от цвета внутренней части фигуры. Существуют универсальные алгоритмы закрашивания “полигонов”, т.е. многоугольников, заданных произвольным количеством вершин, но у них есть недостатки, связанные с неоднозначностью представления (см. рис. 23).
Рис. 23. Все эти фигуры заданы одним и тем же множеством вершин
Поэтому стараются сводить задачу закрашивания сложных фигур к закрашиванию множества простых выпуклых фигур (например, треугольников).
3.2.1. РЕКУРСИВНЫЙ АЛГОРИТМ С “ЗАТРАВКОЙ”
Шаг 1. Ставится точка нужного цвета (“затравка”) где-то внутри фигуры, она считается текущей.
Шаг 2. Проверяются поочередно все “соседи” для текущей точки, и если их цвет отличается от цвета закраски и цвета контура, то каждая такая точка закрашивается и сама становится текущей (с рекурсивным переходом на Шаг 2).
Этот алгоритм рекурсивный и приводит к большим затратам стековой памяти, поэтому его целесообразно использовать только для закраски небольших фигур.
3.2.2. ПОСТРОЧНЫЙ АЛГОРИТМ
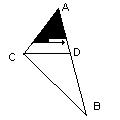
Этот алгоритм используется в предположении, что любая сложная фигура может быть покрыта множеством маленьких треугольников. Вершины сортируются таким образом, чтобы образовались два треугольника (ADC и CDB) с общим горизонтальным основанием (CD), находится уравнение этого основания. Далее, двигаясь с шагом 1 по координате Y вплоть до основания (CD), проводятся отрезки горизонтальных линий от точек одной
21
Климентьев К.Е. Компьютерная графика (курс лекций).
стороны (AC) до точек другой (AD). Затем это действие повторяется для двух других пар отрезков (CB и DB).
Рис. 24. Построчная закраска треугольника
Справка: если две прямых заданы уравнениями вида A1*X+B1*Y+C1=0 и A2*X+B2*Y+C2=0, то точка их пересечения имеет координаты:
| B1 |
C1 |
| |
| C1 |
A1 |
| |
||
| B2 |
C2 |
| |
| C2 |
A2 |
| |
||
X0= --------- |
Y0 = --------- |
||||||
| |
A1 |
B1 |
| |
| |
A1 |
B1 |
| |
| |
A2 |
B2 |
| |
| |
A2 |
B2 |
| |
3.3. МАТРИЧНЫЕ ПРЕОБРАЗОВАНИЯ ФИГУР НА ПЛОСКОСТИ
Будем рассматривать каждую точку с координатами (X,Y) как вектор-столбец из 3 элементов, а преобразования этой точки как матрицу 3x3, которая умножается на этот вектор, чтобы получить новые, преобразованные координаты (X’,Y’) точки:
abc |
X |
aX +bY + c |
|
X ' |
|||||
|
|
|
|
|
|
|
|
|
|
def |
|
× Y |
= dX + eY + f |
|
= Y ' |
||||
|
|
|
|
|
+ 0 |
+1 |
|
|
|
001 |
1 |
|
0 |
|
1 |
|
|||
Возможны несколько элементарных преобразований, остальные – это их комбинации. Это – аффинные (т.е. линейные) преобразования.
1. Масштабирование по осям. Задается матрицей и приводит к системе преобразований:
K x |
0 |
0 |
|
X '= K x X |
|
||
|
0 |
K y |
0 |
→ |
, |
||
|
|||||||
|
|
|
|
|
Y '= K yY |
|
|
|
0 |
0 |
|
|
|
|
|
|
1 |
|
|
|
|||
где Kx и Ky– коэффициенты изменения масштаба. В частности, при Kx =1и Ky=1 имеем тождественное преобразование; при Kx = -1 и Ky=1 имеем симметричное отражение относительно оси X; при Kx = 1 и Ky= -1 имеем симметричное отражение относительно оси Y; при Kx = -1 и Ky= -1 имеем центрально-симметричное отражение относительно начала координат. Прочие значения Kx и Ky задают изменения линейных расстояний точки относительно начала координат.
2.Поворот относительно начала координат на угол ϕ. Задается матрицей и приводит к системе преобразований:
22

Климентьев К.Е. Компьютерная графика (курс лекций).
cosϕ |
sinϕ |
|
|
|
cosϕ |
−sinϕ |
||
|
0 |
0 |
|
||
0
X '= X cosϕ +Y sinϕ 0 → Y '= −X sinϕ +Y cosϕ 1
Рис. 25. Поворот точки
3. Сдвиг. Задается матрицей и приводит к системе преобразований:
1 0
0 10 0
∆x |
|
X '= X + ∆x |
|
∆y |
|
||
→ |
|||
|
|
Y '= Y + ∆y |
|
1 |
|
|
|
|
|
Аналогичные преобразования есть и для трехмерного пространства, они задаются матрицами
4х4.
Главное свойство матричных преобразований: любое преобразование точки относительно начала координат может быть представлено как обратное преобразование начала координат относительно этой точки.
Пример 1. Составить преобразование для поворота точки с координатами (X,Y) относительно точки с координатами (X0,Y0) на угол ϕ. Это преобразование есть комбинация следующих:
•сдвиг начала координат в точку (X0,Y0);
•поворот точки (X,Y) на угол ϕ;
•возврат начала координат в точку (0,0).
С учетом главного свойства матричных преобразований:
1 |
0 |
− X 0 |
|
|
cosϕ |
sinϕ |
0 |
|
|
1 |
0 |
X 0 |
|
||
A = 0 |
1 |
−Y |
|
|
B = −sinϕ |
cosϕ |
0 |
C = |
0 |
1 |
Y |
|
|||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
0 |
0 |
|
|
|
|
|
1 |
|
0 0 |
|
|
|
|
1 |
|
|
0 0 |
|
||||||
Рассчитываем общее преобразование D: |
|
|
|
|
|
|
|
||||||||
|
|
|
cosϕ |
|
sinϕ |
X 0(1−cosϕ) −Y0 |
sinϕ |
|
|
||||||
D = A× B |
×C = |
−sinϕ |
|
cosϕ |
Y (1−cosϕ) + X |
0 |
sinϕ |
|
|
||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Эту матрицу можно рассчитать однократно, и затем многократно использовать.
23

Климентьев К.Е. Компьютерная графика (курс лекций).
3.4. ТРЕХМЕРНАЯ ГРАФИКА
Предметная область изображения трехмерных сцен включает следующие сущности (см. рис. 27).
Рис. 27. Трехмерная сцена
3.4.1. МАТРИЧНЫЕ ПРЕОБРАЗОВАНИЯ ОБЪЕМНЫХ ФИГУР
Для 3D-графики матричные преобразования задаются матрицами 4x4:
K x cosα cosγ |
||
|
sin γ |
|
|
||
sinα |
||
|
||
|
0 |
|
|
||
−sin γ
K y cos β cosγ sin β
0
−sinα |
∆X |
−sin β |
|
∆Y |
|
K z cos β cosα |
∆Z |
0 |
|
1 |
В этой обобщенной матрице ∆X, ∆Y, ∆Z – сдвиги по осям; Kx, Ky, Kz – коэффициенты масштабирования по осям; α, β, γ - углы вращения вокруг осей Y, X, Z соответственно.
3.4.2. ПРОЕЦИРОВАНИЕ ОБЪЕМНЫХ ФИГУР НА ПЛОСКОСТЬ
Основные виды проецирования, применяемые в 3D-графике (см. рис. 28):
а) параллельное; б) параллельное аксонометрическое; в) перспективное Рис. 28. Виды проецирования
Основная задача проецирования: для точки известны ее координаты (X,Y,Z) в пространстве мировых координат, найти ее координаты (X’,Y’,Z’) в пространстве экранных координат (на плоскости проецирования).
24

Климентьев К.Е. Компьютерная графика (курс лекций).
1. Аксонометрическое проецирование. В лабораторных работах применять именно его!
Лучи проецирования перпендикулярны плоскости проецирования. Положение плоскости проецирования в мировых координатах задается двумя углами (см. рис. 29):
•α - это поворот относительно оси Z мировых координат;
•β - это “кивок” относительно плоскости XY мировых координат.
а) вид плашмя б) вид сбоку Рис 29. Взаимное положение систем координат в аксонометрии
Решение основной задачи проецирования:
X '= X cosα −Y sinα
Y '= X sinα cos β +Y cosα cos β − Z sin βZ '= X sinαsin β +Y cosαsin β + Z cos β
2. Перспективное (центральное) проецирование. Может быть представлено как
последовательная комбинация: 1) аксонометрического проецирования; 2) преобразования, корректирующего линейные размеры. Это преобразование зависит от мировой координаты
Zц центра симметрии (см. рис. 30): X’= X (Zц-Z’)/(Zц-Z) и Y’= Y (Zц-Z’)/(Zц-Z).
Рис. 30. Перспективное проецирование
3.4.3. МОДЕЛИ ОСВЕЩЕНИЯ ОБЪЕМНЫХ ФИГУР
В соответствие с моделью Уиттеда в общем случае интенсивность освещения точки, принадлежащей поверхности:
И= Ир + Им + Из,
1.Ир = И0=const - интенсивность рассеянного освещения, заполняющего пространство.
2.Им = И0 Kм cosθ – интенсивность освещения матовой поверхности точечным источником. Здесь И0 - интенсивность источника освещения; Kм - коэффициент материала; θ - угол между нормалью к поверхности в точке и углом на источник освещения. (Нормаль – перпендикулярный вектор единичной длины).
25

Климентьев К.Е. Компьютерная графика (курс лекций).
3. Из = И0 Kм cosnθ – интенсивность освещения зеркально отражающей поверхности точечным источником. Здесь n – константа в интервале 1÷200.
Вычисление cosθ (см. рис. 31).
Рис 31. К расчету cosθ
Пусть точка принадлежит некоторой плоскости. Выделим на ней произвольный треугольник, заданный тремя вершинами с координатами (x1,y1,z1), (x2,y2,z2) и (x3,y3,z3), а положение источника света - координатами (xс, yс, zс). Вместо вектора, указывающего на источник света, целесообразно рассматривать параллельный ему вектор с началом в одной из вершин треугольника, например (xs,ys,zs)=(xc-x1, yc-y1, zc-z1). Тогда координаты вектора нормали вычисляются как
xn=(y2-y1)(z3-z1)-(z2-z1)(y3-y1) yn=(z2-z1)(x3-x1)-(x2-x1)(z3-z1) zn=(x2-x1)(y3-y1)-(y2-y1)(x3-x1)
А косинус угла между векторами (xs,ys,zs) и (xn,yn,zn):
cosθ = |
xn xs + yn ys + zn zs |
. |
|
+ yn2 + zn2 )(xs 2 + ys 2 + zs 2 ) |
|||
(xn2 |
|
В модели Уиттеда вся грань закрашена одним цветом. В моделях Гуро и Фонга возможны плавные переходы закраски между гранями.
3.4.4. ПРИМЕРЫ ПОСТРОЕНИЯ ИЗОБРАЖЕНИЙ ОБЪЕМНЫХ ФИГУР
Объемные фигуры строятся в виде множества треугольных плоских граней, чем их больше, тем реалистичней изображение. Общая схема построения:
•рассчитать координаты вершин грани в мировых координатах;
•пересчитать координаты вершин грани в экранных координатах (с учетом поворота);
•удалить из рассмотрения невидимые (заслоненные) грани (см. ниже п. 3.4.5.);
•рассчитать интенсивность освещения грани с учетом положения источника освещения;
•изобразить грань в виде закрашенного треугольника.
а) Полный каркас; б) Видимые грани; в) Грани с шагом 30°; г) Грани с шагом 10° Рис. 32. Изображения объемных фигур
1. Цилиндр. Произвольная точка поверхности цилиндра (см. рис. 33) параметрически
26

Климентьев К.Е. Компьютерная графика (курс лекций).
описывается соотношениями:
x = R sin α y = R cos α z = H h
Рис. 33. Цилиндр
Здесь R – радиус торца; H-высота цилиндра; 0<α<360° - параметр приращения долготы; 0.5<h<0.5 – параметр приращения высоты.
2. Сфера. Произвольная точка поверхности сферы (см. рис. 34) параметрически описывается соотношениями:
x= R cosα sinβ
y= R cosα cosβ
z= R sinα
Рис. 34. Сфера
Здесь R-радиус сферы; -90°<α<90°- параметр приращения широты; 0<β<360° - параметр приращения долготы.
3. Тор. Произвольная точка поверхности тора (см. рис. 35) параметрически описывается соотношениями:
x= (R1+R2 cosα) sinβ
y= (R1+ R2cosα) cosβ
z= R1 sinα
Рис. 35. Тор
Здесь R1-радиус тора; R2 – толщина кольца; -90°<α<90°- параметр приращения широты; 0< β<360° - параметр приращения долготы.
27

Климентьев К.Е. Компьютерная графика (курс лекций).
Модифицируя закон, по которому изменяются те или иные координаты объекта, возможно получать различные искажения формы объекта. Например, изменяя радиус R объекта “цилиндр” в зависимости от значения текущей координаты z по формуле
R=(A*(R*z)+B) mod M,
Можно построить фигуру типа “елочка” (см. рис. 36). Здесь A, B и M
– некоторые константы.
Рис. 36. Елочка
3.4.5. УДАЛЕНИЕ НЕВИДИМЫХ ФРАГМЕНТОВ
1. “Алгоритм художника“ – заключается в том, что сначала изображаются удаленные объекты, потом более близкие, благодаря этому они “загораживают” друг друга. Недостаток
– невозможность применения для изображения некоторых сцен (см рис. 37).
Рис. 37. Невозможно изобразить при помощи “алгоритма художника”
2. Метод “плавающего” горизонта” - заключается в том, что сначала изображаются ближние объекты, а потом “высовывающиеся” фрагменты более дальних объектов. Это возможно, если известны аналитические описания объектов (например, уравнения сечений поверхности, см. рисунок 38), позволяющие рассчитать “высовывающиеся” части.
Рис. 38. Перекрытие сечений
3. Метод “Z-буфера” - заключается в том, что для экрана заводится массив Z “глубин” для каждой точки. В начале он инициализируется значениями -∞. Необходимость изображать точку с мировыми координатами (x, y, z) проверяется так:
Function Изобразить_Ли_Точку(x, y, z):boolean; Begin
If Z[x,y]<z
Then begin Z[x,y]:=z; Изобразить_Ли_Точку := TRUE End; (*Заслонить далекую*) Else Изобразить_Ли_Точку := FALSE; (*Не заслонять более близкую*)
End;
4. Метод обратной трассировки лучей – универсальный аналитической метод полного просчета трехмерных сцен. Заключается в том, что для каждой точки изображаемых объектов рассчитываются вектора, направленные на камеру (глаз) и на источники освещения, и в результате этого определяется, нужно ли изображать точку, какова интенсивность ее закрашивания и т.п. Существует большое количество сопутствующих
28

Климентьев К.Е. Компьютерная графика (курс лекций).
методов, упрощающих и ускоряющих расчеты. Например, метод оболочек предусматривает построение для каждого объекта “оболочки” - простой фигуры (шара или куба), содержащей внутри себя объект. На первом этапе расчета анализируются взаимные расположения не объектов, а их оболочек, и только если одна оболочка загораживает другую, выполняется более подробный расчет; в противном случае фигуры считаются удаленными и не загораживающими друг друга.
Каркас шара можно строить с использованием модификации метода Z-буфера: изображать только те грани, у которых нет вершин с отрицательной координатой z. Закрашенный шар можно строить с использованием модификации “алгоритма художника”: обход углов широт вести так, чтобы сначала рисовались “задние” грани, а потом “передние”.
ТЕМА 4. ФОРМАТЫ ХРАНЕНИЯ ИЗОБРАЖЕНИЙ
Основные задачи хранения изображений:
•обеспечить минимальный объем данных;
•обеспечить легкость манипулирования изображениями.
Для уменьшения объема данных, представляющих изображения, используются различные методы сжатия данных. Качество методов определяется коэффициентом сжатия:
Ксж = N/Nсж,
Где N – объем данных до сжатия; Nсж - после сжатия.
Две больших группы методов:
•без потерь информации (т.е. исходная информация может быть полностью восстановлена после раскодировки из сжатого состояния);
•с потерями части незначащей информации.
4.1. МЕТОДЫ СЖАТИЯ ДАННЫХ БЕЗ ПОТЕРЬ ИНФОРМАЦИИ.
4.1.1. ОТСУТСТВИЕ СЖАТИЯ ДАННЫХ. ФОРМАТ BMP.
Формат BMP не использует сжатия данных. Структура файла для случая 256-цветных изображений (см. рис. 39 и Табл. 4).
Рис. 39. Общая структура BMP-файла
Таблица 4.
Формат заголовка BMP-файла
Смещение в заголовке |
Длина |
Содержимое |
+0 |
1 |
Буква ‘B’ |
+1 |
1 |
Буква ‘M’ |
29

Климентьев К.Е. Компьютерная графика (курс лекций).
+3 |
4 |
Полный размер файла |
+7 |
2 |
0 |
+9 |
2 |
0 |
+11 |
4 |
Начало изображения в файле |
+15 |
4 |
Размер заголовка (число 40h) |
+33 |
1 |
0 – несжатое изображение; ≠0 – иначе |
Описания точек изображения хранятся в виде 4-х последовательных байтов: R, G, B, 0. Левая верхняя точка изображения хранится в конце файла, следующая точка – в 4-х предыдущих байтах, и т.п., то-есть изображение хранится в перевернутом виде!
4.1.2. МЕТОД RLE (ГРУППОВОГО КОДИРОВАНИЯ). ФОРМАТ PCX.
RLE – run length encoding (бегущее кодирование длины), в отечественной литературе – “метод группового кодирования” или “метод длин серий”. Идея метода: большие группы одинаковых чисел могут быть закодированы парой (Количество, Число). Коэффициент сжатия сильно зависит от количества повторяющихся элементов в сжимаемых данных. Основная проблема – как закодировать сжатые данные, чтобы при обратном раскодировании отличить несжатые данные от ”служебных” записей вида (Количество, Число). Для этого в формате PCX:
•данные кодируются побайтно;
•для индикации о счетчике количества повторов и о начале “служебной” информации используются 2 старших бита, они в этом случае равны 11;
•байт несжатой информации со сброшенными старшими битами сохраняется неизменным;
•байт несжатой информации с установленными старшими битами кодируется в виде пары
(1, Число).
Пример: до сжатия 10h, C0h, C0h, C0h, C0h, C0h, 10h, C0h; после сжатия 10h, С5h, С0h, 10h, C1h, C0h. Коэффициент сжатия равен 8/6 = 1.33.
Особенности формата PCX:
•высокая скорость обработки;
•предельный Ксж = 32;
•“хорошие” коэффициенты сжатия получаются для рисунков типа cartoon;
•при “неудачных” исходных данных вместо сжатия может произойти увеличение объема
данных.
Формат PCX-файла (см. рис. 40 и таблицу 5).
Рис. 40. Формат PCX-файла
Таблица 5
Формат заголовка PCX-файла
Смещение в заголовке |
Длина |
Содержимое |
+0 |
1 |
Код графического редактора |
30
