
Алгоритм умножения матрицы на вектор
Алгоритм
умножения матрицы ![]() (для простоты
возьмем квадратную матрицу) размерности
(для простоты
возьмем квадратную матрицу) размерности
![]() на вектор
на вектор
![]() размерности
размерности
![]() можно
представить как
можно
представить как ![]() скалярных
умножений векторов, получающихся из
строк матрицы
скалярных
умножений векторов, получающихся из
строк матрицы ![]() на вектор
на вектор
![]() . Если строки
матрицы
. Если строки
матрицы ![]() слоистым
образом распределены по процессорам
и вектор
слоистым
образом распределены по процессорам
и вектор ![]() хранится
на каждом процессоре, то параллельный
алгоритм можно записать следующим
образом:
хранится
на каждом процессоре, то параллельный
алгоритм можно записать следующим
образом:
Шаг
1: ![]() на
на ![]()
Шаг
2: ![]() на
на ![]()
Шаг
3: ![]()
На
втором шаге на каждом процессоре
параллельно вычисляются соответствующие
блоки результирующего вектора ![]() , затем (если
это необходимо) на третьем шаге они
пересылаются на первый процессор.
, затем (если
это необходимо) на третьем шаге они
пересылаются на первый процессор.
Предположим,
что столбцы матрицы ![]() распределены
слоистым образом по процессорам. В
этом случае необходимо модифицировать
алгоритм с учетом хранения матрицы.
Результат матрично-векторного
произведения можно получить, умножив
каждый столбец матрицы
распределены
слоистым образом по процессорам. В
этом случае необходимо модифицировать
алгоритм с учетом хранения матрицы.
Результат матрично-векторного
произведения можно получить, умножив
каждый столбец матрицы ![]() на
соответствующий элемент вектора
на
соответствующий элемент вектора ![]() и сложив
получившиеся вектора. Степень параллелизма
этого алгоритма меньше, чем в предыдущем,
и обусловлена тем, что приходится
осуществлять суммирование.
и сложив
получившиеся вектора. Степень параллелизма
этого алгоритма меньше, чем в предыдущем,
и обусловлена тем, что приходится
осуществлять суммирование.
Условно, по шагам алгоритм записывается следующим образом:
Шаг
1: ![]() на
на ![]()
Шаг
2: ![]() на
на ![]()
Шаг
3: ![]() на
на ![]()
Шаг
4: ![]()
Шаг
5: ![]() на
на ![]()
На втором шаге осуществляется покомпонентное умножение векторов, на третьем – частичное суммирование, на четвертом – пересылка частичных сумм на первый процессор, на последнем – завершающее суммирование.
Матрично-векторное
умножение обычно является частью более
широкого процесса вычислений и для
выбора того или иного алгоритма главную
роль играет способ хранения ![]() и
и ![]() в момент,
когда требуется их произведение.
Например, если
в момент,
когда требуется их произведение.
Например, если ![]() и
и ![]() уже находятся
в памяти
уже находятся
в памяти ![]() -го процессора,
то эффективнее использовать второй
алгоритм, хотя степень параллелизма в
нем ниже, чем в первом. Еще один важный
фактор при выборе параллельного
алгоритма - желаемое расположение
результата по окончании операции
умножения: во втором алгоритме
вектор-результат размещается в памяти
одного процессора, тогда как в первом
он распределен по процессорам.
-го процессора,
то эффективнее использовать второй
алгоритм, хотя степень параллелизма в
нем ниже, чем в первом. Еще один важный
фактор при выборе параллельного
алгоритма - желаемое расположение
результата по окончании операции
умножения: во втором алгоритме
вектор-результат размещается в памяти
одного процессора, тогда как в первом
он распределен по процессорам.
program EXAMPLE
include 'mpif.h'
integer my_id, np, comm, tag, count, ierr, n,q
integer i,j,k
integer a(100,100),b(100)
integer c(100,100),a1(100,100),a2(100,100)
integer status(MPI_STATUS_SIZE)
double precision t1,tfinish
call MPI_Init(ierr)
comm=MPI_COMM_WORLD
call MPI_Comm_rank(COMM, my_id, ierr)
call MPI_Comm_size(COMM, np, ierr)
print *, 'Process ', my_id, ' of ', np, ' is alive'
! Инициализация матриц
t1=MPI_Wtime()
call MPI_Bcast(n,1,MPI_INTEGER,0,COMM,ierr)
call MPI_Bcast(b,n,MPI_INTEGER,0,COMM,ierr)
call MPI_Scatter(a,int(n*n/np),MPI_INTEGER,a1,
* int(n*n/np),MPI_INTEGER,0,COMM,ierr)
c=0
do j=1,n,1
do i=1,int(n/np),1
do k=1,n,1
c(i+int(n/np)*my_id,j)=
*c(i+int(n/np)*my_id,j)+a1(k,i)*b(k)
end do
end do
end do
call MPI_Reduce(c,a2,n*n,MPI_INTEGER,MPI_SUM,
*0, COMM,ierr)
t1=MPI_Wtime()-t1
write(*,*) 'Dim = ',n,' the time is ',t1
call MPI_Finalize(ierr)
stop
end
Задание: Алгоритм умножения матриц
Реализовать любой вариант параллельного умножения матриц.
Пример:
Приведенные параллельные алгоритмы матрично-векторного произведения естественным образом обобщаются на задачу умножения матриц. Приведенные же ниже алгоритмы будут обсуждаться с точки зрения того, как хранились матрицы до операции произведения и после нее.
Для
простоты возьмем квадратные матрицы
![]() и
и ![]() размерности
размерности
![]() .
.
Первый
вариант параллельного алгоритма
матричного умножения будем строить,
предполагая, что матрица ![]() распределена
по процессорам слоистым образом по
строкам, а матрица
распределена
по процессорам слоистым образом по
строкам, а матрица ![]() - целиком.
В этом случае искомый результат можно
получить, выполнив параллельно на
каждом процессоре
- целиком.
В этом случае искомый результат можно
получить, выполнив параллельно на
каждом процессоре ![]() скалярных
произведений.
скалярных
произведений.
Приведем алгоритм:
Шаг
1: ![]() на
на ![]()
Шаг
2: 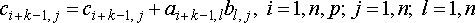 на
на  (причем
циклы по индексам расположены в следующей
последовательности
(причем
циклы по индексам расположены в следующей
последовательности ![]()
Шаг
3: 
Второй
вариант параллельного алгоритма
матричного умножения будем строить,
предполагая, что матрица  распределена
по процессорам слоистым образом по
столбцам, а матрица
распределена
по процессорам слоистым образом по
столбцам, а матрица ![]() - целиком.
В этом случае искомый результат можно
получить, выполнив параллельно на
каждом процессоре умножение соответствующих
столбцов матрицы
- целиком.
В этом случае искомый результат можно
получить, выполнив параллельно на
каждом процессоре умножение соответствующих
столбцов матрицы  на
соответствующие элементы строк матрицы
на
соответствующие элементы строк матрицы
 , затем
необходимо осуществить частичное
суммирование получившихся произведений
и на последнем шаге, переслав матрицы
с частичными суммами на один процессор,
закончить суммирование. Алгоритм
опустим ввиду его громоздкости и
очевидности.
, затем
необходимо осуществить частичное
суммирование получившихся произведений
и на последнем шаге, переслав матрицы
с частичными суммами на один процессор,
закончить суммирование. Алгоритм
опустим ввиду его громоздкости и
очевидности.
Возможные
способы хранения исходных матриц
порождают другие алгоритмы. Например,
матрица  распределена
по процессорам слоистым образом по
строкам, а матрица
распределена
по процессорам слоистым образом по
строкам, а матрица  - целиком,
или
- целиком,
или  распределена
по процессорам слоистым образом по
столбцам, а
распределена
по процессорам слоистым образом по
столбцам, а  - целиком.
Алгоритмы при этом схожи с рассмотренными
выше.
- целиком.
Алгоритмы при этом схожи с рассмотренными
выше.
Возможно
также построение алгоритмов, которые
основаны на блочном распределении
матриц  и
и  по процессорам.
по процессорам.
Если разбиения обеих матриц на блоки согласованы, то
 ,
,
где
 или
или 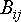 - миноры
соответствующих матриц. Это представление
можно реализовать разными алгоритмами.
Пусть, например, число процессоров
- миноры
соответствующих матриц. Это представление
можно реализовать разными алгоритмами.
Пусть, например, число процессоров  равно
равно  (числу
миноров матрицы
(числу
миноров матрицы  . При условии,
что матрицы
. При условии,
что матрицы  и
и  распределены
соответствующим образом по процессорам,
все миноры матрицы
распределены
соответствующим образом по процессорам,
все миноры матрицы  можно
вычислять одновременно.
можно
вычислять одновременно.
