
Классич вер 4
.doc§4. ВЕРОЯТНОСТЬ СЛУЧАЙНОГО СОБЫТИЯ
На дне глубокого сосуда
Лежат спокойно n шаров,
Поочередно их оттуда
Таскают двое дураков.
Сие занятье им приятно,
Они таскают m минут
И, взявши шар, его обратно
В сосуд немедленно кладут.
Ввиду условия такого
Сколь вероятность велика,
Что первый был глупей второго,
Когда шаров он вынул k?
Вероятность события численно характеризует степень возможности его появления в рассматриваемом опыте.
Пусть производится эксперимент с n равновозможными элементарными исходами, образующими полную группу несовместных событий.
Определение 4.1 (классическое). Вероятностью события А называется отношение числа m исходов, благоприятствующих этому событию, к общему числу n исходов:
![]() .
.
Вероятность обладает следующими свойствами:
-
0
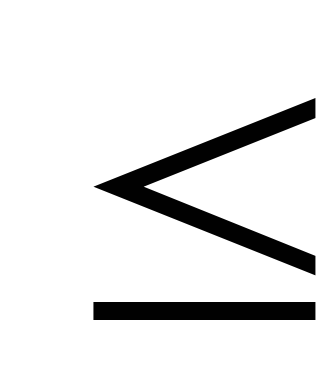 P(A)
P(A)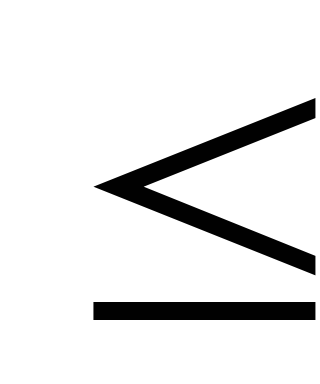 1
для
любого события А;
1
для
любого события А; -
P(∅)=0;
-
P(
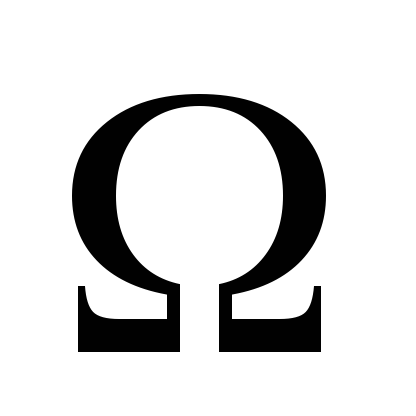 )=1;
)=1; -
Р(А)+P(
 )=1
для любого события А;
)=1
для любого события А; -
P(A+B)=P(A)+P(B), если А∙В=∅;
-
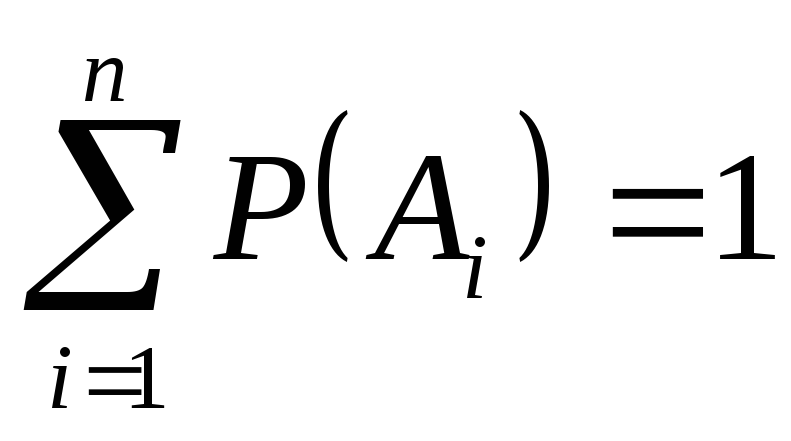 ,
если
,
если
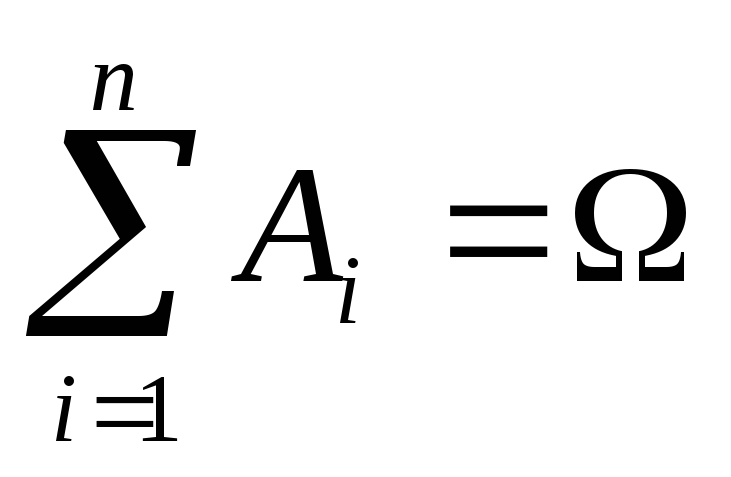 и Ai∙Aj=∅
(i
и Ai∙Aj=∅
(i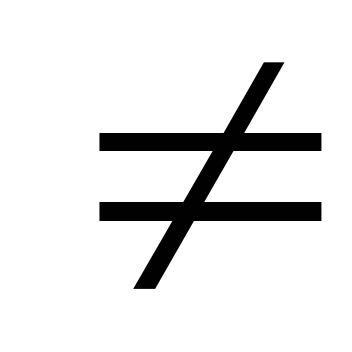 j).
j).
Пример 4.1. Клоун жонглирует 3 красными, 1 зеленым и 2 синими шариками. Какова вероятность, что случайно оброненный им шарик не будет синим?
Решение.
В данном случае мы рассматриваем
эксперимент с 6 равновозможными
элементарными исходами (шариков всего
шесть). Исходов, благоприятствующих
событию «оброненный шарик не является
синим», – четыре (3 красных и 1 зеленый
шарик). Т.о. искомая вероятность равна
![]() или
или
![]() .
Заметим, что задачу можно решить и другим
способом: вычислить вероятность
противоположного события «упавший
шарик – синего цвета» и вычесть ее из
единицы. Получим тот же ответ: 1–
.
Заметим, что задачу можно решить и другим
способом: вычислить вероятность
противоположного события «упавший
шарик – синего цвета» и вычесть ее из
единицы. Получим тот же ответ: 1–![]() =
=![]() .
.
Обобщением понятия «классической вероятности» на случай опытов с бесконечным (вообще говоря, несчетным) числом исходов является понятие «геометрической вероятности». К этому понятию приводят задачи на подсчет вероятности попадания точки в некую область (отрезок, часть плоскости, часть пространства и т.д.).
Пусть
пространство элементарных событий
![]() представляет собой некоторую область
плоскости. Тогда в качестве событий
могут рассматриваться области А,
содержащиеся
в
представляет собой некоторую область
плоскости. Тогда в качестве событий
могут рассматриваться области А,
содержащиеся
в
![]() .
.
Определение
4.2 (геометрическое). Вероятность
попадания в область А
точки,
наудачу выбранной из области
![]() ,
называется
геометрической
вероятностью
события
А
и
находится по формуле
,
называется
геометрической
вероятностью
события
А
и
находится по формуле
![]() ,
,
где
S(A)
и
S(![]() )
– площади
областей А
и
)
– площади
областей А
и
![]() соответственно.
соответственно.
Случай,
когда
![]() представляет
собой отрезок или трехмерную область,
рассматривается аналогично.
представляет
собой отрезок или трехмерную область,
рассматривается аналогично.
Пример 4.2. Престарелая тетушка раскладывает пасьянс. Она делит полную колоду карт (52 штуки) наугад на две равные пачки по 26 листов. Найдите вероятности следующих событий:
А – в каждой из пачек окажется по два туза;
В – в одной из пачек не будет ни одного туза;
С – в одной из пачек будет один туз, а в другой три.
Решение.
Общее число случаев n=![]() – число способов выбрать из всей колоды
26 карт, остальные окажутся во второй
пачке. Число случаев, благоприятствующих
событию А, есть m=
– число способов выбрать из всей колоды
26 карт, остальные окажутся во второй
пачке. Число случаев, благоприятствующих
событию А, есть m=![]() –
–
![]() вариантов выбора двух тузов из четырех,
каждому из которых соответствует
вариантов выбора двух тузов из четырех,
каждому из которых соответствует
![]() вариантов выбрать остальные карты в
пачке. В этом случае
вариантов выбрать остальные карты в
пачке. В этом случае
 .
Событие В может осуществиться двумя
способами: либо в первой пачке будут
все четыре туза, а во второй – ни одного,
либо наоборот:
.
Событие В может осуществиться двумя
способами: либо в первой пачке будут
все четыре туза, а во второй – ни одного,
либо наоборот:
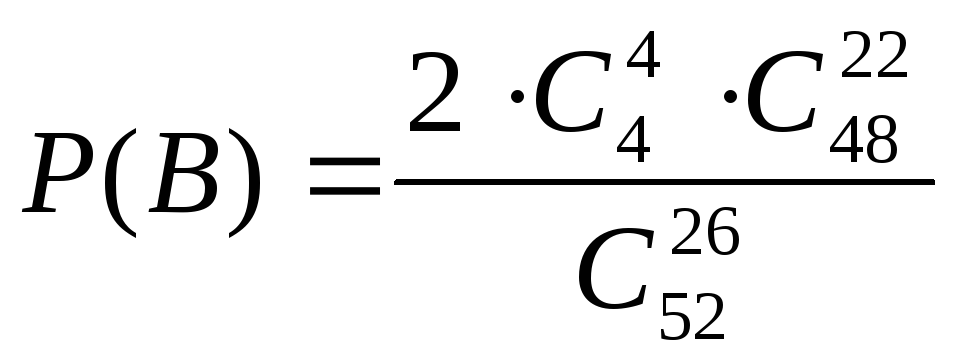 .
Аналогично для события C:
.
Аналогично для события C:
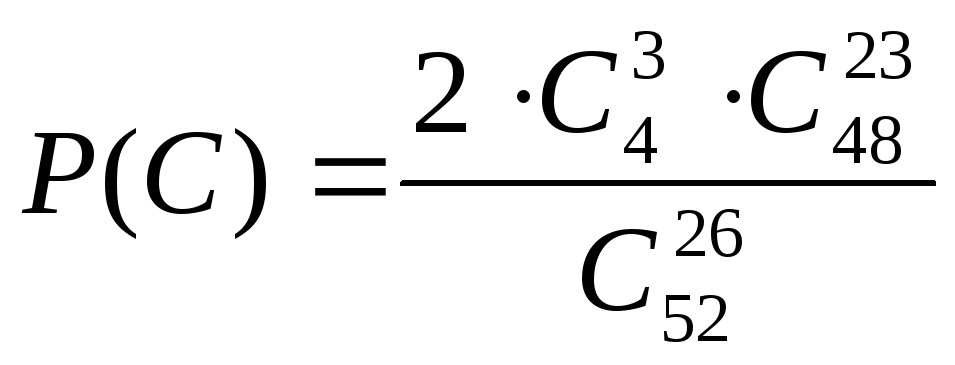 .
.
Пример 4.3. Из букв разрезной азбуки мама составила слово «книга». Ребенок, не умеющий читать, рассыпал эти буквы и затем собрал в произвольном порядке. Найдите вероятность того, что у него снова получилось слово «книга». Решите ту же задачу при условии, что мама составила слово «ананас».
Решение. Все
буквы в слове «книга» различны, поэтому
общее количество слов, которое может
составить ребенок, есть n=P5=5!=120.
Так как лишь одно слово из них верное,
то вероятность события равна
![]() .
В случае со словом «ананас», в котором
есть повторяющиеся буквы «а» и «н»,
вероятность будет равна
.
В случае со словом «ананас», в котором
есть повторяющиеся буквы «а» и «н»,
вероятность будет равна
![]() .
.
Пример 4.4. Какова вероятность того, что корни уравнения x2+px+q=0 будут действительными, если коэффициенты р и q уравнения выбираются наудачу из отрезка [0;1]?
 Решение.
Будем рассматривать множество всех
возможных пар чисел (p;q)
как координаты
точек единичного квадрата с вершинами
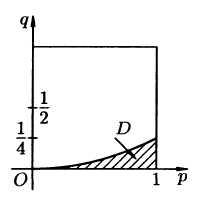
(0;0), (0;1), (1;1), (1;0) (см. рис.4.1). Поэтому
Решение.
Будем рассматривать множество всех
возможных пар чисел (p;q)
как координаты
точек единичного квадрата с вершинами
(0;0), (0;1), (1;1), (1;0) (см. рис.4.1). Поэтому
![]() = {(p;q)
= {(p;q)
![]() 0
0![]() p
p![]() 1,
0
1,
0![]() q
q![]() 1}.
1}.
Корни уравнения действительны, если выполняется
неравенство
p2–4q![]() 0,
т.е. q
0,
т.е. q![]() p2.
Отсюда ясно, что
p2.
Отсюда ясно, что
Рис.4.1
множество точек квадрата, благоприятствующих
событию А
«корни уравнения
действительны», есть
область D
(на рисунке
область D
заштрихована):
D={(p;q)
![]() q
q![]() p2,
0
p2,
0![]() p
p![]() 1,
0
1,
0![]() q
q![]() 1}.
Поэтому искомая вероятность равна
1}.
Поэтому искомая вероятность равна
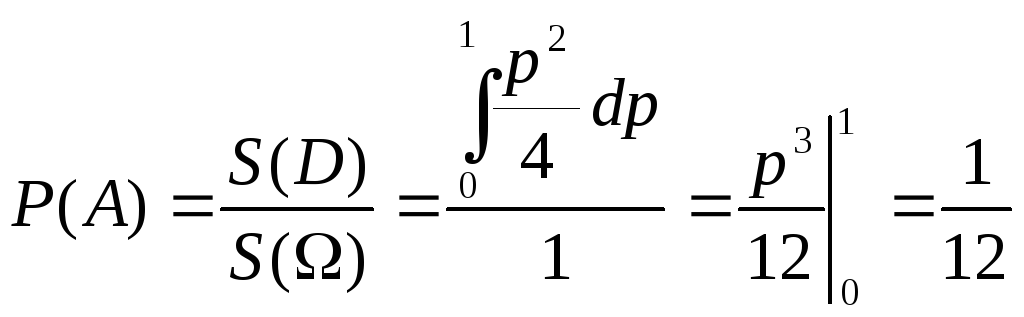 .
.
Решите задачи:
1. В урне а белых и b черных шаров. Из урны вынимают наугад один шар. Найдите вероятность того, что этот шар белый.
2. В урне а белых и b черных шаров. Из урны вынимают один шар и откладывают в сторону. Этот шар оказался белым. После этого из урн берут еще один шар. Найдите вероятность того, что этот шар тоже будет белым.
3. В урне а белых и b черных шаров. Из урны вынули один шар и, не глядя, отложили в сторону. После этого из урны взяли еще один шар. Он оказался белым. Найдите вероятность того, что первый шар, отложенный в сторону, тоже белый.
4. Из урны, содержащей а белых и b черных шаров, вынимают один за другим все шары, кроме одного. Найдите вероятность того, что последний оставшийся в урне шар будет белым.
5. Из урны, в которой а белых шаров и b черных, вынимают подряд все находящиеся в ней шары. Найдите вероятность того, что вторым по порядку будет вынут белый шар.
6.
В урне а
белых
и b
черных
шаров (а![]() 2).
Из урны вынимают сразу два шара. Найдите
вероятность того, что оба шара будут
белыми.
2).
Из урны вынимают сразу два шара. Найдите
вероятность того, что оба шара будут
белыми.
7.
В урне а белых
и b
черных шаров
(a![]() 2,
b
2,
b![]() 3).
Из урны вынимают
сразу пять шаров. Найдите вероятность
того, что два из них будут белыми, а три
черными.
3).
Из урны вынимают
сразу пять шаров. Найдите вероятность
того, что два из них будут белыми, а три
черными.
8.
В урне а белых
и b
черных шаров
(а![]() 2;
b
2;
b![]() 2).
Из урны вынимают
одновременно два шара. Какое событие
более вероятно:
2).
Из урны вынимают
одновременно два шара. Какое событие
более вероятно:
А – шары одного цвета; В – шары разных цветов?
9. В урне а белых, b черных и с красных шаров. Из урны вынимают один за другим все находящиеся в ней шары и записывают их цвета. Найдите вероятность того, что в этом списке белый цвет появится раньше черного.
10.
В урне имеется
k
шаров, помеченных
номерами 1, 2, ..., k.
Из урны n
раз вынимается по одному шару (n![]() k),
номер шара записывается и шар кладется
обратно в урну. Найдите вероятность
того, что все записанные номера будут
различны.
k),
номер шара записывается и шар кладется
обратно в урну. Найдите вероятность
того, что все записанные номера будут
различны.
11. Игральная кость бросается один раз. Найдите вероятность следующих событий:
А – появление 5 очков;
В – появление не менее 5 очков;
С – появление не более 5 очков;
D – появление числа очков, кратного 3;
E – появление четного числа очков;
F – появление числа очков, большего 2.
12. Игральная кость бросается два раза. Найдите вероятность следующих событий:
А – оба раза появилось одинаковое число очков;
В – число очков при первом бросании больше, чем при втором;
С – сумма очков четна;
D – сумма очков больше 2;
E – сумма очков не меньше 5;
F – хотя бы один раз выпало число 6;
G – произведение очков равно 6.
13. В розыгрыше первенства по баскетболу участвуют 18 команд, из которых случайным образом формируются две группы по 9 команд в каждой. Среди участников соревнований имеется 5 команд экстра-класса. Найдите вероятности следующих событий:
А – все команды экстра-класса попадут в одну и ту же группу;
В – две команды экстра-класса попадут в одну группу, а три в другую.
14. В группе из k студентов, имеется m отличников. Наудачу для интернет-тестирования выбирают n студентов группы. Найдите вероятность того, что из них ровно s студентов окажутся отличниками.
15. Железнодорожный состав из 9 вагонов и вагона-ресторана формируется произвольным образом. Найдите вероятность того, что:
а) вагон №7 и вагон-ресторан расположены рядом;
б) между вагоном №7 и вагоном-рестораном окажется пять вагонов.
16. N рыцарей случайным образом рассаживаются за круглым столом (N>2). Найдите вероятность того, что сэр Ланселот и сэр Мордред окажутся рядом. Решите ту же задачу при условии, что стол прямоугольный, и N рыцарей рассаживаются случайно вдоль одной из его сторон.
17. В лифт семиэтажного дома на первом этаже вошли три человека, не знакомых друг с другом. Каждый из них с одинаковой вероятностью выходит на любом из этажей, начиная со второго. Найдите вероятности следующих событий:
А – все пассажиры выйдут на четвертом этаже;
В – все пассажиры выйдут одновременно (на одном и том же этаже);
С – все пассажиры выйдут на разных этажах.
18. Составляя подарок для послушного ребенка, Дед Мороз наугад выбирает 3 игрушки из 5 имеющихся видов. Найдите вероятность того, что все игрушки в подарке будут различны.
19. Калиф-Аист забыл волшебное слово «мутабор» и произносит слова наудачу. Он помнит длину заветного слова. Найдите вероятности следующих событий:
А – он угадает, если помнит все буквы слова;
В – он угадает, если помнит, что в слове не было никаких букв, кроме «м», «у», «т», «а», «б», «о», «р» (входили ли эти буквы в слово и по сколько раз, он не помнит);
С – Калиф произнесет слово, в котором будет сочетание букв «табу», если он помнит все входящие в слово буквы?
20. Наудачу выбирают неотрицательное число, не превосходящее трех. Какова вероятность того, что это число не меньше единицы?
21.
Наудачу выбирают вещественные числа x
и y так, что x![]() [0;2],
y
[0;2],
y![]() [0;1].
Какова вероятность следующих событий:
[0;1].
Какова вероятность следующих событий:
1)
x![]()
![]() и
y
и
y![]() ;
2)
y
;
2)
y![]() 2x;
3)
y
2x;
3)
y![]() sinx.
sinx.
22. Двенадцатиметровый стержень сломали в произвольной точке. Найдите вероятность того, что меньший из обломков имеет длину, превышающую 2 м.
23. На пол, покрытый кафельной плиткой со стороной 5 см, случайно падает монета радиуса 1 см. Найдите вероятность того, что монета целиком окажется внутри квадратной плитки.
24. Мальчик учится играть в дартс, бросая дротик в мишень из двух концентрических окружностей с радиусами 10 и 20 см. Найдите вероятность того, что брошенный в мишень дротик попадет в кольцо, образованное этими окружностями.
