5. Подбор подходящего распределения к опытным данным.

Полученные экспериментальные данные при достаточно большом объеме выборки позволяют подобрать подходящее распределение вероятностей. С этой целью можно воспользоваться перебором известных распределений.

Предположим, что случайная величина X имеет распределение вероятностей (нормальное, экспоненциальное и т.д.) с функцией распределения F(x). Будем называть это предположение гипотезой о виде распределения случайной величины X. Однако, чтобы иметь полную информацию о распределении случайной величины, надо еще знать параметры этого распределения или их некоторые оценки. Исторически одним из первых методов для оценивания неизвестных параметров является метод моментов, согласно которому параметры распределений берутся такими, чтобы выборочные моменты были бы равны соответствующим моментам распределения случайной величины X. Например, нормальное распределение имеет два неизвестных параметра a и  (см прил.1), которые заменяются на соответствующие выборочные характеристики иs. Экспоненциальное распределение имеет один неизвестный параметр , равный величине обратной математическому ожиданию, и поэтому согласно методу моментов .

Возникает вопрос: насколько наша гипотеза о распределении случайной величины X соответствует экспериментальным данным? Для решения этой задачи разработаны критерии согласия, из которых наиболее распространенными являются критерий ² (или критерий Пирсона) и критерий Колмогорова-Смирнова.

Мы рассмотрим здесь лишь критерий ². Для его применения необходимо, чтобы частоты n_i, соответствующие каждому интервалу, были бы не меньше 5. Если это не так, рядом стоящие интервалы объединяются, а их частоты суммируются. В результате общее количество интервалов может уменьшиться до значения k^. Далее вычисляется следующая сумма

,

где p_i - теоретическая вероятность того, что случайная величина X примет значение из интервала [a_i-1,a_i]. Мы предположили, что случайная величина X имеет функцию распределения F(x), поэтому p_i=F(a_i)-F(a_i-1). Величина показывает меру близости относительных частоти вероятностейp_i.

Гипотеза о виде закона распределения должна быть принята, если вычисленное значение достаточно мало, а именно, оно не превосходит критического значения, которое можно взять из таблиц распределения² в зависимости от заданного уровня значимости  (вероятность того, что будет опровергнута правильная гипотеза) и числа степеней свободы r=k-s-1. Здесь s - число неизвестных параметров распределения, которые были определены по выборке (для нормального распределения s=2, для экспоненциального распределения s=1 и т.п.).

На практике часто поступают иначе, а именно, по вычисленному значению находят соответствующее значение уровня значимости

,

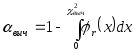где - плотность² распределения с r степенями свободы. Если окажется, что вероятность превышает заданный уровень значимости, то есть , то нет оснований отвергнуть гипотезу о виде распределения. Если, то гипотеза о виде распределения не согласуется с данными эксперимента. В этом случае надо предположить, что случайная величинаX имеет какой-либо другой закон распределения, а затем аналогичным образом принять или опровергнуть эту гипотезу.

Приложение.

Список дискретных и непрерывных распределений.

В табл.П1 приведен перечень дискретных и непрерывных распределений, содержащихся в пакете StatGraphics. Указано также количество и название параметров каждого распределения.

Таблица П1

Номер Распред.	Распределение	Кол-во парам.	Параметры
Дискретные распределения
1	Бернулли	1	вероятность успеха
2	Биномиальное	2	число опытов, вероятность появления события
3	Дискретное равномерное	2	нижний предел, верхний предел
4	Геометрическое	1	вероятность появления события
5	Отрицательное биномиальное	2	количество успехов, вероятность наступления события
6	Пуассона	1	среднее значение
Непрерывные распределения
7	Бета	2	, 
8	Хи-квадрат	1	число степеней свободы
9	Эрланга	2	формы (), масштаба ()
10	Экспоненциальное	1	среднее значение
11	Фишера	2	число степеней свободы числителя, число степеней свободы знаменателя
12	Гамма		формы (), масштаба ()
13	Логнормальное	2	среднее значение, стандартное отклонение
14	Нормальное	2	среднее значение, стандартное отклонение
15	Стьюдента	1	число степеней свободы
16	Треугольное	3	нижний предел, центральный предел, верхний предел
17	Равномерное	2	нижний предел, верхний предел
18	Вейбулла	2	формы (), масштаба ()