Элементы математического программирования

Задача 37. Построить на плоскости область решений системы линейных неравенств и геометрически найти наименьшее и наибольшее значения линейной функции.

37.1. 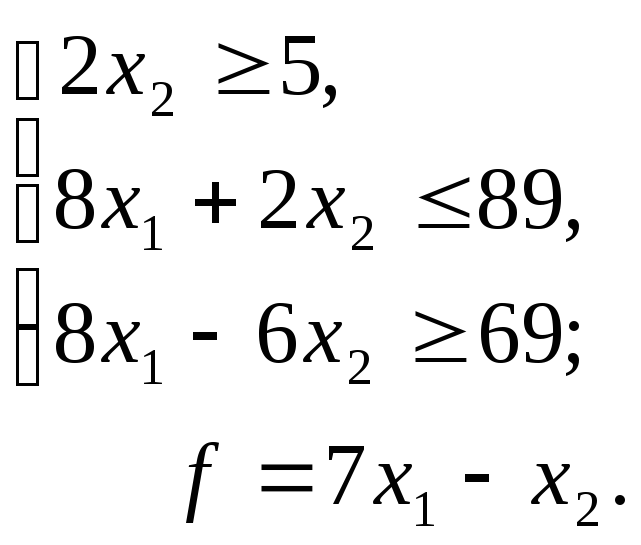37.2.

37.3. 37.4.

37.5. 37.6.

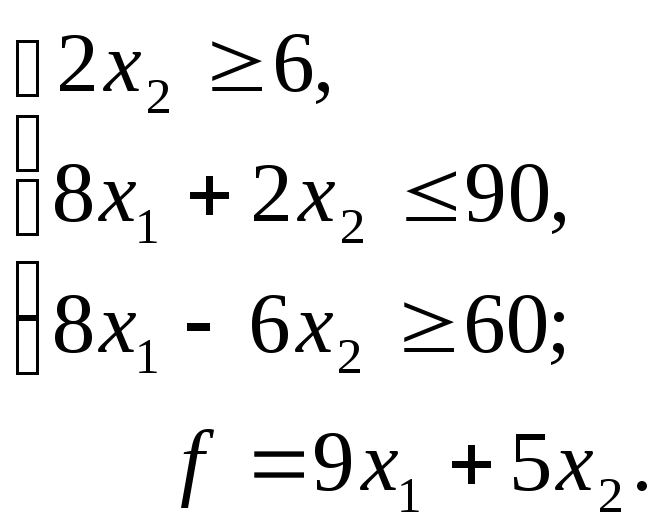
37.7. 37.8.

37.9. 37.10

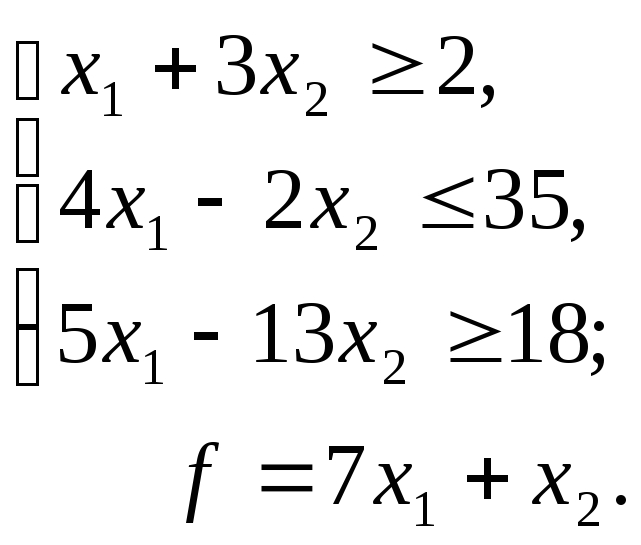
Задача 38. Предположим, что для производства двух видов продукции А и В можно использовать материал только трех сортов. При этом на изготовление единицы изделия вида А расходуется кг материала первого сорта,кг материала второго сорта икг материала третьего сорта. На изготовление единицы изделия видарасходуетсякг материала первого сорта,кг материала второго сорта,кг материала третьего сорта. На складе фабрики имеется всего материала первого сортакг, материала второго сортакг, материала третьего сортакг. От реализации единицы готовой продукции видаА фабрика имеет прибыль руб., продукции видаВ прибыль составляет руб.

Определить максимальную прибыль от реализации всей продукции видов А и В. Решить задачу симплекс-методом. Дать геометрическую интерпретацию математической формулировки задачи.

38.1.

2. 

38.3.

38.4.

38.5.

38.6.

38.7.

38.8.

38.9.

38.10.

Задача 39. Имеются три пункта поставки однородного груза пять пунктов потребления этого груза. На пунктах находится груз соответственно в количестве т. В пунктытребуется доставить соответственнот груза.

Расстояние между пунктами потребления приведено в следующей матрице таблице:

Пункты поставки	Пункты потребления

Найти такой план закрепления потребителей за поставщиками однородного груза, чтобы общие затраты по перевозкам были минимальными.

39.1.

39.2.

39.3.

39.4.

39.5.

39.6.

39.7.

39.8.

39.9.

39.10.

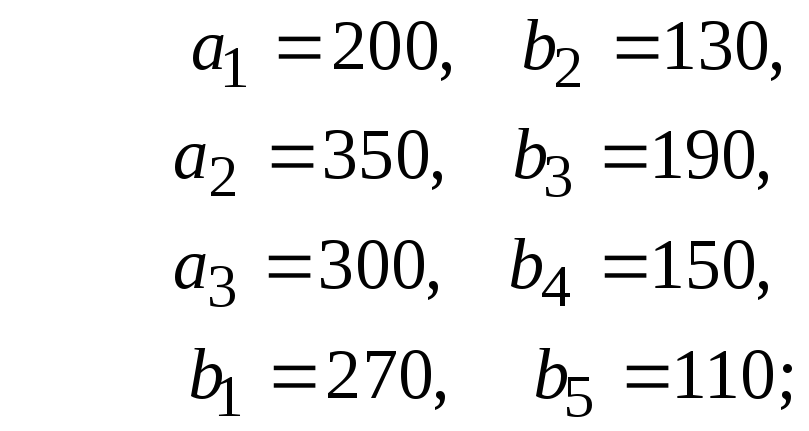
Решения типовых задач

Задача 1. Даны векторы , , и в некотором базисе трехмерного пространства. Показать, что векторы образуют базис данного трехмерного пространства и найти координаты вектора в этом базисе.

Решение. Векторы образуют базис, если они линейно независимы. Составим векторное равенство . Записывая в виде векторов – столбцов, получим . Задача свелась, таким образом, к решению системы . Решим систему методом Гаусса. . Итак, система приведена к виду . Полученная система имеет единственное нулевое решение:, т.е. векторы линейно независимы и, следовательно, составляют базис. Вектор можно представить в виде , т.е. координаты вектора в этом базисе . Для отыскания координат вектора решим систему линейных уравнений методом Гаусса: .

.

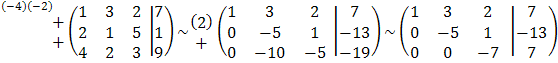Итак, система приведена к виду .

Находим . т.е. вектор .

Задача 2. Даны векторы , , , и . Показать, что векторы образуют базис четырехмерного пространства, и найти координаты вектора в этом базисе.

Решение. Векторы образуют базис, если они линейно независимы. Составим векторное равенство . Записывая в виде векторов – столбцов, получим .

Задача свелась, таким образом, к решению системы

Решим систему методом Гаусса.

. Итак, система приведена к виду .

Полученная система имеет единственное нулевое решение: , т.е. векторы линейно независимы и, следовательно, составляют базис. Вектор можно представить в виде , т.е. координаты вектора в этом базисе . Для отыскания координат вектора решим систему линейных уравнений методом Гаусса: .

.

Итак, система приведена к виду .

Находим , т.е. вектор .

Задача 3. Даны вершины треугольника :. Найти: 1) длину стороны; 2) внутренний уголв радианах с точностью до 0,001; 3) уравнение высоты, проведенной через вершину; 4) уравнение медианы, проведенной через вершину; 5) точку пересечения высот треугольника; 6) длину высоты, опущенной из вершины; 7) систему неравенств, определяющих треугольник

Решение.

1) Длину стороны (длина вектора) находим как расстояние между двумя точками плоскостии:.

Поэтому

2) Угол – это угол между векторамии. Координаты этих векторов:,. Таким образом.

Таким образом, получаем

3) Составим уравнение стороны :, или. Угловой коэффициент стороныравен; следовательно, в силу условия перпендикулярности, угловой коэффициент высоты, проведенной из вершины, равен. Уравнение этой высоты имеет вид, получаем, или.

4) Пусть точка М середина стороны . Найдем ее координаты:

т..

Уравнение медианы находим с помощью уравнения прямой, проходящей через две данные точки:, получим.

5) Составим уравнение еще одной высоты треугольника . Например, выберем высоту, проведенную из вершины. Аналогично пункту 3) составим уравнение стороны:

.

Угловой коэффициент стороны равен; следовательно, в силу условия перпендикулярности, угловой коэффициент высоты, проведенной из вершины, равен. Уравнение этой высоты имеет вид, получаем, или. Поскольку мы ищем точку пересечения высот треугольника, то координаты этой точки должны удовлетворять системе уравнений;. Таким образом точка пересечения высот треугольникаимеет координаты

6) Найдем длину высоты, опущенной из вершины по формуле расстояния от точкидо прямой::. Таким образом

7) Стороны треугольника заданы уравнениями прямых:

: ; (см. пункт 3).

: ; (см. пункт 5).

: ;;.

Каждая из этих прямых делит координатную плоскость на две полуплоскости. Область треугольника лежит выше прямой, т.е. в полуплоскости, которая задается неравенством:. Прямаяделит координатную плоскость на две полуплоскости, нам необходима та, которая удовлетворяет неравенству:. Из двух полуплоскостей, которые разделяет прямая, выбираем ту, которая задается неравенством:.

Таким образом, область треугольника , определяется системой неравенств:

Задача 4. Даны координаты вершин пирамиды :

. Найти:

1. длину ребра ;

2. угол между ребрами и ;

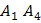3. угол между ребром и гранью ;

4. площадь грани ;

5. объем пирамиды; 6) уравнение прямой ;

7) уравнение плоскости ;

8) уравнение высоты, опущенной из вершины на грань . Сделать чертеж.

Р

ешение.

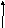
𝛽

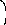
,𝐴-₂.

1. Длина ребра есть длина вектора , координаты которого Т.к. длина вектора находится по формуле , то .

2. Угол между ребрами и есть угол между векторами

=(-1,5,1) и =(4-6;4-1;10-1)=(-2;3;9), поэтому

Отсюда

3. Обозначим угол между ребром и гранью через , тогда , где – угол между вектором =(-2;3;9) и нормальным вектором плоскости , которым является, например, векторное произведение векторов и

Т.к. векторное произведение векторов =() и находится по формуле , то . Итак, . Найдем теперь угол

значит

или

4) Т.к. длина векторного произведения двух векторов равна площади параллелограмма, построенного на этих векторах, как на сторонах, то площадь S грани (площадь треугольника) найдем как половину площади параллелограмма, построенного на векторах и как на сторонах, т.е. как половину длины векторного произведения этих векторов.

Т.к. (см. пункт 3), то

5) Т.к. объем V треугольной пирамиды, построенной на векторах , находится по формуле , где - смешанное произведение векторов , то

. Найдем смешанное произведение векторов

и по формуле

:

(определитель вычислен по схеме треугольников). Итак, .

6) Т.к. уравнение прямой, проходящей через точку параллельно вектору имеет вид , то уравнение прямой найдем как уравнение прямой, проходящей через точку в направлении вектора : .

7) Т.к. уравнение плоскости, проходящей через точку перпендикулярно вектору имеет вид ( нормальный вектор плоскости), то уравнение плоскости найдем как уравнение плоскости, проходящей через точку с нормальным вектором (см. пункт 3):

или

8) Уравнение высоты, опущенной из вершины на грань , найдем как уравнение прямой, проходящей через точку в направлении вектора -нормального вектора плоскости (см. пункт 3): .

Задача 5. Найти матрицу, обратную матрице . Проверить результат, вычислив произведение данной и обратной матриц.

Решение. Определитель матрицы

, значит обратная матрица существует. Найдем матрицу , транспонированную к : . Найдем алгебраические дополнения всех элементов матрицы и составим из них присоединенную матрицу .

.

Найдем обратную матрицу :

.

Проверка:

.

.

Задача 6. Дана система линейных уравнений

Доказать её совместность и решить двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления.

Решение. 1) Докажем совместность системы. Для этого вычислим ранг матрицы А исходной системы и ранг расширенной матрицы системы

Для удобства вычислений элементарные преобразования будем производить с матрицей :

2

3

~ ~~

т.е. по теореме Кронекера–Капелли система совместна.

2) Решим систему методом Гаусса. Для этого матрицу приведем к диагональному виду:

тиии

3) Решим систему матричным способом. Для этого введем следующие матрицы и исходную систему запишем в матричном виде.

.

Вычислим обратную матрицу . Определитель матрицыА , значит обратная матрица существует. Затем, вычислив к каждому элементу матрицыА алгебраические дополнения, составим из них матрицу , транспонируем ееи находим обратную матрицу.

=.

Ответ:

Задача 7. Найти пределы функций, не пользуясь правилом Лопиталя.

а) ; б) ; в) ; г) .

Решение. а) Для раскрытия неопределенности разделим числитель и знаменатель дроби на высшую степень (на ):

. Здесь учитывалось стремление к нулю дробей как обратных к бесконечно большим функциям.

б) Для раскрытия неопределенности умножим и разделим на выражение, сопряженное числителю, т.е. на :

=

.

Использовалась формула .

в) Для раскрытия неопределенности воспользуемся эквивалентностями (следствиями первого замечательного предела): и при и тем, что при вычислении предела частного можно одну бесконечно малую величину заменить на ей эквивалентную в этом процессе:

.

г) Для раскрытия неопределенности преобразуем выражение, чтобы воспользоваться следствием второго замечательного предела:

.

=

.

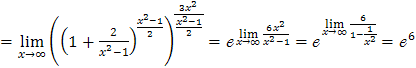Здесь бесконечно малой величиной является выражение .

Задача 8. Найти пределы функций, не пользуясь правилом Лопиталя.

1) при а) ; б) ; в) ;

2) ; 3) ; 4) .

Решение. 1) а) .

б) Для раскрытия неопределенности разложим числитель и знаменатель на множители:

.

в) Для раскрытия неопределенности разделим числитель и знаменатель дроби на высшую степень (на ):

. Здесь учитывалось стремление к нулю дробей , как обратных к бесконечно большим функциям.

2) Для раскрытия неопределенности умножим и разделим на выражение, сопряженное знаменателю до разности квадратов

, т.е. на :

=

3) Для раскрытия неопределенности воспользуемся эквивалентностями (следствиями первого замечательного предела): и при и тем, что при вычислении предела частного можно одну бесконечно малую величину заменить на ей эквивалентную в этом процессе:

.

4) Для раскрытия неопределенности преобразуем выражение, чтобы воспользоваться следствием второго замечательного предела:

.

Здесь бесконечно малой величиной является выражение .

Задача 9. Найти точки разрыва функции

Решение. Так как у данной функции нет точек, в которых она неопределенна, то точками разрыва могут быть либо нули знаменателя, либо точки в которых происходит смена аналитических выражений. В данном случае только точки и(в остальных точках данная функция непрерывна).

Выясним будет ли точкой разрыва данной функции. Для этого найдем левосторонний и правосторонний пределы функции в данной точке:

.

Так как , то– точка разрыва, причем первого рода,поскольку оба односторонних предела конечные. Этот разрыв не устраним, т.к.

.

Точка есть точка разрыва данной функции второго рода, т.к.

.

В данном случае можно не вычислять.

Ответ: – точка разрыва первого рода,

–точка разрыва второго рода.

Задача 10

1) Найти производную функции

2) Найти производную функции

3) Найти производную функции: .

4) Найти производную функции: .

5) Найти производную функции: .

Задача 11. Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить ее график.

Решение

1. Область определения функции: пересечение оси0х в точке (1;0), а оси 0у - (0;-1);

2. точка разрыва;

3. Из 2) следует, что вертикальная асимптота;

Находим наклонную асимптоту:

–наклонная асимптота при

4. =

при(возрастает)

(убывает)

(возрастает)

(возрастает)

5. Из предыдущего 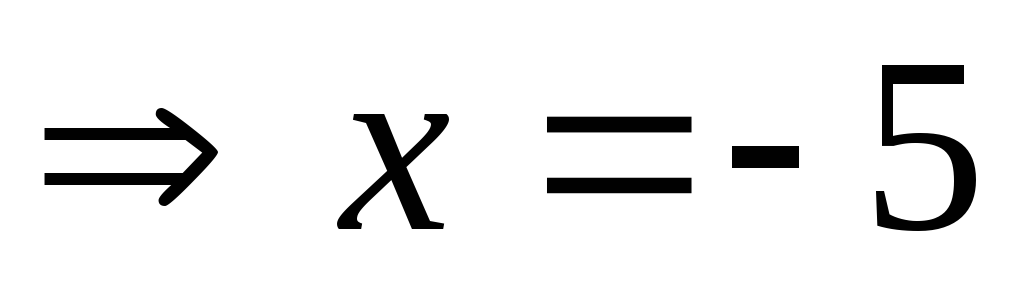точка максимума,

- max;

6. при ;

При

абсцисса точки перегиба, .

Результаты исследования внесем в следующую таблицу

х		-5	(-5;-1)	(-1;1)	1	(1;+4)
	+	0	-	+	0	+
	-	-	-	-	0	+
y		-27/2- max			0

Задача 12. Дана функция и две точки и . Требуется:

1) вычислить значение в точке ;

2) вычислить приближенное значение функции в точке , исходя из значения функции в точке и, заменив приращение функции при переходе от точки к точке дифференциалом;

3) оценить в процентах относительную погрешность, получающуюся при замене приращения функции ее дифференциалом;

4) составить уравнение касательной плоскости к поверхности

в точке .

Решение

1)

2) Т.к. приращение функции двух переменных

приближенно равно дифференциалу этой функции при и : ,

то .

Т.е. .

Имеем ; ; ;

; ; ; ; . Итак, приближенные значения функции в точке

.

3) Найдем относительную погрешность при замене на :

4) Т.к. уравнение касательной плоскости к поверхности в точке имеет вид ;

то имеем или

Задача 13. Найти наименьшее и наибольшее значение функции в замкнутой области , заданной системой неравенств , . Сделать чертеж.

y

2

D

C

B

A

x

1

0

Решение. Найдем стационарные точки функции внутри области , решая систему . Имеем, , , тогда решение системы есть точка . Но она не входит в область .

Исследуем теперь поведение функции на границе области . Найдем сначала стационарные точки функции внутри отрезков границы области.

а) Уравнение стороны прямоугольника: .

На стороне функция .

Найдем стационарные точки внутри отрезка

при

б) Уравнение стороны : .

На стороне прямоугольника функция .

, т.е. стационарных точек нет.

в) Уравнение стороны : .

На стороне прямоугольника функция .

при , т.е. внутри отрезка стационарных точек нет.

г) Уравнение стороны : .

На стороне функция , , т.е. стационарных точек нет.

Итак, функция не имеет стационарных точек ни внутри области , ни внутри отрезков границы области .

Найдем значения функции в вершинах прямоугольника и выберем среди них наименьшее и наибольшее.

.

Итак, ,

Задача 14. Даны функция , точка и вектор . Найти:

1) в точке ;

2) производную в точке по направлению вектора .

Решение.

1. Вектор .

Находим

Итак,

2. Производная функции в точке по направлению вектора находится по формуле

, где

– направляющие косинусы вектора .

Находим ,

.

Тогда .

Задача 15. Экспериментально получены пять значений функции при пяти значениях аргумента, которые записаны в таблице:

Методом наименьших квадратов найти функцию вида , выражающую (аппроксимирующую) функцию . Сделать чертеж, на котором в декартовой прямоугольной системе координат построить экспериментальные точки и график аппроксимирующей функции .

Решение. Найдем необходимые для расчетов суммы

y

5

1

1

x

5

Промежуточные вычисления оформим в виде вспомогательной таблицы.

	1 2 3 4 5	2,1 3,3 2,9 4,4 5,1	2,1 6,6 8,7 17,6 25,5	1 4 9 16 25
	15	17,8	60,5	55

Система нормальных уравнений

имеет вид .

Ее решение дает искомую зависимость: .

Задача 16. Найти полный дифференциал функции .

Решение. Найдем частные производные функции и воспользуемся формулой

.

.

Задача 17

1) Найти

Решение. Воспользуемся заменой переменной, получим

.

2) Найти.

Решение. Применим метод интегрирования по частям

.

3) Найти

Решение. Применим метод интегрирования по частям дважды

.

4) Найти

Решение. Разложим знаменатель подынтегральной рациональной функции на множители: Правильная дробь разлагается в сумму простейших дробей:Воспользовавшись методом неопределенных коэффициентов, найдем коэффициентыA, В, C. Приведем правую часть равенства к общему знаменателю и приравняем числители: Подставляем корни знаменателя:

Таким образом, искомое разложение на простейшие дроби имеет вид:

В результате получаем:

.

5) Найти

Решение. Разложим знаменатель на множители

.

Подынтегральная функция разложится на сумму простейших дробей:

Приведем правую часть равенства к общему знаменателю и приравняем числители: Подставляем корни знаменателя:

Для нахождения B, приравниваем коэффициенты при , получаем 1=A+B, откуда . Таким образом, искомое разложение на простейшие дроби имеет вид

В результате получаем:

.

6) Найти

Решение. Рациональная дробь – правильная и ее разложение на простейшие дроби имеет вид:Сравнивая числители дробей в обеих частях равенства, получимИмеется только один действительный корень, этого достаточно для нахождения только одного коэффициентаА:

Для нахождения остальных коэффициентов раскроем скобки в правой части равенства и запишем ее в виде многочлена четвертой степени:

Сравнивая коэффициенты при одинаковых степенях x левой и правой частях, получим систему уравнений для нахождения неопределенных коэффициентов

Отсюда находим Искомое разложение имеет вид

Следовательно

Второй и третий интеграл справа находим одинаковой заменой и окончательно получаем

7) Найти

Решение. Подынтегральная функция рационально зависит от и; применим подстановку, тогда

,,

и

Возвратившись к старой переменной, получим

8) Найти

Решение. Выполним замену переменной Числитель подынтегрального выражения можно представить следующим образом:

Поэтому имеем

Возвращаясь к переменной , получим

З

y

адача 18.Вычислить площадь фигуры, ограниченной параболой и прямой . Сделать чертеж.

2

1

5

0

х

3

5

Решение. Воспользуемся формулой , где – функция, график которой ограничивает фигуру сверху, а – снизу (на отрезке ).

.

Задача 19. Вычислить длину дуги цепной линии от до .

Решение. Длину дуги вычислим по формуле .

Найдем : или . Тогда

Задача 20. Найти общее решение дифференциального уравнения xy’ + 2y = x² и частное решение, удовлетворяющее начальному условию при.

Решение. Полагаем y = u (x) v(x), находим y’ = u’v + uv’. Подставим вместо y и y’ соответствующие выражения в исходное уравнение:

x (u’v + uv’) + 2uv = x², илиxu’v + u ( xv’ + 2v ) = x². (*)

Подберем v = v ( x ) так, чтобыxv’ + 2v = 0, или , откудаинтегрируя, имеем или

Уравнение (*) примет вид:

u’v = x, илиu’= x, отсюдаu’ = x³, du = x³ dx, u =

у = u (x) v (x) = или - общее решение.

Найдем частное решение данного уравнения, удовлетворяющее начальному условию при: , откуда . Таким образом, - частное решение.

Задача 21. Найти общее решение дифференциального уравнения .

Решение. Поскольку это уравнение однородное то применим подстановку , тогда . После подстановки в уравнение получим . Разделим переменные: . Интегрируя левую часть равенства по u, а правую – по x, получим:

Вернемся к прежней переменной:

. Общий интеграл: .

Задача 22. Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальным условиям при .

Решение. Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами.

Найдем – общее решение соответствующего однородного уравнения

. Составим характеристическое уравнение: . Его корни действительные различные, поэтому .

Т.к. правая часть неоднородного уравнения и не корень характеристического уравнения, то частное решение неоднородного уравнения следует искать в виде: .

Находим . Подставляя в неоднородное уравнение, получим .

Итак, .

Общее решение линейного неоднородного уравнения , поэтому общее решение .

Найдем частное решение, удовлетворяющее начальным условиям .

Т.к. , то имеем систему уравнений для нахождения постоянных и :

.

Итак, искомое частное решение: .

Задача 23. Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям .

Решение. Имеем линейное неоднородное уравнение с постоянными коэффициентами. Найдем – общее решение соответствующего однородного уравнения . Для этого составим характеристическое уравнение . Его корни комплексные, поэтому .

Т.к. правая часть неоднородного уравнения и - не корень характеристического уравнения, то частное решение неоднородного уравнения следует искать в виде . Находим

.

Подставляем в неоднородное уравнение, получим

.

Итак, .

Общее решение линейного неоднородного уравнения , поэтому общее решение .

Найдем частное решение, удовлетворяющее условиям .

Т.к. , то имеем систему уравнений для нахождения постоянных

.

Итак, искомое частное решение: .

Задача 24. Исследовать сходимость числового ряда

Решение. Воспользуемся признаком Даламбера:

, поэтому ряд сходится.

Задача 25. Найти область сходимости степенного ряда.

Решение. Имеем . Находим радиус сходимости

, (-10, 10) – интервал сходимости.

Исследуем на сходимость степенной ряд на концах интервала сходимости:

а) при получаем числовой ряд , который сходится по признаку Лейбница.

б) при x=10 получаем расходящийся гармонический ряд .

Итак, [-10, 10) - область сходимости.

Задача 26. Написать три первых члена степенного ряда по заданному общему члену найти интервал сходимости ряда и исследовать его сходимость на концах этого интервала.

Решение.

Интервал сходимости этого степенного ряда с центром в нуле имеет вид <-R;R>. Радиус сходимости R найдем по формуле , где – коэффициенты степенного ряда.

Имеем , поэтому = . Итак, <-5;5> – интервал сходимости.

При имеем ряд , который расходится ( сходится при и расходится при ).

При получаем ряд , который сходится по признаку Лейбница (знакочередующийся ряд, модули членов которого убывают и стремятся к нулю). Итак, [-5;5) – область сходимости данного ряда.

Задача 27. Вычислить определенный интеграл с точностью до 0,001, разложив подинтегральную функцию в степенной ряд и затем проинтегрировав его почленно.

Решение. Заменив на в разложении

,

получим .

Умножая полученный ряд на

и почленно интегрируя по отрезку , принадлежащему интервалу сходимости ряда , получим

Взяв первые шесть членов разложения, на основании следствия из теоремы Лейбница для сходящегося знакочередующегося ряда мы допустим погрешность , не превышающую первого отброшенного члена (по абсолютной величине), т.е.

.

Итак,

.

Задача 28. Выразить определенный интеграл в виде сходящегося ряда, используя ряд Маклорена для подинтегральной функции. Найти приближенное значение этого интеграла с точностью до 0,001.

Решение. Заменив на в разложении получим .

Умножая полученный ряд на

и почленно интегрируя по отрезку , принадлежащему интервалу сходимости ряда , получим

Взяв первые четыре члена разложения, на основании следствия из теоремы Лейбница для сходящегося знакочередующегося ряда мы допустим погрешность , не превышающую первого отброшенного члена (по абсолютной величине), т.е.

.

Итак, .

Задача 29. Два стрелка стреляют по мишени. Вероятность попадания первым стрелком равна 0.8, вторым – 0.9. Найти вероятность того, что при залпе по мишени попадет только один стрелок.

Решение. Пусть событие А₁ – первый стрелок попал по мишени, А₂ – второй стрелок попал по мишени, В – при залпе по мишени попал только один стрелок. Событие В словами можно описать следующим образом: при залпе по мишени (первый стрелок попал, а второй промахнулся) или (второй стрелок попал, а первый промахнулся). Событие означает, что при залпе по мишени промахнулся первый стрелок,– промахнулся второй. Произведение событийозначает, что при залпе по мишени первый стрелок промахнулся, а второй при этом попал по мишени,– первый попал и второй промахнулся. Тогда. Событияинесовместные, следовательно(события А₁ и А₂ независимые, следовательно, события итак же независимые) =(по теореме о вероятности произведения независимых событий) == () =

Задача 30. Случайная величина X задана функцией распределения

Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины.

Решение. Найдем плотность распределения вероятностей случайной величины X:

.

Математическое ожидание случайной величины X:

.

Дисперсия случайной величины X:

.

Задача 31. Найти доверительный интервал для оценки математического ожидания нормального распределения с надежностью , зная выборочную среднюю , объем выборки и среднее квадратическое отклонение .

Решение. Справедливо равенство: , т.е. с надежностью можно утверждать, что доверительный интервал покрывает неизвестный параметр ; точность оценки .. Найдем . Из соотношения получим . По таблице значений функции находим .

Найдем точность оценки . Доверительный интервал таков: . При доверительный интервал имеет следующие доверительные границы: ;

.

Таким образом, значения неизвестного математического ожидания нормального распределения, согласующиеся с данными выборки, удовлетворяют неравенству .

Задача 32. В каждой из трех урн содержится 6 черных и 4 белых шара. Из первой урны наудачу извлечен один шар и переложен во вторую урну, после чего из второй урны наудачу извлечен один шар и переложен в третью урну. Найти вероятность того, что шар, наудачу извлеченный из третьей урны, окажется белым.

Решение. Обозначим через А событие – из третьей урны извлечен белый шар.

6 - Ч

4 - Б

6 - Ч

4 - Б

6 - Ч

4 - Б

Б

Рассмотрим все возможные случаи извлечения шаров из урн: БББ, ББЧ, БЧБ, БЧЧ, ЧБЧ, ЧББ, ЧЧБ, ЧЧЧ. Из восьми возможных случаев, только четыре удовлетворяют условию, что из третьей урны извлечен белый шар. Введем обозначения

- из 1-ой урны извлечен белый шар;

- из 1-ой урны извлечен черный шар;

- из 2-ой урны извлечен белый шар;

- из 2-ой урны извлечен черный шар.

Поскольку в первой урне содержится всего 10 шаров, причем 4 из них белых, то вероятность события . Соответственно вероятность того, что из первой урны будет извлечен черный шар равна:Условная вероятность того, что из 2-ой урны будет извлечен белый шар, при условии, что из 1-ой урны был извлечен белый шар равнаУсловная вероятность того, что из 2-ой урны будет извлечен белый шар, при условии, что из 1-ой урны был извлечен черный шар равна:Вычислим условную вероятность событияпри условияхи:и

Вероятность того, что из 3-ой урны будет извлечен белый шар, при условии, что и из 1-ой и из 2-ой урн были извлечены белые шары равна: Вероятность события, при условиях,равна:Условная вероятность, с учетом того, что из 1-ой урны извлечен черный шар, а из 2-ой урны извлечен белый шар равна:

Вероятность события , при условиях,равна:Искомую вероятность того, что из третьей урны будет извлечен белый шар, находим по формуле полной вероятности:

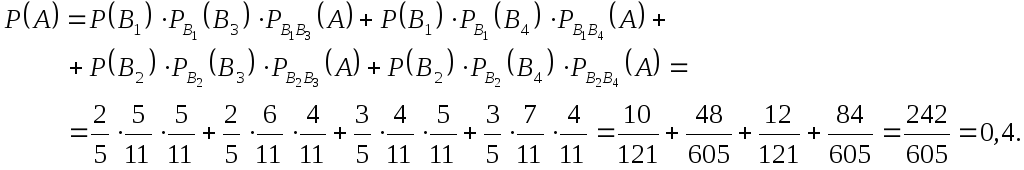
Задача 33. Имеется три партии деталей по 20 деталей в каждой. Число стандартных деталей в первой, второй и третьей партиях соответственно равно 20, 16, 6. Из наудачу взятой партии наудачу извлечена деталь, оказавшаяся стандартной. Затем из той же партии вторично наудачу извлекли деталь, также оказавшуюся стандартной. И, наконец, из той же партии в третий раз наудачу извлекли деталь, которая также оказалась стандартной. Найти вероятность того, что детали были извлечены из второй партии.

Решение. Обозначим через А событие – в каждом из трех испытаний была извлечена стандартная деталь. Можно сделать три предположения (гипотезы): - детали извлекались из первой партии,- детали извлекались из второй партии,- детали извлекались из третьей партии.

Детали извлекались из наудачу взятой партии, поэтому вероятности гипотез одинаковы:

Найдем условную вероятность , т.е. вероятность того, что из первой партии будут последовательно извлечены три стандартные детали. Это событие достоверно, так как в первой партии все детали стандартны, поэтому

Найдем условную вероятность , т.е. вероятность того, что из второй партии будут последовательно извлечены (без возращения) три стандартные детали:

Найдем условную вероятность , т.е. вероятность того, что из третьей партии будут последовательно извлечены (без возращения) три стандартные детали:

Искомая вероятность того, что три извлеченные стандартные детали взяты из второй партии, по формуле Бейеса равна

Задача 34. Случайная величина X задана функцией распределения F(x):

Требуется:

а) найти плотность распределения вероятностей;

б) построить графики интегральной и дифференциальной функций;

в) найти математическое ожидание и дисперсию случайной величины X;

г) определить вероятность того, что X примет значение, заключенное в интервале

Решение. а) Плотность распределения вероятностей равна первой производной от функции распределения:

б) Построим графики интегральной и дифференциальной функций:

в) Найдем математическое ожидание и дисперсию случайной величины X. Поскольку случайная величина X задана плотностью распределения в интервале, а вне этого интервалато воспользуемся следующей формулой

Подставив получим

Дисперсию случайной величины найдем по следующей формуле:

Подставляем известные нам данные и получаем

г) Определим вероятность того, что X примет значение, заключенное в интервале

Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу , определяется равенством

Таким образом

Задача 35. Дано статистическое распределение выборки

	12	14,5	17	19,5	22	24,5	27
	4	17	33	60	55	24	7

Требуется:

1. Найти методом произведений выборочные: среднюю, дисперсию и среднее квадратическое отклонение, асимметрию и эксцесс.

2. Построить нормальную кривую.

3. Найти доверительный интервал для оценки неизвестного математического ожидания M(X), полагая, что X имеет нормальное распределение, среднее квадратическое отклонение и доверительная вероятность.

Решение. 1. Составим расчетную табл. 1. Для этого:

• запишем варианты в первый столбец;

• запишем частоты во второй столбец; сумму частот (200) по­местим в нижнюю клетку столбца;

• в качестве ложного нуля С выберем варианту (19,5), которая имеет наибольшую частоту (в качестве С можно взять любую варианту, расположенную примерно в середине столбца); в клетке третьего столбца, которая принадлежит строке, содержащей ложный нуль, пишем 0; над нулем последовательно записываем -1, -2, -3, а под нулем 1, 2, 3;

• произведения частот на условные варианты запишем в четвертый столбец; сложив эти числа, их сумму (45) помещаем в нижнюю клетку четвертого столбца;

• произведения частот на квадраты условных вариант, т. е. 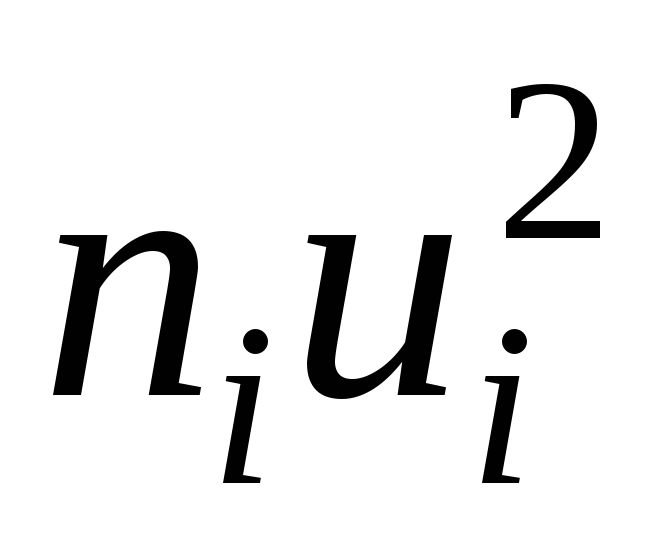запишем в пятый столбец (удобнее перемножить числа каждой строки третьего и четвертого столбцов: ∙=); сумму чисел столбца (351) помещаем в нижнюю клетку пятого столбца;

• Для заполнения столбца 6 удобно перемножить числа каждой строки третьего и пятого столбцов.

• Для заполнения столбца 7 удобно перемножить числа каждой строки третьего и шестого столбцов.

• Произведения 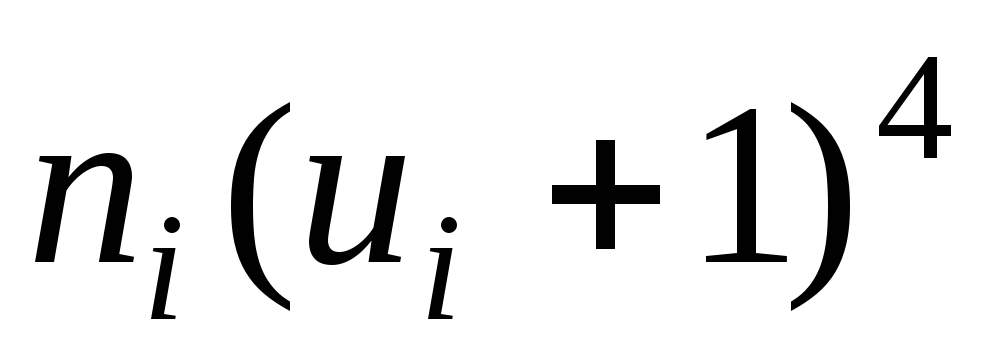запишем в восьмой контрольный столбец; сумму чисел столбца (4757) помещаем в нижнюю клетку восьмого столбца. Столбец 8 служит для контроля вычислений с помощью тождества

∑=∑+4∑+6∑+4∑+.

В итоге получим расчетную табл. 1.

Таблица 1

1	2	3	4	5	6	7	8
12	4	-3	-12	36	-108	324	64
14,5	17	-2	-34	68	-136	272	17
17	33	-1	-33	33	-33	33	0
19,5	60	0	0	0	0	0	60
22	55	1	55	55	55	55	880
24,5	24	2	48	96	192	384	1944
27	7	3	21	63	189	567	1792
∑	200		45	351	159	1635	4757

Контроль: ∑=4757,

∑+4∑+6∑+4∑+=1635+4∙159+6∙351+4∙45+200=4757.

Совпадение контрольных сумм свидетельствует о правильности вычислений.

Вычислим условные моменты первого, второго, третьего и четвертого порядков:

===0,225;===1,755;

===0,795;===8,175.

Найдем шаг (разность между любыми двумя соседними вариантами):

h = 14,5-12 = 2,5.

Вычислим искомые выборочные среднюю и дисперсию, учитывая что ложный нуль (варианта, которая имеет наибольшую частоту) С = 19,5:

.

.

Найдем центральные эмпирические моменты третьего и четвертого порядков:

,

Найдем асимметрию и эксцесс:

;

.

2. Для построения нормальной кривой найдем ординаты (выравнивающие частоты) теоретической кривой по формуле , где- сумма наблюдаемых частот (объем выборки),- разность между двумя соседними вариантами,и. Затем строим точкив прямоугольной системе координат и соединяем их плавной кривой. Все вычисления запишем в табл. 2.

Таблица 2

12	4	-8,0625	-2,470	0,019	3
14,5	17	-5,5625	-1,704	0,094	15
17	33	-3,0625	-0,938	0,257	40
19,5	60	-0,5625	-0,172	0,3932	60
22	55	1,9375	0,594	0,3352	52
24,5	24	4,4375	1,360	0,1582	24
27	7	6,9375	2,126	0,042	6

3. Требуется найти доверительный интервал для оценки неизвестного математического ожидания M(X):

.

Все величины, кроме , известны. Найдемиз соотношения

. По таблице значений функции находим. Подставляя=20,0625,=3,264,=200, вычислим=19,61 ,=20,51. Окончательно получим искомый доверительный интервал 19,61<<20,51.

Задача 36. Найти: 1) выборочное уравнение прямой регрессии на ; 2) выборочное уравнение прямой регрессии на .

Построить диаграмму рассеивания и графики уравнений регрессии по данной корреляционной таблице:

Решение. Выберем “ложные” нули: . Запишем таблицу в условных вариантах.

Найдем вспомогательные величины:

;

;

;

;

;

;

;

;

;

;

.

Для вычисления суммы составим таблицу

	(-3 1 -4)
	(-6 2 -6)	(-4 2 -6)	(-1 1 -3)
		(-8 4 -8)	(-3 3 -6)	(0 2 -4)
		(-2 1 -1)	(-6 6 -6)	(0 11 -11)	(4 4 -4)
			(-5 5 0)	(0 8 0)	(15 15 0)
				(0 4 4)	(7 7 7)	(12 6 6)
					(5 5 10)	(8 4 8)
					(1 1 3)	(4 2 6)	(9 3 9)
						(2 1 4)	(6 2 8)

Тогда

Найдем уравнения регрессий: ;

или ;

; или

. Для построения диаграммы рассеивания найдем групповые средние: ; ;

; ;

;

; ; ;

; ;

; ;

; ;

; .

Изобразим диаграмму рассеивания (точки) и графики уравнений регрессии.

Задача 37. Найти максимальное значение линейной функции при ограничениях

Решение. Построим многоугольник решений. Для этого в системе координат на плоскости изобразим граничные прямые

Взяв какую-нибудь, например, начало координат, установим, какую полуплоскость определяет соответствующее неравенство (эти полуплоскости на рисунке показаны стрелками). Многоугольником решений данной задачи является ограниченный пятиугольник ОАВСD.

Для построения прямой строим радиус-вектор = (50;40)=10 (5;4) и через точку О проводим прямую, перпендикулярную ему. Построенную прямую Z=0 перемещаем параллельно самой себе в направлении вектора . Из рис. 1.3 следует, что опорной по отношению к многоугольнику решении эта прямая становится в точке С, где функция Z принимает максимальное значение. Точка С лежит на пересечении прямых . Для определения её координат решим систему уравнении

Оптимальный план задачи: Подставляя значенияв линейную функцию, получаем

8

А

4

0 D 5

Таким образом, для того чтобы получить максимальную прибыль в размере 260,3 руб., необходимо запланировать производство 3,9 ед. продукции и 1,7 ед. продукции

Задача 38. Для изготовления различных изделий А, В и С пред­приятие использует три различных вида сырья. При этом на изготовление единицы изделия вида А расходуется 18 кг материала первого вида, 6 кг материала второго вида и 5 кг материала третьего вида. На изготовление единицы изделия вида расходуется 15 кг материала первого вида, 4 кг материала второго вида, 3 кг материала третьего вида. На изготовление единицы изделия видаC расходуется 12 кг материала первого вида, 8 кг материала второго вида, 3 кг материала третьего вида. На складе фабрики имеется всего материала первого вида 360 кг, материала второго вида 192 кг, материала третьего вида 180 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль 9 руб., продукции вида В прибыль составляет 10 руб., продукции вида С прибыль составляет 16 руб.

Определить максимальную прибыль от реализации всей продукции видов А, В и С. Решить задачу симплекс-методом.

Решение. Запишем данные задачи в таблицу.

Вид сырья	Нормы затрат сырья (кг) на одно изделие вида			Общее количество сырья (кг)
	А	В	С
I	18	15	12	360
II	6	4	8	192
III	5	3	3	180
Прибыль от реализации единицы продукции	9	10	16

Составим математическую модель задачи. Введем новые переменные:

количество выпускаемых изделий вида А;

количество выпускаемых изделий вида В;

количество выпускаемых изделий вида С.

Так как на 1 изделие вида А предприятие расходует 18 кг сырья первого вида, то на производство общего количества продукции вида А предприятию потребуется кг того же материала. Соответственно для производства всей продукции видаВ и С предприятию потребуется кг исырья первого вида соответственно. Поскольку расходы на производство не должны превышать общего количества сырья имеющегося на складе, то при изготовленииединиц изделий видаА,единиц изделий видаВ и единиц изделий видаС должно быть израсходовано не более 360 кг сырья первого вида. Таким образом, все выше сказанное можем записать в виде неравенства:

Аналогично, при затратах, на производство продукции вида А, В и С, сырья второго и третьего сорта предприятие должно учитывать количество данного сырья, имеющегося на складе. Т.е. необходимо выполнение следующих неравенств:

При этом так как количество изготовляемых изделий не может быть отрицательным, то

Далее, если будет изготовлено единиц изделий видаА, единиц изделий видаВ и единиц изделий видаС, то прибыль от их реализации составит

Таким образом, приходим к следующей математической задаче:

(1)

(2)

среди всех неотрицательных решений системы нера­венств (2) требуется найти такое, при котором функция (1) принимает максимальное значение.

Запишем эту задачу в форме основной задачи линейного программирования. Для этого перейдем от ограничений-нера­венств к ограничениям-равенствам. Введем три дополнительные переменные, в результате чего ограничения запишутся в виде системы уравнений

Эти дополнительные переменные означают не используемое при данном плане производства количество сырья того или иного сорта (например, - неиспользуемое количество материалаI вида).

Преобразованную систему уравнений запишем в векторной форме:

где ;;;;;.

Поскольку среди векторов имеются триединичных вектора, для данной задачи можно непосредственно записать опорный план. Таковым является план Х=(0; 0; 0; 360; 192; 180), определяемый системой трехмерных единичных векторов , которые образуют базис трехмерного век­торного пространства.

Составляем симплексную таблицу для I итерации (табл. 1.1). В столбец записываем коэффициенты при базисных векторах в целевой функции. Коэффициенты 4-й строки вычисляются по формулам: и проверяем исходныйопорный план на оптимальность:

Таблица 1.1

	Базис			9	10	16	0	0	0
1		0	360	18	15	12	1	0	0
2		0	192	6	4	8	0	1	0
3		0	180	5	3	3	0	0	1
4			0	-9	-10	-16	0	0	0

Как видно из табл. 1.1, значения всех основных переменных равны нулю, а дополнительные переменные принимают свои значения в соответствии с ограничениями задачи. Эти значения переменных отвечают такому «плану», при котором ничего не производится, сырье не используется и значение це­левой функции равно нулю (т. е. стоимость произведенной про­дукции отсутствует). Этот план, конечно, не является оптималь­ным.

Это видно и из 4-й строки табл. 1.1, так как в ней имеется три отрицательных числа: . Отрицательные числа не только свидетельствуют о воз­можности увеличения общей стоимости производимой продук­ции, но и показывают, на сколько увеличится эта сумма при введении в план единицы того или другого вида продукции. Так, число -9 означает, что при включении в план произ­водства одного изделия А обеспечивается увеличение выпуска продукции на 9 руб. Если включить в план производства по од­ному изделию В и С, то общая стоимость изготовляемой про­дукции возрастет соответственно на 10 и 16 руб. Поэтому с экономической точки зрения наиболее целесообразным является включение в план производства изделий С. Это же необходимо сделать и на основании формального признака симплексного метода, поскольку максимальное по абсолютной величине отри­цательное число стоит в 4-й строке столбца вектора Р₃. Сле­довательно, в базис введем вектор . Определяем вектор, под­лежащий исключению из базиса. Для этого находим длят.е.

Найдя число 192/8 = 24, мы тем самым с экономической точки зрения определили, какое количество изделий С пред­приятие может изготовлять с учетом норм расхода и имеющих­ся объемов сырья каждого вида. Так как сырья данного вида соответственно имеется 360, 192 и 180 кг, а на одно изделие С требуется затратить сырья каждого вида соответственно 12, 8 и 3 кг, то максимальное число изделий С, которое может быть изготовлено предприятием, равно , т.е. ограничивающим фактором для производства изделий С является имеющийся объем сырья II вида. С учетом его наличия предприятие может изготовить 24 изделия С. При этом сырье II вида будет полностью использовано.

Следовательно, вектор подлежит исключению из базиса. Столбец вектора и 2-я строка являются направляющими. Элемент, стоящий на пересечении столбца и 2-й строки, называется разрешающим элементом.Составляем таблицу для II итерации (табл. 1.2).

Таблица 1.2

	Базис			9	10	16	0	0	0
1		0	72	9	9	0	1		0
2		16	24			1	0		0
3		0	108			0	0		1
4			384	3	-2	0	0	2	0

Сначала заполняем строку вектора, вновь введенного в ба­зис, т.е. строку, номер которой совпадает с номером направ­ляющей строки. Здесь направляющей является 2-я строка. Эле­менты этой строки табл. 1.2 получаются из соответствующих элементов табл. 1.1 делением их на разрешающий элемент (т.е. на 8). При этом в столбце записываем коэффициент , стоящий в столбце вводимого в базис вектора . Затем запол­няем элементы столбцов для векторов, входящих в новый базис. В этих столбцах на пересечении строк и столбцов одноимен­ных векторов проставляем единицы, а все остальные элементы полагаем равными нулю.

Для определения остальных элементов табл. 1.2 применяем правило прямоугольника:

a c

d

b , где - пересчитанный коэффициент новой таблицы,

d – разрешающий элемент,

b, c – элементы, стоящие на диагонали прямоугольника.

Вычислим элементы табл. 1.2, стоящие в столбце вектора Первый из них находится в 1-й строке этого столбца. Получаем:

; записываем его в 1-й строке столбца вектора табл. 1.2.

Второй элемент столбца вектора табл. 1.2 был уже вычис­лен ранее. Вычисляем третий элемент столбца вектора :.Число 108 записываем в 3-й строке столбца вектора табл. 1.2.

Значение в 4-й строке столбца этого же вектора можно найти двумя способами:

1. по формуле ,т.е.

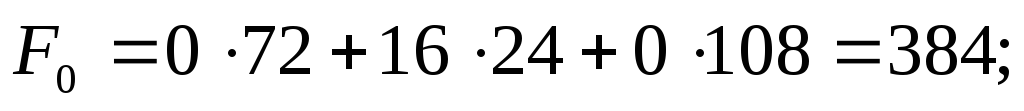
2. по правилу прямоугольника; в данном случае прямоугольник образован числами 0, 192, 8, -16. Этот способ приводит к тому же результату: .

Аналогично пересчитываем оставшиеся элементы табл. 1 и записываем их в новую табл. 2.

По окончании расчета всех элементов табл. 1.2 в ней полу­чены новый опорный план и коэффициенты разложения векторов через базисные векторы и значения . Как видно из этой таблицы, новым опорным планом задачи является план . При данном планепроизводства изготовляется 24 изделия С и остается неисполь­зованным 72 кг сырья I вида и 108 кг сырья III вида. Стоимость всей производимой при этом плане продукции равна 384 руб. Указанные числа записаны в столбце вектора табл. 1.2. Как видно, данные этого столбца по-прежнему представляют собой параметры рассматриваемой задачи, хотя они претерпели зна­чительные изменения. Изменились данные и других столбцов, а их экономическое содержание стало более сложным. Так, на­пример, возьмем данные столбца вектора Число во 2-й строке этого столбца показывает, на сколько следует уменьшить изготовление изделий С, если запланировать выпуск одного изделия В. Числа 9 и в 1-й и 3-й строках вектора пока­зывают соответственно, сколько потребуется сырья I и II вида при включении в план производства одного изделия B, а число -2 в 4-й строке показывает, что если будет запланирован вы­пуск одного изделия В, то это обеспечит увеличение выпуска продукции в стоимостном выражении на 2 руб. Иными слова­ми, если включить в план производства продукции одно изде­лие В, то это потребует уменьшения выпуска изделия С на ед. и потребует дополнительных затрат 9 кг сырья I вида и кг сырья III вида, а общая стоимость изготовляемой продукции в соответствии с новым оптимальным планом возрастет на 2 руб. Таким образом, числа 9 и выступают как бы новыми «норма­ми» затрат сырья I и III вида на изготовление одного изделия В (как видно из табл. 1.1, ранее они были равны 15 и 3), что объясняется уменьшением выпуска изделий С.

Такой же экономический смысл имеют и данные столбца век­тора табл. 1.2. Несколько иное экономическое содержание имеют числа, записанные в столбце вектора . Число во 2-й строке этого столбца, показывает, что увеличение объемов сырья II вида на 1 кг позволило бы увеличить выпуск изделий С на ед. Одновременно потребовалось бы дополнительно кг сырья I вида и кг сырья III вида. Увеличение выпуска изделий С на ед. приведет к росту выпуска продукции на 2 руб.

Из изложенного выше экономического содержания данных табл. 1.2 следует, что найденный на II итерации план задачи не является оптимальным. Это видно и из 4-й строки табл. 1.2, поскольку в столбце вектора этой строки стоит отрицатель­ное число -2. Значит, в базис следует ввести вектор , т. е. в новом плане следует предусмотреть выпуск изделий В. При определении возможного числа изготовления изделий В следует учитывать имеющееся количество сырья каждого вида, а именно: возможный выпуск изделий В определяется длят.е. находим .

Следовательно, исключению из базиса подлежит вектор , иными словами, выпуск изделий В ограничен имеющимся в распоряжении предприятия сырьем I вида. С учетом имеющих­ся объемов этого сырья предприятию следует изготовить 8 изде­лий В. Число 9 является разрешающим элементом, а столбец вектора и 1-я строка табл. 1.2 являются направляющими. Составляем таблицу для III итерации (табл. 1.3).

Таблица 1.3

	Базис			9	10	16	0	0	0
1		10	8	1	1	0			0
2		16	20		0	1			0
3		0	96		0	0			1
4			400	5	0	0			0

В табл. 1.3 сначала заполняем элементы 1-й строки, которая представляет собой строку вновь вводимого в базис вектора . Элементы этой строки получаем из элементов 1-й строки табл. 1.2 делением последних на разрешающий элемент (т.е. на 9). При этом в столбце данной строки записываем

Затем заполняем элементы столбцов векторов базиса и по правилу прямоугольника вычисляем элементы остальных столб­цов. В результате в табл. 3 получаем новый опорный план и коэффициенты разложения векторов через базисные векторы и соответствующие значения

Проверяем, является ли данный опорный план оптимальным или нет. Для этого рассмотрим 4-ю строку табл. 1.3. В этой строке среди чисел нет отрицательных. Это означает, что найден­ный опорный план является оптимальным и

Следовательно, план выпуска продукции, включающий из­готовление 8 изделий В и 20 изделий С, является оптимальным. При данном плане выпуска изделий полностью используется сырье I и II видов и остается неиспользованным 96 кг сырья III вида, а стоимость производимой продукции равна 400 руб.

Оптимальным планом производства продукции не предусмат­ривается изготовление изделий А. Введение в план выпуска про­дукции изделий вида А привело бы к уменьшению указанной общей стоимости. Это видно из 4-й строки столбца вектора , где число 5 показывает, что при данном плане включение в него выпуска единицы изделия А приводит лишь к уменьшению об­щей величины стоимости на 5 руб.

Ответ: максимальная прибыль от реализации всей продукции составляет 400 руб.

Задача 39

1) На три базы поступил однородный груз в ко­личествах, соответственно равных 140, 180 и 160 ед. Этот груз требуется перевезти в пять пунктов назначениясоответственно в количествах 60, 70, 120, 130 и 100 ед. Тарифы перевозок единицы груза с каждого из пунктов отправления в со­ответствующие пункты назначения указаны в следующей таблице:

Таблица 2.1

Пункты отправления	Пункты назначения					Запасы
	2	3	4	2	4	140
	8	4	1	4	1	180
	9	7	3	7	2	160
Потребности	60	70	120	130	100	480

Найти план перевозок данной транспортной задачи методом северо-западного угла.

Решение. При нахождении опорного плана транспортной задачи методом северо-западного угла на каждом шаге рассматривают первый из оставшихся пунктов отправления и первый из оставшихся пунктов назначе­ния. Заполнение клеток таблицы условий начинается с левой верхней клетки для неизвестного («северо-западный угол») и заканчивается клеткой для неизвестного, т. е. идет как бы по диагонали таблицы.

Здесь число пунктов отправления , а число пунктов назначенияСледовательно, опорный план задачи определяется числами, стоящими взаполненных клетках.

Заполнение таблицы начнем с клетки для неизвестного , т. е. попытаемся удовлетворить потребности первого пункта назначе­ния за счет запасов первого пункта отправления. Так как запасы пункта больше, чем потребности пункта, то полагаем , записываем это значение в соответствующей клетке табл.1и временно исключаем из рассмотрения столбец, считая при этом запасы пунктаравными 80.

Таблица 2.2

Пункты отправления	Пункты назначения										Запасы
	2		3		4		2		4		140
		60		70		10
	8		4		1		4		1		180
						110		70
	9		7		3		7		2		160
								60		100
Потребности	60		70		120		130		100		480

Рассмотрим первые из оставшихся пунктов отправления и назначения. Запасы пунктабольше потребностей пункта. Положим , запишем это значение в соответствующей клетке табл. 2.2 и временно исключим из рассмотрения стол­бец . В пунктезапасы считаем равными 10 ед. Снова рассмо­трим первые из оставшихся пунктов отправленияи назначе­нияПотребности пунктабольше оставшихся запасов пункта. Положим и исключим из рассмотрения стро­ку .Значение запишем в соответствующую клетку табл. 2.2 и считаем потребности пункта равными 110 ед.

Теперь перейдем к заполнению клетки для неизвестного и т. д. Через шесть шагов остается один пункт отправления с запасом груза 100 ед. и один пункт назначенияс потреб­ностью 100 ед. Соответственно имеется одна свободная клетка, которую и заполняем, полагая (табл. 2.2). В резуль­тате получаем опорный план

Согласно данному плану перевозок, общая стоимость перево­зок всего груза составляет

2) Четыре предприятия для производства продукции используют три вида сырья. Потребности в сырье каждого из предприятий соответственно равны 120, 50, 190, 110 ед. Сырье сосредоточено в трех местах его получения, а запасы соответственно равны 160, 140, 170 ед. На каждое из предприятий сырье может завозиться из любого пункта его получения. Тарифы перевозок являются известными величинами и задаются матрицей

Найти опорный план транспортной задачи методом минимального элемента.

Решение. В методе се­веро-западного угла на каждом шаге потребности первого из оставшихся пунктов назначения удовлетворялись за счет запа­сов первого из оставшихся пунктов отправления. Очевидно, выбор пунктов назначения и отправления целесообразно произ­водить, ориентируясь на тарифы перевозок, а именно: на каждом шаге следует выбирать какую-нибудь клетку, отвечающую мини­мальному тарифу (если таких клеток несколько, то следует вы­брать любую из них), и рассмотреть пункты назначения и отправ­ления, соответствующие выбранной клетке. Сущность метода минимального элемента и состоит в выборе клетки с минималь­ным тарифом. Следует отметить, что этот метод, как правило, позволяет найти опорный план транспортной задачи, при котором общая стоимость перевозок груза меньше, чем общая стоимость перевозок при плане, найденном для данной задачи с помощью метода северо-западного угла. Поэтому наиболее целесообразно опорный план транспортной задачи находить методом минималь­ного элемента.

Исходные данные задачи запишем в виде табл. 3.1.

Таблица 3.1

Пункты отправления	Пункты назначения								Запасы
	7		8		1		2		160
						160
	4		5				8		140
		120						20
	9		2		3		6		170
				50		30		90
Потребности	120		50		190		110		470

Минимальный тариф, равный 1, находится в клетке для переменной . Положимзапишем это значение в соот­ветствующую клетку табл. 3.1 и исключим временно из рассмо­трения строку. Потребности пункта назначениясчитаем равными 30 ед.

В оставшейся части таблицы с двумя строками ии че­тырьмя столбцамиклетка с наименьшим значением тарифанаходится на пересечении строкии столбца, где. Положими внесем это значение в соответ­ствующую клетку табл. 3.1.

Временно исключим из рассмотрения столбец и будем счи­тать запасы пунктаравными 120 ед. После этого рассмотрим оставшуюся часть таблицы с двумя строкамии тремя столбцами. В ней минимальный тарифнаходится в клетке на пересечении строкии столбцаи равен 3. Заполним описанным выше способом эту клетку и аналогично запол­ним (в определенной последовательности) клетки, находящиеся на пересечении строкии столбца, строкии столбца, строкии столбца. В результате получим опорный план

При данном плане перевозок общая стоимость перевозок со­ставляет

3) Имеются три пункта поставки однородного груза и четыре пункта потребления этого груза. На пунктах находится груз соответственно в количестве 50, 30 и 10 т. В пункты требуется доставить соответственно 30, 30, 10, 20 т груза. Расстояние между пунктами потребления задано следующей матрицей:

Найти оптимальный план транспортной задачи.

Решение. Сначала, используя метод северо-западного угла, находим опорный план задачи. Этот план записан в табл. 4.1

Таблица 4.1

Пункты отправления	Пункты назначения								Запасы
	1		2		4		1		50
		30		20
	2		3		1		5		30
				10		10		10
	3		2		4		4		10
								10
Потребности	30		30		10		20		90

Найденный опорный план проверяем на оптимальность. В свя­зи с этим находим потенциалы пунктов отправления и назначения. Для определения потенциалов получаем систему

содержащую шесть уравнений с семью неизвестными. Полагая находимДля каждой свободной клетки вычисляем число :

Заключаем найденные числа в рамки и записываем их в каж­дую из свободных клеток табл. 4.2.

Так как среди чисел имеются положительные, то по­строенный план перевозок не является оптимальным и надо пе­рейти к новому опорному плану. Наибольшим среди положитель­ных чиселявляютсяпоэтому для данной свободной клетки строим цикл пересчета (табл. 4.2) и производим сдвиг по этому циклу.

Таблица 4.2

Пункты отправления	Пункты назначения								Запасы
	1		2	–	4		1	+	50
		30		20		-4		3
	2		3	+	1		5	–	30
		0		10		10		10
	3		2		4		4		10
		-2		0		-4		10
Потребности	30		30		10		20		90

Наименьшее из чисел в минусовых клетках рав­но 10. Клетка, в которой находится это число, становится свобод­ной в новой табл. 4.3. Другие числа в табл. 4.3 получаются так: к числу 10, стоящему в плюсовой клетке табл. 4.2, добавим 10 и вычтем 10 из числа 20, находящегося в минусовой клетке табл. 4.2. Клетка на пересечении строки и столбцастано­вится свободной.

После этих преобразований получаем новый опорный план (табл. 4.3).

Таблица 4.3

Пункты отправления	Пункты назначения								Запасы
	1		2	–	4		1	+	50
		30		10		-2		10
	2		3		1		5		30
		0		20		10		-3

Окончание табл. 4.3

	3		2	+	4		4	–	10
		+1		+3		-1		10
Потребности	30		30		10		20		90

Этот план проверяем на оптимальность. Снова находим по­тенциалы пунктов отправления и назначения. Для этого состав­ляем следующую систему уравнений:

Полагаем получаемДля каждой свободной клетки вычисляем число; имеем,

Таким образом, видим, что данный план перевозок не являет­ся оптимальным. Поэтому переходим к новому опорному плану (табл. 4.4).

Таблица 4.4

Пункты отправления	Пункты назначения								Запасы
	1		2		4		1		50
		30		0		-4		20
	2		3		1		5		30
		0		20		10		-3
	3		2		4		4		10
		-2		10		-4		-3
Потребности	30		30		10		20		90

Сравнивая разности новых потенциалов, отвечающих свободным клеткам табл. 4.4, с соответствующими числами, видим, что указанные разности потенциалов для всех свобод­ных клеток не превосходят соответствующих чисел. Следова­тельно, полученный план

является оптимальным. При данном плане стоимость перевозок