40-44Теория вероятностей

40. Формула доверительной вероятности при оценке генеральной доли признака. Средняя квадратическая ошибка повторной и бесповторной выборок и построение доверительного интервала для генеральной доли признака.

. теорема: вероятность того, что отклонение выборочной средней (или доли) от генеральной средней (или доли) не превзойдет число ∆>0, равна: Р(|ω-р|≤∆)=Ф(t)=γ, где t=∆/σ_ω. это формула доверительной вероятности для доли. Среднее квадратическое отклонение выборочной средней и выборочной доли собственно-случайной выборки называется средней квадратической ошибкой. а)повторная выборка: σ_ω=√pq/n ≈√ω(1-ω) /n (все под корнем и все делится на n). б) бесповторная выборка: σ ́΄_ω=√ω(1-ω) / n * (1-n/N)(все под корнем). Построение доверительного интервала. Для построения доверительных интервалов для параметров генеральных совокупностей могут быть реализованы два подхода, основанных на знании точного(при данном объеме выборки n) или асимптотического (при n→∞) распределения выборочных характеристик. Первый подход реализован далее при построении интервальных оценок параметров для малых выборок.

2-ой вариант ответа Вер-ть того что отклонение выборочной доли по абсолютной величине не превзойдет числа ,равна

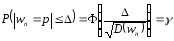
Где F-функция Лапласа, w-ген.доля p

Этот результат основывается на централ.пред.теор. В формуле D(w)есть неизв.пер. поэтому пользуемся приближ ф-ми. Сред.квад.ошибка

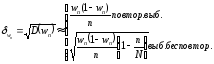
Доверит.интревал для доверит.доли может быть постр.по:

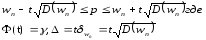
41 Формула доверительной вероятности при оценке генеральной средней. Средняя квадратическая ошибка повторной и бесповторной выборок и построение доверительного интервала для генеральной средней.

теорема: вероятность того, что отклонение выборочной средней (или доли) от генеральной средней (или доли) не превзойдет число ∆>0, равна: Р(|хвыб-х0|≤∆)=Ф(t)=γ, где t=∆/σ_х. это формула доверительной вероятности для средней. Среднее квадратическое отклонение выборочной средней и выборочной доли собственно-случайной выборки называется средней квадратической ошибкой. а)повторная выборка: σ_хвыб=√σ²/n≈√S²/n. б) бесповторная выборка: σ ́΄_хвыб^́=√S²/n(1-n/N)(все под корнем). Построение доверительного интервала. Для построения доверительных интервалов для параметров генеральных совокупностей могут быть реализованы два подхода, основанных на знании точного(при данном объеме выборки n) или асимптотического (при n→∞) распределения выборочных характеристик. Первый подход реализован далее при построении интервальных оценок параметров для малых выборок.

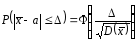2-ой вариант ответа Вер-ть того что отклон. ген. сред. от a не привзойдёт по апсол.вел.числа где Ф-лап.

Это резул.следств.цен..пред.т.

В формуле есть неизв. перем. ,поэтому пользуются приближ. Сред.квад.ош.:

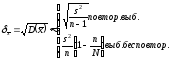
Доверит.интревал.надёжности γ для ген.сред.может быть найден:

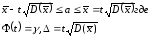
42. Определение необходимого объема повторной и бесповторной выборок при оценке генеральной средней и доли.

Для опред.n необход.задать надёжность оценки γ(дов.вер-ть) и точность Δ(пред.ош. выборки).

Для повтор.выб.при оценке ген. Сред.с надёжностью γ фор-ла для нах.объёма выборки имеет вид:

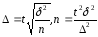
Где

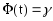
Для беспов.

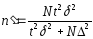
При оценке ген.доли для пов.выб.

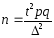
Беспов.

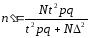
Если найден объём повтор выб. n то объём соответствующей беспов. по фор-ле: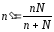

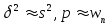
2ой вариант ответа для проведения выборочного наблюдения весьма важно правильно установить объем выборки n, который в значительной степени определяет необходимые при этом временные, трудовые и стоимостные затраты. Для определения n необходимо задать надежность (доверительную вероятность) оценки γ и точность (предельную ошибку выборки) ∆. 1. Для генеральной средней: а)повторная: n=t²*σ² /∆² ,б)бесповторная: n΄=N*t²*σ² / t²*σ² +N*∆². для для генеральной доли: а) повторная: n=t²pq /∆², б) бесповторная: n΄=N*t²pq / (t²pq + N∆²). Если найден объем повторной выборки n, то объем соответствующей бесповторной выборки n΄ можно определить по формуле: n΄= n*N /(n+N). Так как N /(n+N)<1, то при одних и тех же точности и надежности оценок объем бесповторной выборки n΄ всегда меньше объема повторной выборки n. на практике используется, в основном, бесповторная выборка.

43. Статистическая гипотеза и статистический критерий. Ошибки 1-го и 2-го рода. Уровень значимости и мощность критерия. Принцип практической уверенности.

статистической гипотезой называется любое предположение о виде или параметрах неизвестного закона распределения. Различают простую и сложную статистические гипотезы. Простая гипотеза в отличие от сложной, полностью определяет теоретическую функцию распределения СВ. проверяемую гипотезу обычно называют нулевой (или основной) и обозначают Н_0. правило, по которому гипотеза Н₀ отвергается или принимается, называется статистическим критерием или статистическим тестом. Множество возможных значений статистики критерия разбивается на 2 непересекающихся подмножества: критическую область (от области отклонения гипотезы ) W и область допустимых значений (область принятия гипотезы) не W. Вероятность α допустить ошибку первого рода, то есть отвергнуть гипотезу Н₀ , когда она верна называется уровнем значимости или размером критерия. Вероятность (1-β) не допустить ошибку второго рода, то есть отвергнуть гипотезу Н₀ , когда она не верна, называется мощностью (или функцией мощности) критерия. Вероятности ошибок первого и второго рода (α и β) однозначно определяются выбором критической области. При увеличении объема выборки возможно одновременное уменьшение вероятности α и β. Принцип практической уверенности: если вероятность события А в данном испытании очень мала, то при однократном выполнении испытания можно быть уверенным в том, что событие А не произойдет и в практической деятельности вести себя так, как будто событие А вообще невозможно. Он подтверждается практически. Например, отправляясь самолетом в другой город мы не рассчитываем на возможность погибнуть в авиакатастрофе, хотя некоторая вероятность такого события все же имеется.

44. Построение теоретического закона распределения по опытным данным. Понятие о критериях согласия.

.одна из важнейших задач мат. статистики – установление теоретического закона распределения СВ, характеризующей изучаемый признак по опытному распределению, представляющему вариационный ряд. Для решения этой задачи необходимо определить вид и параметры закона распределения. Предположение о виде закона распределения может быть выдвинуто исходя из теоретических предпосылок, опыта аналогичных предшествующих исследований и наконец на основании графического изображения эмпирического распределения. Параметры распределения неизвестны поэтому их заменяют наилучшими оценками по выборке. Между эмпирическими и теоретическими распределениями неизбежны расхождения. Тогда возникает вопрос: объясняются ли эти расхождения только случайными обстоятельствами, связанными с ограниченным числом наблюдений или они являются существенными и связаны с тем, что теоретический закон распределения подобран неудачно. Для ответа на этот вопрос и служат критерии согласия. Пусть необходимо проверить нулевую гипотезу Н₀ о том. Что исследуемая случайная величина Х подчиняется определенному закону распределения. Для проверки гипотезы Н₀ выбирают некоторую СВ U, характеризующую степень расхождения теоретического и эмпирического распределения, закон распределения которой при достаточно больших n известен и практически не зависит от закона распределения СВ Х. если СВ U приняла значение не меньше, чем фактически наблюдаемая в опыте u (U≥u), если Р (U≥u) =α мала, то гипотезу Н₀ отвергают. Но если Р (U≥u) =α не мала гипотезу Н₀ считают правдоподобной.