Примеры

1. Найти СДНФ и СКНФ для следующей функции:

x y | f

0 0 | 0

0 1 | 1

1 0 | 0

1 1 | 0

Решение.Воспользуемся разложениями (7) и (8):

f(x,y)=f(1,1)xyf(1,0)xy’f(0,1)x’yf(0,0)x’y’=

=0xy0xy’1x’y0x’y’= x’y,(СДНФ)

f(x,y)=(f(1,1)x’y’)(f(1,0)x’y)(f(0,1)xy’)(f(0,0)xy)=

=(0x’y’)(0x’y)(1xy’)(0xy)= )=(x’y’)(x’y)(xy). (СКНФ)

2. Построить СДНФ двойственной функции кf(x,y,z)=x’→yz.

Решение.СпособI. Воспользуемся определением двойственной формулы:

f^*(x,y,z)= f ’(x’,y’,z’)=(x’’→y’z’)’=(x→y’z’)’=(x’y’z’)’=

=x’’(y’z’)’=x(yz)=xyxz.

Способ II. Воспользуемся теоремой двойственности. Исключим тождественными преобразованиями импликацию:

f(x,y,z)=x’→yz=xyz.

Далее, заменим символы конъюнкции и дизъюнкции друг на друга:

f^*(x,y,z)=x(yz)=xyxz.

Вопросы и упражнения для самостоятельной работы

Построить СДНФ и СКНФ для функций f₁,f₂,f₃иf₄, заданных таблицей

xy z|f₁ f₂ f₃ f₄

0 0 0 | 0 1 1 1

0 0 1 | 0 0 1 1

0 1 0 | 1 1 0 1

0 1 1 | 1 1 0 1

1 0 0 | 1 0 1 1

1 0 1 | 1 0 0 1

1 1 0 | 1 1 0 1

1 1 1 | 1 0 0 1

Построить СДНФ и СКНФ для следующих функций:

а) xy, б)x↓y, в) (xy)↓z, г)x(yz), д)xyy’zx’z.

Построить двумя способами СКНФ и СДНФ двойственных функций f ^*для следующих функций:

а) xy, б)x↓y, в)xyг)xyz, д)x(yz).

§1.3. Важнейшие замкнутые классы булевых функций

Пусть K— некоторый класс (множество) булевых функций.Замыканием классаK называется множество всех тех функций, которые могут быть выражены через функции классаK. Замыкание классаK будем обозначать через [K]. Класс функций называетсязамкнутым, если он совпадает со своим замыканием, т.е . [K] = K.

Рассмотрим важнейшие замкнутые классы булевых функций.

Класс P₀. КлассP₀– этокласс всех функций, сохраняющих 0, то есть таких функцийf(x₁,x₂,…,x_n), для которыхf(0,0,…,0)=0.

КлассP₁. КлассP₁– этокласс всех функций, сохраняющих 1, то есть таких функцийf(x₁,x₂,…,x_n), для которыхf(1,1,…,1)=1.

КлассS. КлассS– этокласс всех самодвойственных функций, то есть таких функцийf, которые совпадают со своей двойственной функцией,f ^*=f.

КлассL. КлассL– этокласс всех линейных функций, то есть функций представимых в виде

f(x₁,x₂,…,x_n) = ₀₁x₁₂x₂…_nx_n,

где ₀,₁,₂, …,_n{0,1} – константы.

КлассM. КлассM– этокласс монотонных функций. Функцияf(x₁,x₂,…,x_n) называется монотонной, еслиf(₁,₂,…,_n)f(₁,₂,…,_n) при (₁,₂,…,_n)(₁,₂,…,_n).

Примеры

1. Проверить принадлежность каждому из классовP₀,P₁,S,L,Mфункцийи .

Решение.Выпишем соответствующие таблицы истинности:

x y |  

0 0 | 0 0

0 1 | 1 1

1 0 | 1 1

1 1 | 1 0

P₀: Из первой строки видно, что дизъюнкция и сложениесохраняют 0. Следовательно,,P₀;

P₁: Из последней строки видно, что дизъюнкция сохраняет 1, а сложение– нет. Следовательно,P₁, аP₁.

S: Для проверки принадлежности к классуSнеобходимо сравнить прямую и двойственную функции.

Способ I. Для дизъюнкции имеемf*=(xy)*= xy. Но

xy xy, следовательноS.

Способ II. Для сложениявоспользуемся таблицей:

xy|^*

0 0 | 0 1

0 1 | 1 0

1 0 | 1 0

1 1 | 0 1

Последний столбец для двойственной функции был получен по следующему правилу: столбец функции инвертируется (замены 01), полученные значения записываются в инвертированные строки. Например, строка 0 11 дляпревращается в строку 1 00 для^*.

Из полученной таблицы следует, что ^*, т.е.S.

L: Представим исследуемые функции через 1,и.

Для дизъюнкции имеем:

xy=(x’y’)’=((1x)(1y))’=1((1x)(1y))=

=1(1xyxy)= xyxy.

Здесь мы воспользовались законом де Моргана, тождеством x’=1x, дистрибутивностью сложенияотносительнои ассоциативностью(’’привычные’’ правила раскрытия скобок).

Полученное выражение содержит нелинейное слагаемое xy. Отсюда следует, чтоL.

Для сложения по модулю два имеем: f=xy– линейная функция. Значит,L.

M: Вернемся к таблицам истинности обеих функций (см. пунктP₀). Необходимо сравнить значения функции для каждой сравнимой пары аргументов. Мы видим, что дизъюнкция монотонна, а— не монотонна. Следовательно,M,M.

2.Найти линейную булеву функциюf(x,y,z), удовлетворяющую условиям:f(1,0,0)=1,f(0,1,0)=1,f(1,1,1)=0 иf(1,1,0)=0.

Решение.Будем искать линейную функцию в виде

f(x,y,z)=₀₁x₂y₃z.

Указанные условия приводят к системе линейных булевых уравнений

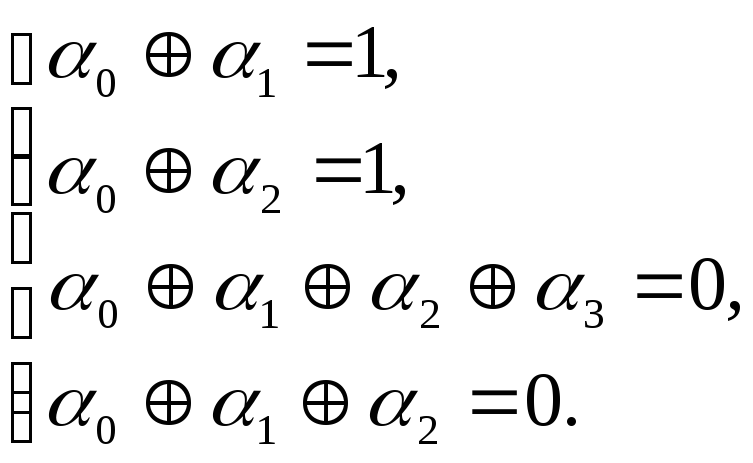
Воспользуемся методом Гаусса, учитывая, что 11=0:

.

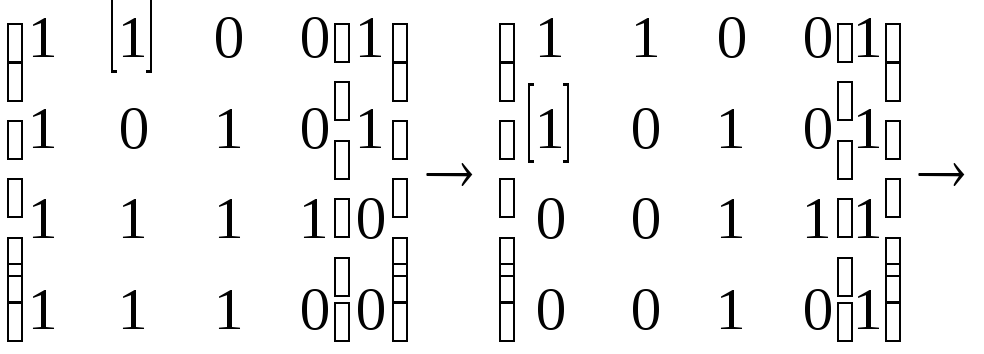
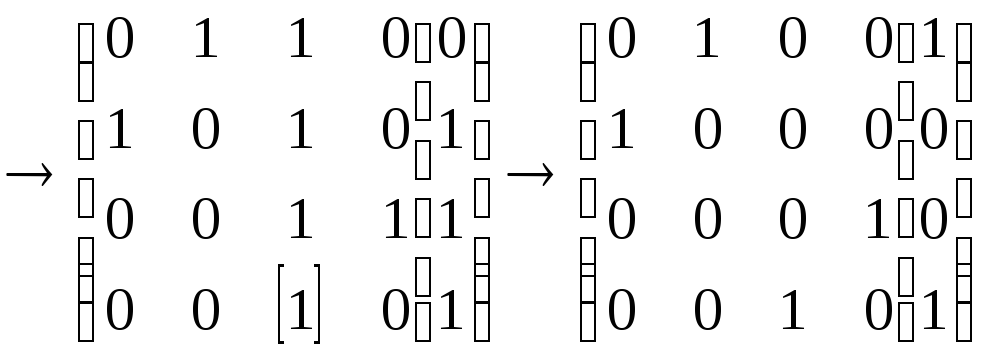Следовательно, ₀=0,₁=1,₂=1 и₃=0, т.е.f(x,y,z)=xy.