
- •Краткий конспект лекций по теории вероятностей Лекция1 Вероятность
- •Действия над событиями.
- •Классификация событий Событие, состоящее из всех элементарных событий, не содержащихся в а, обозначим и будем называть противоположным событием.
- •Полная группа событий – это совокупность n событий а1, а2, …, Аn, одно из которых обязательно произойдет, т.Е. Свойства операций над событиями
- •Правило двойственности (теорема де Моргана)
- •Алгебра событий.
- •Вероятность. Классическое определение вероятности события
- •Геометрическая вероятность
- •Статистическая вероятность
- •Свойства вероятности
- •Лекция 2 Условная вероятность.
- •Формула вероятности произведения событий (теорема умножения вероятностей). Независимые события
- •Формула вероятности суммы совместных событий (теорема сложения вероятностей)
- •Формула полной вероятности
- •Формула Байеса (теорема гипотез)
- •Лекция 3. Случайные величины
- •Лекция 4 Повторные испытания.
- •Распределения, связанные с повторными испытаниями.
- •Лекция 5
- •Лекция 6. Двумерные случайные величины
- •Свойства функции распределения.
- •Свойства плотности.
- •Свойства коэффициента корреляции.
- •Двумерное равномерное распределение
- •Двумерное нормальное распределение
- •Задача линейного прогноза.
- •Лекция 7. Законы больших чисел и центральная предельная теорема. Неравенства Чебышева.
- •Законы больших чисел.
- •Теорема Чебышева
- •Обобщенная теорема Чебышева.
- •Теорема Маркова.
- •Теорема Бернулли.
- •Предельные теоремы.
- •Теорема Ляпунова.
- •Теорема Леви – Линдеберга.
- •Интегральная теорема Муавра – Лапласа.
- •Лекция 8 Элементы математической статистики
- •Основные задачи статистики.
- •Эмпирические законы распределения.
- •Точечные оценки параметров распределения.
- •Требования к оценкам.
- •2. Несмещенная, состоятельная оценка дисперсии
- •Интервальные оценки.
- •Доверительные интервалы для параметров нормального закона распределения. Доверительный интервал для математического ожидания.
- •Доверительный интервал для среднеквадратического отклонения .
Точечные оценки параметров распределения.
Пусть неизвестен
параметр распределения![]() ,
любая функция
,
любая функция![]() на выборке
на выборке![]() называетсяточечной оценкой
называетсяточечной оценкой ![]() .
Оценки тоже являются случайными
величинами.
.
Оценки тоже являются случайными
величинами.
Требования к оценкам.
Несмещенность

Состоятельность
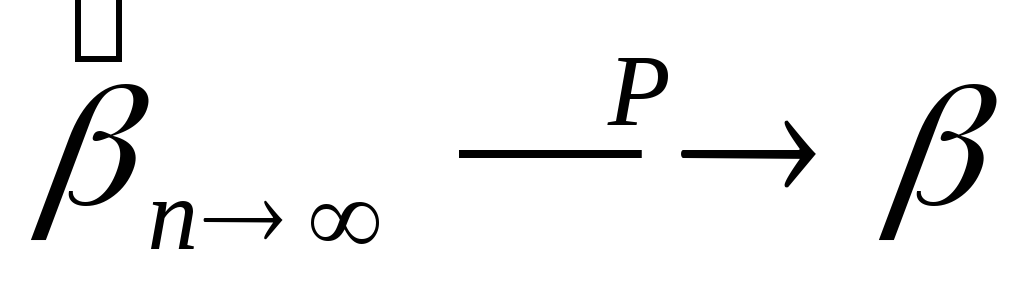
Эффективность (по сравнению с другими оценками) – если дисперсия оценки меньше дисперсий других оценок.
Можно показать,
что несмещенная оценка состоятельна,
если ее выборочная дисперсия стремится
к нулю при
![]() .
.
Оценки ищут различными методами: методом моментов, методом максимального правдоподобия, методом наименьших квадратов и др.
Оценка среднего
значения ГС (математического ожидания)
– выборочное среднее. ![]() .
.
Оценка несмещенная,т.к.![]() .
.
Оценка
состоятельная, т.к.
![]() по закону больших чисел.
по закону больших чисел.
Оценки дисперсии ГС:
Выборочная дисперсия

Это – смещенная, состоятельная оценка.
2. Несмещенная, состоятельная оценка дисперсии
Можно показать,
что
![]() .
.
Пример. Вычислим оценки для приведенного выше ряда распределения
-
xk
0
1
3
5
nk
5
2
1
2

1/2
1/5
1/10
1/5
![]() ,
,
![]() .
.
Интервальные оценки.
Доверительный
интервал– это интервал![]() ,
такой, что
,
такой, что![]() ,
,
где
![]() -доверительная вероятность.
-доверительная вероятность.
Общее правило
построения доверительного интервала
для любого параметра основано на
центральной предельной теореме, по
которой при больших n(n>50) оценка![]() имеет
нормальное распределение с
имеет
нормальное распределение с![]() ,
если
,
если![]() - несмещенная оценка, а функция
распределения случайной величины
- несмещенная оценка, а функция
распределения случайной величины![]() сходится по вероятности при
сходится по вероятности при![]() к функции стандартного нормального
распределения.
к функции стандартного нормального
распределения.
Квантиль![]() (уровня
(уровня
![]() ) случайной величиныXс
функцией распределенияF(x)
– это такое значение
) случайной величиныXс
функцией распределенияF(x)
– это такое значение
![]() случайной величиныX, что
случайной величиныX, что![]() .
.
|
|
Обозначим
|
стандартного
нормального распределения. По симметрии
плотности нормального распределения
![]() .
Так как
.
Так как![]() .
.
Так как
распределение случайной величины
![]() стремится к стандартному нормальному
распределению, то
стремится к стандартному нормальному
распределению, то![]() .
Отсюда получаемдоверительный интервал
.
Отсюда получаемдоверительный интервал
![]() .
.
Доверительные интервалы для параметров нормального закона распределения. Доверительный интервал для математического ожидания.
Если ГС имеет
нормальное распределение, то и любая
выборка распределена нормально. Известно,
что сумма нормальных случайных величин
тоже распределена нормально. Поэтому
оценка математического ожидания –
выборочное среднее – нормально
распределенная случайная величина с
![]() - известно.
- известно.
Поэтому, если
 известно,
то
известно,
то ,
идоверительный интервал дляматематического ожиданиястроится
так:
,
идоверительный интервал дляматематического ожиданиястроится
так:
![]() с доверительной вероятностью
с доверительной вероятностью![]() .
Квантили проще всего искать по таблицам
квантилей нормального распределения.
.
Квантили проще всего искать по таблицам
квантилей нормального распределения.
Если
 неизвестно,то нормированная случайная величина
неизвестно,то нормированная случайная величина (вместо
(вместо подставлена его оценкаs)
уже не распределена нормально.Она
имеет распределение Стъюдента с n-1
степенями свободы. Есть таблицы
квантилей распределения Стъюдента. По
доверительной вероятности
подставлена его оценкаs)
уже не распределена нормально.Она
имеет распределение Стъюдента с n-1
степенями свободы. Есть таблицы
квантилей распределения Стъюдента. По
доверительной вероятности определяют
определяют ,
по таблице квантилей определяют квантиль
,
по таблице квантилей определяют квантиль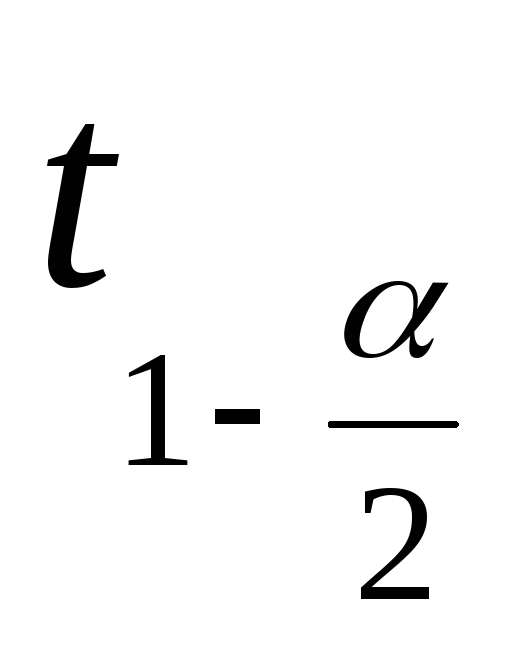 уровня
уровня .
Затем по той же схеме строятдоверительный
интервал для математического ожидания
.
Затем по той же схеме строятдоверительный
интервал для математического ожидания
 .
.
Если n> 20, то квантиль можно искать по таблицам квантилей нормального распределения.

