
- •Краткий конспект лекций по теории вероятностей Лекция1 Вероятность
- •Действия над событиями.
- •Классификация событий Событие, состоящее из всех элементарных событий, не содержащихся в а, обозначим и будем называть противоположным событием.
- •Полная группа событий – это совокупность n событий а1, а2, …, Аn, одно из которых обязательно произойдет, т.Е. Свойства операций над событиями
- •Правило двойственности (теорема де Моргана)
- •Алгебра событий.
- •Вероятность. Классическое определение вероятности события
- •Геометрическая вероятность
- •Статистическая вероятность
- •Свойства вероятности
- •Лекция 2 Условная вероятность.
- •Формула вероятности произведения событий (теорема умножения вероятностей). Независимые события
- •Формула вероятности суммы совместных событий (теорема сложения вероятностей)
- •Формула полной вероятности
- •Формула Байеса (теорема гипотез)
- •Лекция 3. Случайные величины
- •Лекция 4 Повторные испытания.
- •Распределения, связанные с повторными испытаниями.
- •Лекция 5
- •Лекция 6. Двумерные случайные величины
- •Свойства функции распределения.
- •Свойства плотности.
- •Свойства коэффициента корреляции.
- •Двумерное равномерное распределение
- •Двумерное нормальное распределение
- •Задача линейного прогноза.
- •Лекция 7. Законы больших чисел и центральная предельная теорема. Неравенства Чебышева.
- •Законы больших чисел.
- •Теорема Чебышева
- •Обобщенная теорема Чебышева.
- •Теорема Маркова.
- •Теорема Бернулли.
- •Предельные теоремы.
- •Теорема Ляпунова.
- •Теорема Леви – Линдеберга.
- •Интегральная теорема Муавра – Лапласа.
- •Лекция 8 Элементы математической статистики
- •Основные задачи статистики.
- •Эмпирические законы распределения.
- •Точечные оценки параметров распределения.
- •Требования к оценкам.
- •2. Несмещенная, состоятельная оценка дисперсии
- •Интервальные оценки.
- •Доверительные интервалы для параметров нормального закона распределения. Доверительный интервал для математического ожидания.
- •Доверительный интервал для среднеквадратического отклонения .
Свойства плотности.
 (функция распределения – неубывающая
функция).
(функция распределения – неубывающая
функция). (по свойству 5 функции распределения)
Справедливо обобщение
(по свойству 5 функции распределения)
Справедливо обобщение .
.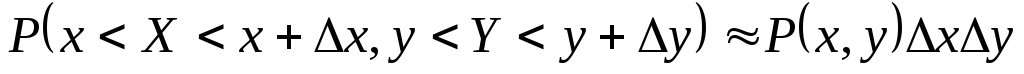
 (по свойству 4 функции распределения)
(по свойству 4 функции распределения)

 ,
, (Свойство 7 функции распределения)
(Свойство 7 функции распределения)
Независимость случайных величин.
Случайные
величины X,Yназываютсянезависимыми, если![]() ,
где
,
где![]() - функции распределения случайных
величинX,Y.
- функции распределения случайных
величинX,Y.
Если
случайные величины непрерывны, то,
дифференцируя это соотношение по x,y, получим![]() .
.
Соотношение
![]() поэтому можно считатьопределением
независимости непрерывных случайных
величин.
поэтому можно считатьопределением
независимости непрерывных случайных
величин.
Для
дискретных случайных величин
определение независимости можно
записать в виде![]() .
.
Математическое ожидание.
Математическим ожиданием функции двумерной случайной величины называется
![]() в дискретном случае,
в дискретном случае,
![]() в непрерывном случае.
в непрерывном случае.
Свойства математического ожидания
 (
( по условию нормировки)
по условию нормировки)
![]()
![]() =
=![]()
 для независимых случайных величин.
для независимых случайных величин.
![]()
![]()
![]()
![]() =
=![]() .
.
Ковариация (корреляционный момент).
Ковариациейслучайных величин называют![]() .
.
Свойства ковариации.
По свойству 1
![]()
Если X,Yнезависимы, то
 ,
(обратное неверно).
,
(обратное неверно).
Если случайные
величины независимы, то
![]() ,
тогда по свойству 1
,
тогда по свойству 1![]() .
.
Случайные
величины называются некоррелированными,если![]() ,из некоррелированности не следует
независимость,из независимости
следует некоррелированность.
,из некоррелированности не следует
независимость,из независимости
следует некоррелированность.
По свойству 1
![]() =
=![]() =
=![]() =
=![]()
Рассмотрим
случайную величину
![]() .
.![]()
![]()
![]()
![]() .
.
Заметим, что отсюда следует свойство дисперсии(приa=1)
![]() .
.
Так как
![]() ,
то
,
то![]()
![]() .
Это возможно только, если дискриминант
этого квадратного трехчлена относительноaменьше или равен нулю.
Выпишем это требование к дискриминанту:
.
Это возможно только, если дискриминант
этого квадратного трехчлена относительноaменьше или равен нулю.
Выпишем это требование к дискриминанту:
![]() .
Отсюда следует свойство 5.
.
Отсюда следует свойство 5.
Для того, чтобы случайные величины были линейно зависимы(Y=aX+b),необходимо и достаточно, чтобы

Необходимость.
Пусть Y=aX+b. Тогда![]()
![]()
![]() =
=![]()
Достаточность.
Пусть
![]() .Тогда (доказательство свойства 5)
.Тогда (доказательство свойства 5)![]() следовательно,z-
следовательно,z-![]() детерминированная
величина, т.е.
детерминированная
величина, т.е.![]() ,
поэтому величиныX,Y– линейно зависимы.
,
поэтому величиныX,Y– линейно зависимы.
Коэффициентом
корреляции называется![]() .
.
Свойства коэффициента корреляции.

Если X,Y– независимы, то



 тогда и только тогда, когдаX,Yлинейно зависимы.
тогда и только тогда, когдаX,Yлинейно зависимы.
Двумерное равномерное распределение
Случайный вектор (X,Y) равномерно распределен в областиD(площадьDравнаS), если его плотность распределения задана так:p(x,y) = 0, еслиxD,p(x,y) = 1/S, еслиxD.
Пример.Случайный вектор (X,Y) равномерно распределен в прямоугольнике 0xa, 0xb.
![]() ,
аналогично
,
аналогично
![]() .
.
![]() ,
аналогично
,
аналогично
![]() .
.
![]() ,
аналогично
,
аналогично
![]() .
.
![]()
![]()
Следовательно, случайные величины X,Yне коррелированны.
Двумерное нормальное распределение
Двумерная
случайная величина (X,Y)
распределена нормально со средними
значениямиm, m2,
дисперсиями![]() и коэффициентом корреляции
и коэффициентом корреляции![]() ,
если ее плотность задана:
,
если ее плотность задана:

Задача линейного прогноза.
Заданы
характеристики
![]() случайного вектора
случайного вектора![]() .
Вводится случайная величина – оценка
.
Вводится случайная величина – оценка![]() - линейный прогноз. Вычислить
- линейный прогноз. Вычислить![]() ,
чтобы линейный прогноз был наилучшим
среднеквадратическим (в смысле минимума
погрешности оценки:
,
чтобы линейный прогноз был наилучшим
среднеквадратическим (в смысле минимума
погрешности оценки:![]() ).
).
![]()
![]() .
.
За счет выбора
![]() можно лишь минимизировать последнее
слагаемое, сделав его нулем:
можно лишь минимизировать последнее
слагаемое, сделав его нулем:
![]() .Теперь
остается обеспечить минимум квадратного
трехчлена от
.Теперь
остается обеспечить минимум квадратного
трехчлена от![]() (найти
вершину параболы):
(найти
вершину параболы):
![]()
![]() .
Подставляя это значение, найдем
.
Подставляя это значение, найдем
![]() .
Вычислим погрешность оценки при этих
значениях параметров
.
Вычислим погрешность оценки при этих
значениях параметров
![]() .
.
При линейной
зависимости
![]() оценка точна, погрешность равна нулю.
оценка точна, погрешность равна нулю.
Чем меньше
коэффициент корреляции, тем грубее
оценка. В крайнем случае, при отсутствии
корреляции (![]() )
)![]() .
.
