№5лекция. ФЖиГ

№5 дәріс. Идеал сұйықтық қозғалысының ең қарапайым жағдайлары. Бернулли мен Коши интегралдары. Қалыптасқан құйынсыз қозғалысы. Торичелли формуласы. Газдардың кішкене тесіктен ағуы.

Қалыптасқан қозғалыс. Сұйықтықтың екі ең қарапайым жағдайларында идеал сұйықтық қозғалысының дифференциалдық теңдеулері интегралдарды береді: 1. қалыптасқан жағдайда және 2. құйынсыз қозғалыста.

Қалыптасқан қозғалыс жағдайын қарастырамыз. Бұл жағдайда қозғалыс режимі сұйықтықтың әр нүктесінде уақыт өткен сайын өзгермейді, және жылдамдық өрісі, құйын өрісі, гидродинамикалық қысымдар өрісі, массалық күштер өрісі тұрақты немесе стационар болады. Ток сызығы қалыптасқан қозғалыста бөлшектердің траекторияларымен сай келеді.

Негізгі қозғалыс теңдеуді ток сызығын жағалай сұйық бөлшектің элементар орын ауыстыруына скаляр көбейтіп, аламыз:

немесе

.

Қалыптасқан қозғалыста болғандықтан, өрнек толық ди фференциал болады және жазуға болады.

Бұл теңдеуді, екі шарт орындалған жағдайда оңай интегралдауға болады : 1) егер массалық күштердің потенциалы болса, оны арқылы белгілейік, сонымен

, ,

және 2) егер сұйықтық баротропты болса. Бұл жағдайда аламыз:

,

мұнда

(5.1)

және барлық дифференциалдар бөлшектің орын ауыстыру кезінде кейбір ток сызығын жағалай алынған, немесе басқаша айтканда

,

осыдан Бернулли деп аталатын, интегралды аламыз:

, (5.2)

мұнда берілген ток сызығында тұрақты мән сақтайтын, бірақта, жалпы айтқанда бір сызықтан басқа сызыққа өткенде өзгеретін шама болып табылады.

Егер массалық күштері ретінде ауырлық күштері болса, онда Оz өсін ветикаль жоғары бағыттап, аламыз: ,

және Бернулли интегралы түрінде болады.

Сығылмайтын сұйықтық үшін (5.1) формула бойынша аламыз:

.

-ға бөліп және белгі енгізіп, Бернулли интегралын тағы да мына түрде жазамыз:

. (5.3)

(5.3) теңдеудегі бірінші қосылғыш берілген ток түтікшеде қарастырып жатқан сұйық бөлшектің кейбір горизонталь бет үстінен биіктігін өрнектейді және геометриялық биіктік деп аталады. Екінші қосылғыш бастапқы жылдамдықпен жоғарыға лақтырылған материалдық нүктенің бостықта жоғары көтерілетін биіктігін өрнектейді, бұл қосылғыш жылдамдықтық биіктік деп аталады. Ақырында, үшінші қосылғыш, бағана түбіндегі қысым болатындай, тыныш қалпындағы сұйықтық бағанасының биіктігін өрнектейді; бұл қосылғыш пьезометриялық биіктік деп аталады.

Сонымен, Бернулли интегралы сығылмайтын сұйықтықтың қалыптасқан қозғалысында геометриялық, жылдамдықтық және пьезометриялық биіктіктердің қосындысы осы ток түтікшенің бөлшектері үшін өзгермей қалады екенін өрнектейді, бұл тағы да былай жазылуы мүмкін:

, (5.4)

Изотермиялық қозғалыста

,

сондықтан (5.2) Бернулли интегралы түріне келеді.

Құйынсыз қозғалыс. Егер қозғалыс уақытында сұйықтықтың жылдамдық өрісінің әр нүктесінде құйын болмаса, яғни және, демек жылдамдық потенциалды вектор болып табылады, сонымен , , , онда негізгі қозғалыс теңдеуі қарапайым түріне келеді:

. (5.5)

айқын болғандықтан, (5.5) теңдеуден аламыз

. (5.6)

Сығылмайтын сұйықтық үшін, өрістің барлық нүктесінде тұрақты болғандықтан, айқын қатыс орынды болады

, (5.7)

Сығылатын сұйықтық үшін сұйықтық баротропты болған жағдайда ұксас қатыс табуға болады. Бұл жағдайда белгі енгіземіз

немесе , (5.8)

сонда жазуға болады:

, (5.9)

себебі (5.8) – ден аламыз:

.

Дифференциалдардағы коэффициенттерді салыстырып, аламыз

; ; ,

бұдан (5.9) шығады; (5.7) теңдеуі (5.9)-дың дербес жағдайы болады.

Сонымен, құйынсыз қозғалыстың қарастырып жатқан жағдайларына (5.6) теңдеуі

,

түріне келеді, яғни осы жағдайларда массалық күштер потенциалды вектор болу керек. Күштердің потенциалын арқылы белгілеп, яғни , (5.6) қозғалыс теңдеуді

(5.10)

түрге келтіреміз. Соңғы теңдеу жақшалардың ішіндегі өрнек координаталарынан тәуелсіз және тек уақыттың функциясы екендігін көрсетеді:

, (5.11)

Қозғалыс теңдеулердің осы интегралы Коши интегралы деп аталады. Тек ауырлық күші болған жағдайда Коши интегралы

. (5.12)

түрге келеді.

Сығылмайтын сұйықтық үшін болады және Коши интегралы

. (5.13)

түрінде алынады.

Қалыптасқан құйынсыз қозғалысы. Торичелли формуласы. Газдардың кішкене тесіктен ағуы.

Қалыптасқан құйынсыз қозғалыста жылдамдықтар өрісі және қысым өрісі тұрақты (стационар) болады, сондықтан , кез келген функциясы кез келген С тұрақтыға айналады, және Коши интегралы

(5.14)

түріне келеді, мұнда .

Сығылмайтын сұйықтық жағдайда (5.1) теңдігі былай жазылады:

(5.15)

немесе -ға бөлгеннен кейін:

, (5.16)

мұнда ; біз Бернулли интегралымен түрі сай келетін теңдік аламыз. Соңғысынан айырмашылығы мынада болады: Бернулли интегралындағы тұрақтысы тек бір ток сызығында тұрақты болады, ал қалыптасқан құйынсыз қозғалыстағы интегралда С тұрақтысы қозғалыстағы сұйықтықтың барлық бөлшектерінде бір мән сақтайды. (5.14), (5.15), (5.16) интеграл түрі Бернулли – Эйлер интегралы деп аталады.

Жылдамдыққа қойылған шектеулер. Бернулли, Коши, Бернулли – Эйлер интегралдары болуы жылдамдықтың шамасына, қозғалыстағы сұйықтық тұтастықты үзілуге әкелмей одан аса алмайтын белгілі шек қояды. Мысалы, ауыр сығылмайтын сұйықтықтың қалыптасқан құйынсыз қозғалысын қарастырайық.

Өрістің биіктіктегі кейбір нүктесінде жылдамдық және қысым сәйкес тең болсын; сонда (5.16) интегралы

түрінде болады, осыдан .

Соңғы арақатыс шамасы, қысым идеал сұйықтықта теріс болмайтындықтан, сұйықтықтың ешбір нүктесінде мықты үлкен болмайтынын көрсетеді. Мысалы сол биіктіктегі нүктелерге теңсіздік алынады, бұдан жылдамдықтың шамасы үшін шек табамыз:

.

Егер, мысалы, үлкен ыдыста тұрған су тек атмосфералық қысым әсерінен бостыққа ағып жатса, онда ыдыстың бетіндегі шаманы нөлге жақын деп алуға болады және ағу жылдамдыққа шектеулік шарты алынады

.

Торичелли формуласы. Гидравликалық сұрақтарда Бернулли интегралының терең маңызы бар. Сығылмайтын ауыр сұйықтықтың үлкен ашық ыдыстан кішкене тесік арқылы ағу жылдамдығын анықтау үшін оны қолданамыз. Егер арқылы ыдыстағы еркін бет ауданың, арқылы тесіктің ауданың, және арқылы бет және тесіктегі жылдамдықтарды белгілесек, онда үзіксіздік теңдеуі береді:

.

Қозғалысты қалыптасқан және құйынсыз деп есептейік. Егер координаталар басын еркін бетінен алсақ және Оz өсін вертикаль төмен бағыттасақ, онда Бернулли – Эйлер интегралын қолданып, аламыз

, (5.17)

z тереңдіктегі тесікте қысым атмосфералық қысымға тең болғандықтан, мұнда ағып жатқан сұйықтық тағы да еркін бетін құрады. (5.17) теңдіктен аламыз немесе ,

осыдан .

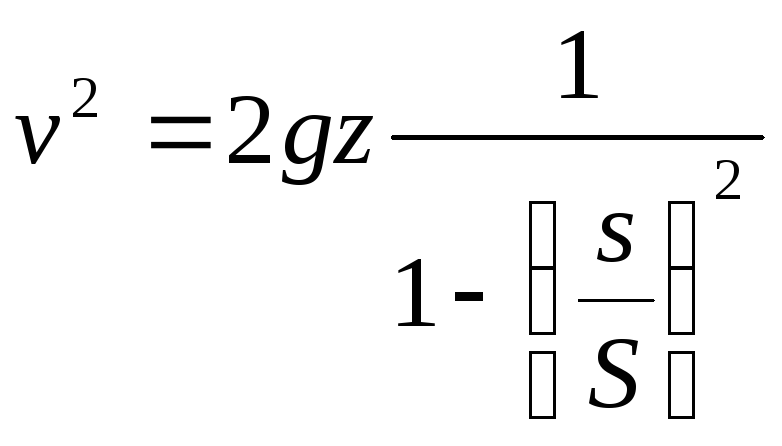Егер қатынасы кішкене болса, онда мүшесін ескермей, ағу жылдамдығы үшін жуық Торичелли формуласын аламыз

.

Газдардың кішкене тесіктен ағуы. Газдардың үлкен ыдыстан кішкене тесік арқылы ағу жылдамдығын бағалау үшін ұқсастық жуық формуласын алуға болады. Ыдыстағы газдың қысымы мен тығыздығы тең болсын, арқылы атмосфералық қысым және ауа тығыздықты белгілейік. Ағуды қалыптасқан және сонымен бірге құйынсыз қозғалыс ретінде қарастыруға және ыдыстың ішінде тесіктен жеткілікті қашықтықта газдың жылдамдығын ескермеуге болатындай, ыдыстың өлшемдерін жеткілікті үлкен деп есептейік.

Одан әрі тесіктен газдың ұлғаюы адиабаттық өтеді деп есептеп, ауырлық күшін ескермей және қоғалыс интегралын екі нүктеге – ыдыс ішіндегі жылдамдығы өте аз нүктеге және тесікке қолданып, аламыз

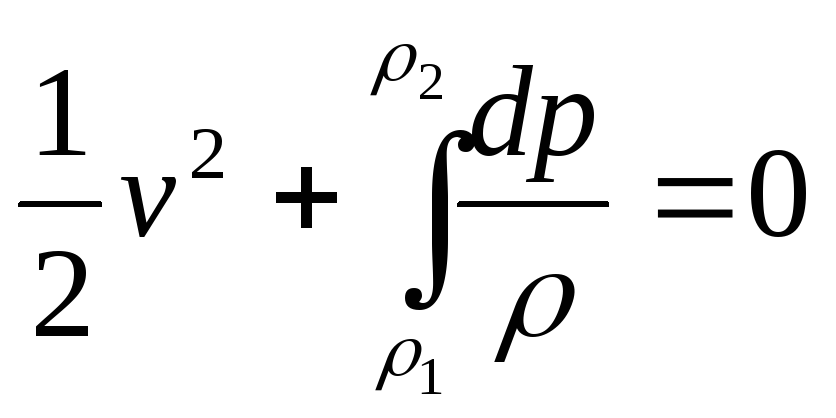, (5.18)

мұнда , .

(5.18) теңдеуден аламыз:

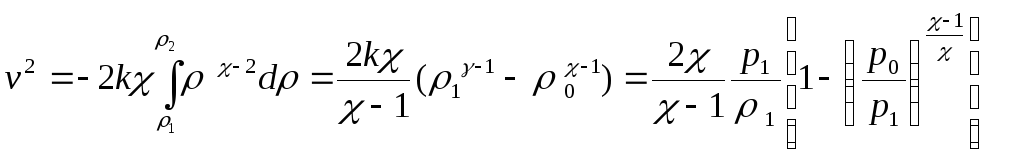
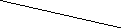
Жаттығу. Жінішке конусты түтікшеден газдың қалыптасқан құйылуында бөлшектердің траекториялары, конустың төбесінде жинақталатын, сызықтар болып табылады. Қозғалыс изотермиялы өтеді деп есептеп, АВ және аb, аудандары S пен s болатын, қималарындағы және жылдамдықтар арасындағы арақатысты табу керек (5.1).

A

a

v

S s

b

В

5.1 сурет. Жінішке конусты түтікшеден газдың ағу сұлбасы.

Шешім. Изотермиялық шарттан аламыз:

.

Ауырлық күшін ескермей және Бернулли – Эйлер интегралын

АВ және аb қималарына қолданып, аламыз

, (5.19)

мұнда және осы қималардағы қысымдар.

Үзіксіздік шарт береді:

,

бұдан және интеграл

немесе түріне келеді,

бұдан .