Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский национальный исследовательский технический университет им. А. Н. Туполева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Газизов Т.Р. КНИГА ЭлектромТерроризм

.pdf

Скачиваний:

Добавлен:

12.03.2015

Размер:

1.77 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 216 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

заряд располагается только на границах проводник–диэлектрик (свободный и поляризационный заряды) и на границах диэлектрик–диэлектрик (только поляризационный заряд) [61]. Обозначим плотность этого поверхностного за-

ряда за (r), где r – вектор положения в трёхмерной (x,y,z) Декартовой системе. Теперь допустим, что все эти границы дискретизированы (т.е. разбиты на подплощадки) процедурой, описанной в разделе 8.3. Пусть в результате дискретизации оказалось всего N подплощадок на J границах, N1 подплощадок на J1 границах проводник–диэлектрик и N2 подплощадок на J2 границах диэлектрик–диэлектрик, так что J=J1+J2 и N=N1+N2.

Потенциал (r) в точке r из-за заряда в точке r на всех границах и образа этого заряда относительно идеально проводящей плоскости в точке r€

	1		J
(r)			S j (r )G(r\|r ) da j ,	(8.1)
	4	0
			j 1

где Sj – площадь j-й границы; da j – дифференциальный элемент площади в точке r на Sj;

G(r\|r )	1	1		(8.2)
	r r		r r€

– функция Грина в свободном пространстве.

Вектор напряжённости электрического поля равен минус градиенту (r)

E(r) = – (r).

(8.3)

Подставляя (8.1) в (8.3) и полагая, что r находится не на поверхностях {Sj}, так что оператор можно внести под знак интеграла, получаем

					1				J
	E(r)				1			S j (r )H(r\|r ) da j ,											(8.4)
	E(r)		4				0	S j (r )H(r\|r ) da j ,											(8.4)
							0	j 1
где										r r			r r€
										r r			r r€
		H(r \| r )													.				(8.5)
										r	r	3	r r€	3
												3		3

Предел (8.4), когда r достигает границы Si, i=1…J, даёт
		1				J										(r)
E	(r)	1				S j (r )H(r\|r )da j n										(r)		,	(8.6)
E	(r)	4		0		S j (r )H(r\|r )da j n										2	0	,	(8.6)
				0		j 1											0

где n – единичный вектор нормальный к Si в точке r; E+ и E– – векторы напряжённости электрического поля на положительной (к которой указывает n) и отрицательной (от которой указывает n) сторонах Si.

На каждой i-й границе проводник–диэлектрик потенциал постоянный. Обозначая его за Vi, получаем для r на Si, i=1…J1

(r) = Vi .	(8.7)
	51

Подстановка (8.1) в (8.7) даёт

1		J
		S j (r )G(r \| r )da j Vi .	(8.8)
4	0
		j 1

Вектор смещения D(r) равен произведению диэлектрической проницаемости и вектора напряжённости электрического поля. Поскольку нормальная компонента D(r) на каждой границе диэлектрик–диэлектрик непрерывна, то для r на Si, i=(J1+1)…J, получаем

i J1 E (r) n i 1 J1 E (r) n ,

(8.9)

где i J1 и E+–диэлектрическая проницаемость и вектор напряжённости электрического поля, соответственно, на положительной стороне Si, а i 1 J1 и E–

– на отрицательной стороне Si. Подстановка (8.6) в (8.9) после деления на

( i J1 i 1 J1 ) даёт для r на Si, i=(J1+1)…J

i J1

i 1 J1

(r)

i J1

i 1 J1

S j

(8.10)

0 j 1

Уравнения (8.8) и (8.10) – система J интегральных уравнений с неизвестным общим зарядом (r) на границах Sj, j=1…J. Для приближённого численного решения эти уравнения сводятся методом моментов [61, 62] к системе N линейных алгебраических уравнений с N неизвестными n, n=1…N

N
Smn n Vi , m=1…N1,	(8.11)
n 1
N
Smn n 0 , m=(N1+1)…N.	(8.12)

n 1

Эта система решается NC раз (NC – число проводников в рассматриваемой системе) при потенциале Vi подплощадок проводник–диэлектрик на поверхности i-го проводника равном 1 В, а потенциале всех остальных подплощадок равном 0 В. (Вычисление Smn для (8.11) и (8.12) рассматривается в разделе 8.4). Наконец, вычисляются элементы ёмкостной матрицы [C]

	NL	n
Cij	i		n( j)an , i, j=1…NC ,

	n NFi	0

где an – площадь n-й подплощадки проводник–диэлектрик; n – диэлектрическая проницаемость со стороны n-й подплощадки проводник–диэлектрик; NFi и NLi – номера первой и последней подплощадок i-го проводника; i – ин-

декс для проводника, на котором суммируются заряды n(j); j – индекс для n, вычисленных при потенциале j-го проводника 1 В, а всех остальных – 0 В.

8.3. Дискретизация границ

Каждая граница проводник–диэлектрик и диэлектрик–диэлектрик рассматриваемой системы дискретизируется на прямоугольные подплощадки ортогональные осям X, Y, или Z и полностью описываемые следующими параметрами (используемыми далее с индексами n или m):

xn, yn, zn – координаты центра n-й подплощадки по x, y, z;

n – диэлектрическая проницаемость со стороны n-й подплощадки про- водник–диэлектрик;

m+ и m–– диэлектрические проницаемости на положительной и отрицательной сторонах m-й подплощадки диэлектрик–диэлектрик;

an – площадь, получаемая соответствующим произведением: xn zn,

xn yn, zn yn, где xn, yn, zn – размеры n-й подплощадки по x, y, z.

Вектор rm , соответствующий центру m-й подплощадки, в котором вычисляется поле, задаётся как

rm xxm yym zzm ,			(8.13)

где x, y и z – единичные векторы в направлениях x, y, и z, соответственно. Аналогично, вектор r n , соответствующий центру n-й подплощадки, по которой распределён заряд, создающий поле, и вектор r€n , соответствующий центру подплощадки, по которой распределён его образ, задаются как

r n xxn yyn zzn ,			(8.14)

r€ n xxn yyn zzn ,			(8.15)
где
xn xn t1 , yn yn t2 , zn zn t3 ,			(8.16)

где t1, t2, t3 – расстояния от центра n-й подплощадки в направлениях x, y, z.

8.4. Вывод окончательных формул для вычисления элементов Sm,n

После дискретизации можно вывести окончательные аналитические формулы для вычисления элементов Sm,n системы линейных уравнений (8.11) и (8.12), если рассматривать каждую ориентацию подплощадок отдельно.

Выражение для вычисления элементов Sm,n в (8.11), учитывая (8.8) с (8.2),

		1					€	m 1 N1
Smn	4 0					(Imn Imn ),						, где			(8.17)
	4 0							n 1 N
					1			€			1
Imn Sn			r			r		€	r		r€		da	.	(8.18)
Imn Sn			r	m		r	da ,	Imn Sn	r	m	r€		da	.	(8.18)
															53

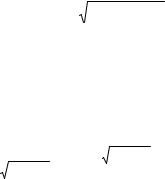
Выражения для вычисления элементов Sm,n в (8.12), учитывая (8.10) с (8.5),

			1					€	m = (N1 1)...N
	Smn				Imn Imn ,											,
	Smn			4 0	Imn Imn ,											,
				4 0					n = 1...N
	1									1
	1				€			m m		1
Smm	4 0	Imm Imm									2 0	, m = (N1				1)...N,
где	4 0							m m			2 0
где				rm r									rm r€
				rm r					€				rm r€
Imn Sn				rm r		3	nda , Imn Sn						rm r€	3	nda		.
Imn Sn				rm r		3	nda , Imn Sn						rm r€	3	nda		.

(8.19)

(8.20)

(8.21)

Следующий шаг – подстановка (8.13)–(8.15), с учётом (8.16), в (8.18) для подплощадок проводник–диэлектрик и в (8.21) для подплощадок диэлек- трик–диэлектрик. Окончательные формулы для этих случаев выводятся от-

дельно для каждой из трёх ориентаций подплощадок Sn: Y, Z, X.

8.4.1. Подплощадки проводник–диэлектрик
Для подплощадок Sn, ориентированных Y,		da dt1 dt3 ,	и формулы
(8.16) сводятся к
xn xn t1 , yn yn ,	zn zn t3 .		(8.22)

Imn в (8.18) после подстановки (8.13) и (8.14) с (8.22) и замены переменных

t1 (xm xn ) 1,

t3 (zm zn ) 2

принимает вид

d 1

Imn d 2

где

(xm xn ), a2

(xm xn ),

), c y

В (8.24) интеграл по d 1 является стандартным

, a 0

ln x

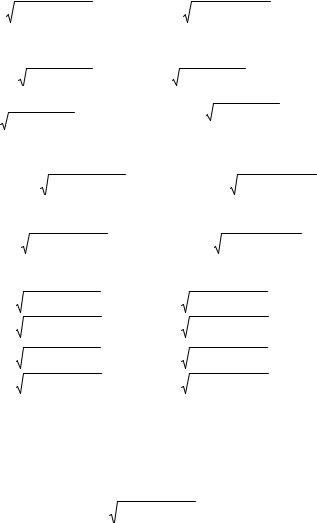
и даёт

(8.23)

(8.24)

(8.25)

(8.26)

			b1										2				2						2							b1													2					2					2
													2				2				2		2																				2					2					2						(8.27)
		Imn ln a1										a1			c1						2			d 2 ln a2																a2				c1						2					d 2.				(8.27)
			b2																											b2
В (8.27) интеграл по d 2 после долгих выкладок берётся аналитически
													a		2	c			2			x	2																a	2		c		2		x			2
					ln a								a			c						x		dx				x ln a											a			c				x

												2				2						2																							a	2		c			2	x			2
												2				2						2												x a											a			c				x
		a ln x									a		c				x					x 2c arctg																																				,
		a ln x									a		c				x					x 2c arctg																								c												,
																																														c

давая окончательное аналитическое выражение
						b				a			1				a		2			b 2 c						2										b			a			2					a		2 b						2 c 2
I	mn	2c	arctg					1					1				1						1			1				arctg									1					2							2				1				1
I		2c	arctg																											arctg
		1															c1																																	c1
																	c1																																	c1

			b	2		a			1					a		2	b					2 c			2								b					2	a		2		a					2 b					2		c 2
				2					1						1							2		1														2			2							2					2				1
		arctg																										arctg
		arctg													c													arctg																			c
															c																																c
															1																																	1

					b								a		2	b					2 c			2								b								a		2	2	b				2	c				2
								1						1					1				1													1						2					1					1
		a1 ln																								a2 ln
		a1 ln											a		2	b						2 c		2		a2 ln														a			2	b				2		c			2
					b			2					a		2	b				2		2 c		2								b			2					a		2	2	b				2		c			2
								2						1						2			1												2							2						2				1
					a			1					a		2	b					2 c			2								a				1				a		2 b						2	c				2
								1						1					1				1													1						1					2					1
		b1 ln																								b2 ln																													.				(8.28)
		b1 ln											a		2 b							2 c				b2 ln														a				b						c					.				(8.28)
					a			2					a		2 b							2 c		2								a			2					a		2	2	b				2		c			2
								2						2						1			1												2							2						2				1
€		в (8.18) после подстановки (8.13) и (8.15) с (8.22) и замены переменных
Imn
											t1 (xm xn ) 1,																			t3 (zm zn ) 2																													(8.29)
принимает вид
																						d1		a1								d 1
															€							d 2										d 1
															Imn							d 2							2					2						2		,																	(8.30)
																						d2		a2				1 2									c2
где					xn																							xn
			a1		xn						(xm xn ), a2																	xn				(xm xn ),
			a1								(xm xn ), a2																					(xm xn ),																											(8.31)
							2																						2
			d			zn					(z					z					), d						zn				(z							z			), c					y						y				.
						zn								m				n					2				zn							m						n					2					m				n

			1				2																					2
							2																					2
																																																												55

€
Видно, что (8.30) имеет вид (8.24), и Imn можно вычислить по (8.28) для
Imn , подставляя c2 вместо c1, d1 вместо b1, d2 вместо b2 и (8.31).
Для подплощадок Sn, ориентированных Z, da dt1 dt2 ,	и формулы
(8.16) сводятся к
xn xn t1 , yn yn t2 , zn zn .	(8.32)

Imn в (8.18) после подстановки (8.13) и (8.14) с (8.32) и замены переменных

t1 (xm xn ) 1,

(ym yn ) 2

(8.33)

совпадает с (8.24), где

(xm xn ), a2

(xm xn ),

(8.34)

), b

), c z

€

Очевидно, что Imn

можно вычислить по (8.28), но подставляя (8.34).

Imn в

(8.18) после подстановки (8.13) и (8.15) с (8.32) и замены переменных

t1 (xm xn ) 1,

(ym yn ) 2

(8.35)

принимает вид (8.24), где

(xm xn ), a2

(xm xn ),

(8.36)

(ym yn ), d2

(ym yn ), c2 zm zn .

€

Очевидно,

что

можно вычислить по (8.28)

для Imn ,

подставляя c2

Imn

вместо c1, d1 вместо b1, d2 вместо b2 и (8.36).

da dt2

Для подплощадок Sn, ориентированных X,

dt3 ,

и формулы

(8.16) сводятся к

xn , yn

yn t2

, zn

zn t3 .

(8.37)

Imn в (8.18) после подстановки (8.13) и (8.14) с (8.37) и замены переменных

t3 (zm zn ) 1, t2 (ym yn ) 2 (8.38)

совпадает с (8.24), где

(zm zn ), a2

(zm zn ),

), b

), c x

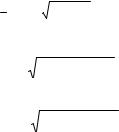
Очевидно, что Imn можно вычислить по (8.28), но подставляя (8.39). (8.18) после подстановки (8.13) и (8.15) с (8.37) и замены переменных

(8.39)

€

Imn в

t3 (zm zn ) 1,

t2 (ym yn ) 2

(8.40)

принимает вид (8.24), где

(zm zn ), a2

(zm zn ),

(8.41)

), d

), c

€

Очевидно, что Imn можно вычислить по (8.28) для Imn , подставляя c2 вместо c1, d1 вместо b1, d2 вместо b2 и (8.41).

8.4.2. Подплощадки диэлектрик–диэлектрик

Вывод формул для подплощадок диэлектрик–диэлектрик аналогичен выводу для подплощадок проводник–диэлектрик. Для обоих выражения для замены переменных и пределов интегрирования оказываются одинаковыми.

Подплощадки диэлектрик–диэлектрик Y

В этом случае рассматривается электрическое поле в подплощадках ди- электрик–диэлектрик ортогональных оси Y (пронумерованных с N1+1 по NY). Поэтому, в интегралах (8.21) подставляется y вместо n, и в числителях этих интегралов остаётся только координатаY.

Для подплощадок Sn, ориентированных Y, Imn в (8.21) после подстановки (8.13) и (8.14) с (8.22) и замены переменных (8.23) принимает вид

b	a		c1d 1
Imn 1 d 2 1			c1d 1						,	(8.42)
Imn 1 d 2 1								3	,	(8.42)
b2	a2	2	2	2	c1	2	2
		1	2		c1

где все константы задаются (8.25).

Интеграл по d 1 в (8.42) берётся по формуле 1.2.43.17 [63]

			dx				1					x		, давая			(8.43)
						3	2							, давая			(8.43)
	x	2	a		2		a				x2 a2
		2			2	2	a				x2 a2
	b1							c1a1
Imn								c1a1							d 2
Imn			2			2			2			2		2	d 2
	b2		2			c1			2			c1	a1
		b1							c1a2
									c1a2							d 2.	(8.44)
					2	2			2			2		2		d 2.	(8.44)
		b2		2		c1				2		c1	a2

Интеграл по d 2 в (8.44) берётся по формуле 1.2.45.11 [63]

						dx										1								a		2	b			2				2			2
						dx										1					x			a			b							2	b		2
																			arctg												, a							,
	x	2	b		2	x	2	a		2			b a			2	b	2	arctg							2		a		2	, a							,
	x		b			x		a					b a				b				b x							a
давая окончательную аналитическую формулу для Imn
							a1b1															a1b2
							a1b1															a1b2
arctg															arctg
arctg							b 2 c 2								arctg					a	2		b			2		c		2
			c a 2				b 2 c 2											c		a	2		b			2		c		2
			1			1			1			1							1	1					2					1
																																			c1 0,
									a2b1															a2b2											c1 0,
									a2b1															a2b2													0,
arctg																	arctg																,		a1
arctg								2			2			2			arctg						2					2			2		,		a1
							2	2	b1		2			2									2					2			2				a		0;
				c1 a			2		b1			c1							c1 a				2	b2					c1						a		0;
																																				2
																																			c1 0,
									a2b1															a2b2											c1 0,				(8.45)
Imn arctg									a2b1								arctg							a2b2									,		a		0,		(8.45)
Imn arctg																	arctg																,		a		0,
								2	b		2 c 2										a		2	b				2	c 2							1
				c a			2	2	b		2 c 2								c	1	a		2	b				2	c 2							a	0;
						1	2			1				1						1			2					2			1					a	0;
																																				2
																																	c1			0,
							a1b1															a1b2											c1			0,
							a1b1															a1b2
arctg															arctg																	,	a1 0,
arctg							b 2 c 2								arctg																	,	a1 0,
			c a 2				b 2 c 2											c		a	2		b			2		c		2							0;
			1			1			1			1							1	1					2					1				a	2		0;
																																			2
			0, a1 0, a2 0;
0, c1			0, a1 0, a2 0;
0, c			0.
		1

€

Imn в (8.21) после подстановки (8.13) и (8.15) с (8.22) и после замены пе-

ременных (8.29) принимает вид (8.42) и может быть вычислен по (8.45) для Imn , подставляя c2 вместо c1, d1 вместо b1, d2 вместо b2 и (8.31).

Для подплощадок Sn, ориентированных Z, Imn в (8.21) после подстановки (8.13) и (8.14) с (8.32) и замены переменных (8.33) принимает вид

b1	a1		2d 1
Imn d 2			2d 1						,	(8.46)
Imn d 2		2	2	2	c1	2		3	,	(8.46)
b2	a2	2		2		2	2
		1

где все константы задаются (8.34).

Интеграл по d 1 в (8.46) берётся по (8.43), давая

b1				2a1
Imn				2a1				d 2
Imn	2		2		2	2	2	d 2
b2	2		c1		2	c1	a1
b1				2a2
				2a2					d 2.	(8.47)
	2		2		2	2	2		d 2.	(8.47)
b2		2	c1		2	c1	a2

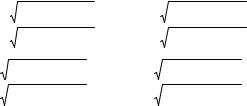
Интеграл по d 2 в (8.47) преобразуется к виду

dx	1		x a		, a 0,

		ln
x2 a2	2a			x a

давая окончательную аналитическую формулу для Imn

Imn		1	ln		a1 a12			b12 c12					1	ln		a1	a12 b2			2 c12
		2			a1	a1	2	b1	2	c1	2		2			a1	a1	2	2		c1	2
																		b2
	1	ln		a2 a22 b12 c12								1	ln		a2		a22 b2		2 c12				.	(8.48)

	2			a2		2		2		2		2			a2		2	b2	2		2

						a2	b1		c1								a2			c1

€

Imn в (8.21) после подстановки (8.13) и (8.15) с (8.32) и замены переменных (8.35) принимает вид

d1	a1		2d 1
€			2d 1
Imn d 2		2	2	2	c2	2		3	,	(8.49)
d2	a2	2		2		2	2
		1

где все константы задаются (8.36). Из сравнения (8.49) с (8.46) видно, что

€

Imn можно вычислить по (8.48) для Imn , изменив знак, подставив c2 вместо

c1, d1 вместо b1, d2 вместо b2 и подставив (8.36).

Для подплощадок Sn, ориентированных X, Imn в (8.21) после подста-

новки (8.13) и (8.14) с (8.37) и после замены переменных (8.38) принимает вид (8.46), где все константы задаются (8.39). Очевидно, этот интеграл можно вычислить по (8.48), но подставляя (8.39).

€

Imn в (8.21) после подстановки (8.13) и (8.15) с (8.37) и замены перемен-

ных (8.40) принимает вид (8.49), где все константы задаются (8.41). Из сравнения (8.49) с (8.46) видно, что (8.49) можно вычислить по (8.48) для Imn ,

изменив знак, подставив c2 вместо c1, d1 вместо b1, d2 вместо b2, и (8.41).

Подплощадки диэлектрик–диэлектрик Z

В этом случае рассматривается электрическое поле в подплощадках ди- электрик–диэлектрик ортогональных оси Z (пронумерованных с NY+1 по NZ). Поэтому, в интегралах (8.21) подставляется z вместо n, и в числителях этих интегралов остаётся только координата Z.

Для подплощадок Sn, ориентированных Y, Imn в (8.21) после подстановки (8.13) и (8.14) с (8.22) и замены переменных (8.23) принимает вид,

€

совпадающий с (8.46), и вычисляется по (8.48) с подстановкой (8.25). Imn в (8.21) после подстановки (8.13) и (8.15) с (8.22) и замены переменных (8.29)

принимает вид (8.46) и вычисляется по (8.48) для Imn , подставляя c2 вместо

c1, d1 вместо b1, d2 вместо b2 и подставляя (8.31).

Для подплощадок Sn, ориентированных Z, Imn в (8.21) после подстановки (8.13) и (8.14) с (8.32) и замены переменных (8.33) принимает вид,

€

совпадающий с (8.42) и вычисляется по (8.45) с подстановкой (8.34). Imn в

(8.21) после подстановки (8.13) и (8.15) с (8.32) и замены переменных (8.35) принимает вид (8.42) и вычисляется по (8.45) для Imn , подставляя c2 вместо

c1, d1 вместо b1, d2 вместо b2 и подставляя (8.36).

Для подплощадок Sn, ориентированных X, Imn в (8.21) после подста-

новки (8.13) и (8.14) с (8.37) и замены переменных (8.38) принимает вид (8.46), где все константы задаются (8.39). Видно, что он вычислим по (8.48),

€

но с подстановкой (8.39). Imn в (8.21) после подстановки (8.13) и (8.15) с

(8.37) и замены переменных (8.40) принимает вид (8.46) и вычисляется по (8.48) для Imn , подставляя c2 вместо c1, d1 вместо b1, d2 вместо b2 и (8.41).

Подплощадки диэлектрик–диэлектрик X

В этом случае рассматривается электрическое поле в подплощадках ди- электрик–диэлектрик ортогональных оси X (пронумерованных с NZ+1 по N). Поэтому, в интегралах (8.21) подставляется x вместо n, и в числителях этих интегралов остаётся только координата X.

b1	a1		1d 1
Imn d 2			1d 1						,	(8.50)
Imn d 2		2	2	2	c1	2		3	,	(8.50)
b2	a2	2		2		2	2
		1

где все константы задаются (8.25).

Интеграл по d 1 в (8.50) берётся по формуле 1.2.43.18 [3]

		xdx				1		, давая
	x2	a2 3/ 2				x2 a2
b1			d 2			b1			d 2
Imn											.	(8.51)
		2	2	a1	2		2	2	2	2
b2		2	c1			b2			c1	a2

Интеграл по d 2 в (8.51) стандартный (8.26), и окончательная аналитическая формула для Imn

		b	2	a	2 b	2	c 2	b		a	2	2 b	2	c 2
I		ln		1		2	1		1			1		1	.	(8.52)

	mn			a	2 b	2	c 2	b		a		2 b	2	c 2
		b							2		2
			1	1	1		1						2	1

<<< < Предыдущая 1 2 3 4 56 / 216 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.03.2015421.89 Кб11Вторая Ливанская война- конфликт.doc
#
12.03.2015407.55 Кб4вывод 13 лист.doc
#
12.03.20153.07 Mб48Высшая математика.docx
#
14.11.20181.41 Mб31Г л а в а 3(фопи).doc
#
21.12.20181.36 Mб10Г О Т О В Ы Й К У Р С О В И К.doc
#
12.03.20151.77 Mб92Газизов Т.Р. КНИГА ЭлектромТерроризм.pdf
#
12.03.201510.82 Кб16ГАЗОТУРБИННАЯ УСТАНОВКА.rtf
#
30.10.2018188.42 Кб4генплан-Мавлютов.doc
#
11.09.2019990.24 Кб8Геометрическое приложение определённого интегра...rtf
#
12.03.2015209.41 Кб15Гидрология мет 2007 - копия на печать.doc
#
12.03.201517 Mб149Гизатуллин монография 1.pdf