Двойственный симплекс-метод
Двойственный симплекс-метод является методом, при котором сначала симплексным методом решается исходная задача, а затем оптимальное решение двойственной задачи находится с помощью теорем двойственности.
Пример. Составить и решить задачу, двойственную следующей задаче:
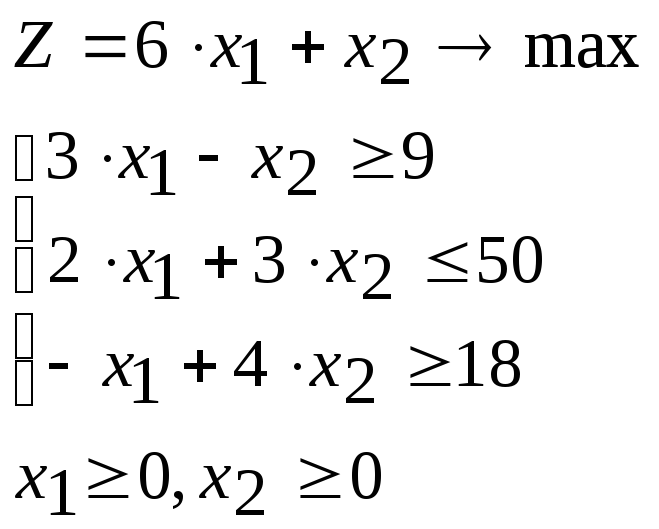
Решение.
Сформулируем задачу, двойственную для исходной задачи.
Поскольку исходная задача является задачей на отыскание максимума целевой функции, то для составления двойственной задачи, первоначально необходимо все ограничения-неравенства исходной задачи привести к виду, когда они имеют знак «≤». Для этого обе части неравенств со знаком «≥» умножим на (-1).
Тогда двойственная задача (задача минимизации целевой функции при ограничениях-неравенствах со знаком «≥») будет иметь вид:
Исходная задача линейного программирования
Двойственная задача линейного программирования
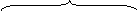
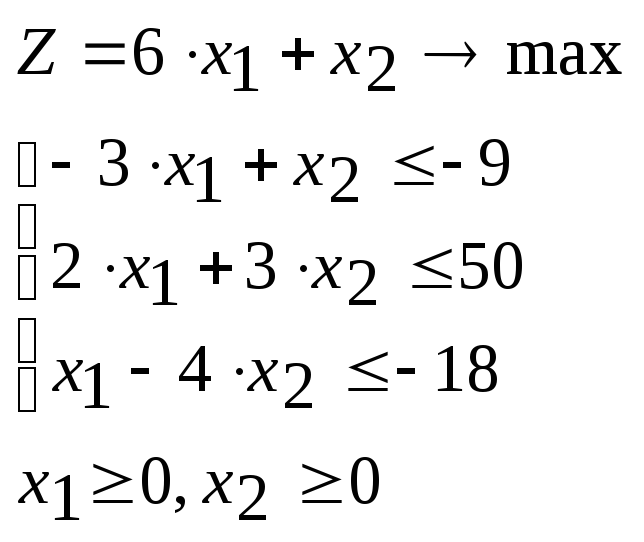
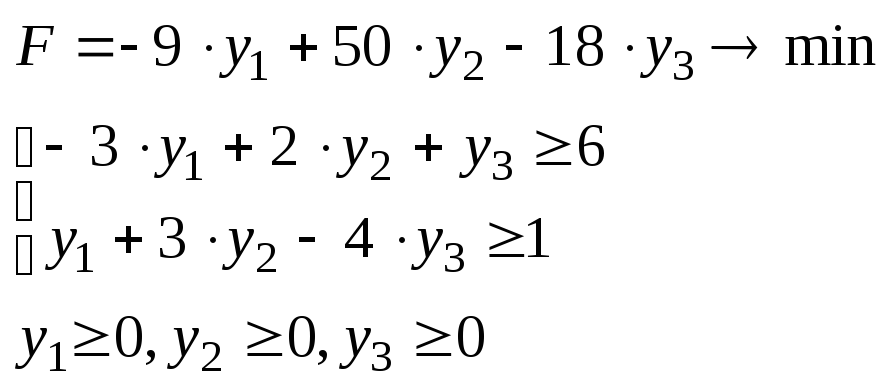
Используя теоремы двойственности, можно не решая двойственную задачу симплексным методом, на основе последней симплекс-таблицы оптимального решения исходной задачи получить последнюю симплекс-таблицу оптимального решения двойственной задачи.
В результате решения исходной задачи линейного программирования симплексным методом следующую симплекс-таблицу соответствующую оптимальному решению (см. Таб.3.).
Согласно
первой теореме двойственности, если
одна из взаимно двойственных задач
имеет оптимальное решение, то его имеет
и другая задача, причем оптимальные
значения их функций равны:
.
Установим соответствие между переменными исходной и двойственной задач (базисным переменным одной задачи соответствуют свободные переменные другой, и наоборот):
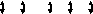
Положительным компонентам оптимального решения одной из взаимно двойственных задач соответствуют нулевые компоненты оптимального решения другой задачи.
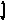
Подставив
найденные значения
в целевую функциюF,
получим
,
что и подтверждается первой теоремой
двойственности.
Составим последнюю симплекс-таблицу оптимального решения двойственной задачи по следующим правилам:
Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных целевой функции задачи, выраженной через свободные переменные её оптимального решения;
Матрица коэффициентов свободных переменных симплекс-таблицы оптимального решения двойственной задачи (кроме строки целевой функции) получается путем транспонирования матрицы коэффициентов свободных переменных симплекс-таблицы оптимального решения исходной задачи с противоположными знаками;
Коэффициенты при свободных переменных в строке целевой функции в симплекс-таблице оптимального решения двойственной задачи равны соответствующим свободным членам симплекс-таблицы оптимального решения исходной задачи (с противоположным знаком, если исходная задача является задачей максимизации).
В результате последняя симплекс-таблица оптимального решения двойственной задачи будет иметь вид:
|
Базисные переменные |
Свободные члены |
Свободные переменные | ||
|
y4 |
y1 |
y5 | ||
|
y2 |
|
|
-1 |
|
|
y3 |
|
|
-1 |
|
|
F |
|
|
-23 |
|
при
.