Оглавление

Оглавление 1

Введение 2

1 Постановка задачи 3

2 Описание метода 3

3 Алгоритм решения 4

4 код программы 9

5 Контрольный пример для отладки 9

7 Инструкция 12

8 Заключение. 13

9 Список использованной литературы: 13

Приложение А 14

Код программы. 14

Введение

Решение систем линейных алгебраических уравнений - одна из основных задач вычислительной линейной алгебры. Методы решения систем линейных уравнений широко используются в задачах математики, экономики, физики, химии и других науках. На практике, они позволяют не делать лишних действий, а записать систему уравнений в более компактной форме и сократить время выполнения задач. Поэтому, будущим специалистам очень важно понять основные методы решения и научиться выбирать оптимальный.

Хотя задача решения системы линейных уравнений сравнительно редко представляет самостоятельный интерес для приложений, от умения эффективно решать такие системы часто зависит сама возможность математического моделирования самых разных процессов с применением ЭВМ.

1 Постановка задачи

Дано: Система линейных алгебраических уравнений.

Требуется решить систему линейных алгебраических уравнений с вещественными коэффициентами с помощью метода Гаусса.

2 Описание метода

Существует множество методов решения систем линейных алгебраических уравнений таких как: метод Крамера, решение СЛАУ матричным методом, метод Гаусса.

Метод Гаусса - классический метод решения системы линейных алгебраических уравнений (СЛАУ). Состоит в постепенном понижении порядка системы и исключении неизвестных.

Достойнства метода:

-Менее трудоемкий по сравнению с другими методами

-Позволяет однозначно установить, совместна система или нет, и если совместна найти ее решение

-Позволяет найти максимальное число линейно независимых уравнений-ранг матрицы системы.

Существенные Недостатки: этот метод не позволяет найти общие формулы, выражающие решение системы через ее коэффициенты и свободные члены, которые необходимо иметь при теоретическом иследовании.

Суть метода Гаусса состоит в последовательном исключении неизвестных переменных: сначала исключается X1 из всех уравнений системы, начина со второго, далее исключается X2 из всех уравнений, начиная с третьего, и так далее, пока в последнем уравнении останется только неизвестная переменная Хn.Такой процесс преобразования уравнений системы для последовательного исключения неизвестных переменных называется прямым ходом метод Гаусса. После завершения прямого хода метода Гаусса из последнего уравнения находится Хn, с помощью этого значения из предпоследнего уравнения вычисляется Xn-1,и так далее, из первого находится Х1. Процесс вычисления неизвестных переменных при движении от последнего уравнения системы к первому называется обратным ходом метода Гаусса.

3 Алгоритм решения

1.Кратко опишем алгоритм исключения неизвестных переменных.

Будем считать, что , так как мы всегда можем этого добиться перестановкой местами уравнений системы. Исключим неизвестную переменную x₁ из всех уравнений системы, начиная со второго. Для этого ко второму уравнению системы прибавим первое, умноженное на - , к третьему уравнению прибавим первое, умноженное на , и так далее, к n-омууравнению прибавим первое, умноженное на . Система уравнений после таких преобразований примет вид

 

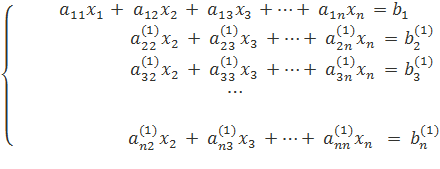
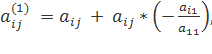
где   .

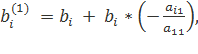
К такому же результату мы бы пришли, если бы выразили x₁ через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменная x₁ исключена из всех уравнений, начиная со второго.

2.Далее действуем аналогично, но лишь с частью полученной системы, которая отмечена на рисунке

 

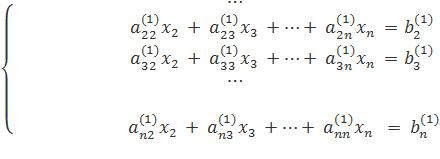
Будем считать, что  (в противном случае мы переставим местами вторую строку с k-ой, где ). Приступаем к исключению неизвестной переменной x₂ из всех уравнений, начиная с третьего.

Для этого к третьему уравнению системы прибавим второе, умноженное на , к четвертому уравнению прибавим второе, умноженное на , и так далее, к n-омууравнению прибавим второе, умноженное на . Система уравнений после таких преобразований примет вид

 

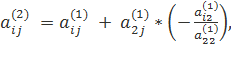
где   .

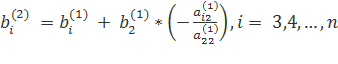Таким образом, переменная x₂ исключена из всех уравнений, начиная с третьего.

Далее приступаем к исключению неизвестной x₃, при этом действуем аналогично с отмеченной на рисунке частью системы

 

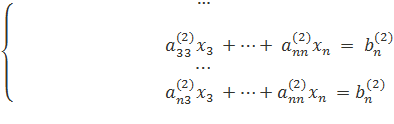
Так продолжаем прямой ход метода Гаусса пока система не примет вид

 

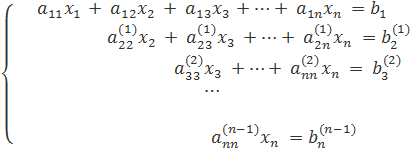
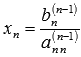
С этого момента начинаем обратный ход метода Гаусса: вычисляем x_n из последнего уравнения как , с помощью полученного значения x_n находим x_n-1 из предпоследнего уравнения, и так далее, находим x₁ из первого уравнения.

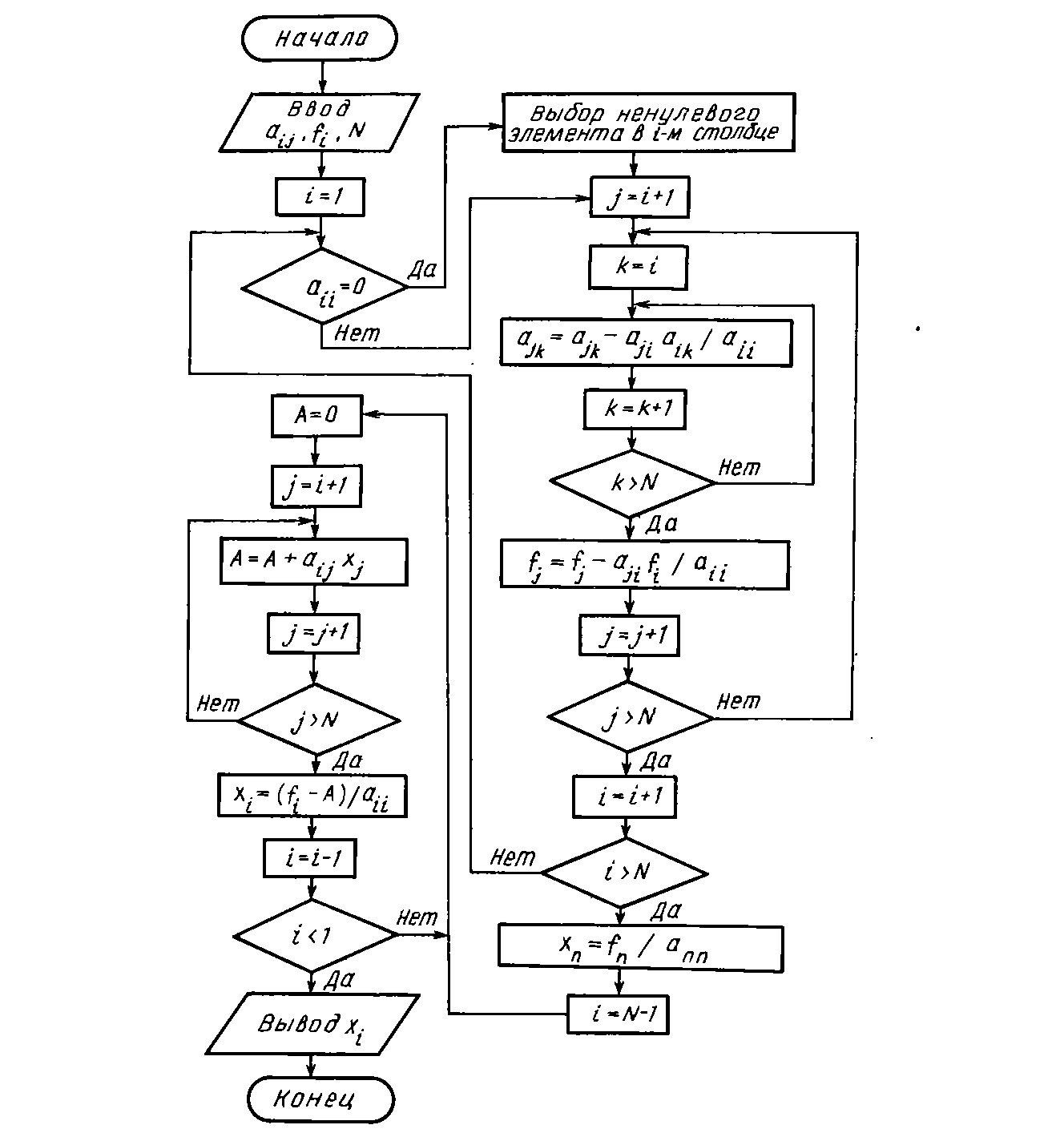
4 код программы

Программа разработана на языке Turbo Pascal в компьютерной среде Pascal ABC. Код программы представлен в приложении А.

5 Контрольный пример для отладки

Приведем пример решения СЛАУ :

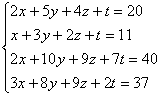
Решение.

Запишем матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

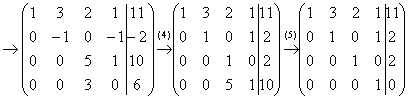
Выполненные преобразования: (1) Первую и вторую строки поменяли местами. (2) Ко второй строке прибавили первую строку, умноженную на –2.  К третьей строке прибавили первую строку, умноженную на –2. К четвертой строке прибавили первую строку, умноженную на –3. (3) К третьей строке прибавили вторую, умноженную на 4. К четвертой строке прибавили вторую, умноженную на –1. (4) У второй строки сменили знак. Четвертую строку разделили на 3 и поместили вместо третьей строки. (5) К четвертой строке прибавили третью строку, умноженную на  –5.

Обратный ход:

Ответ:

Решение системы в моей программе:

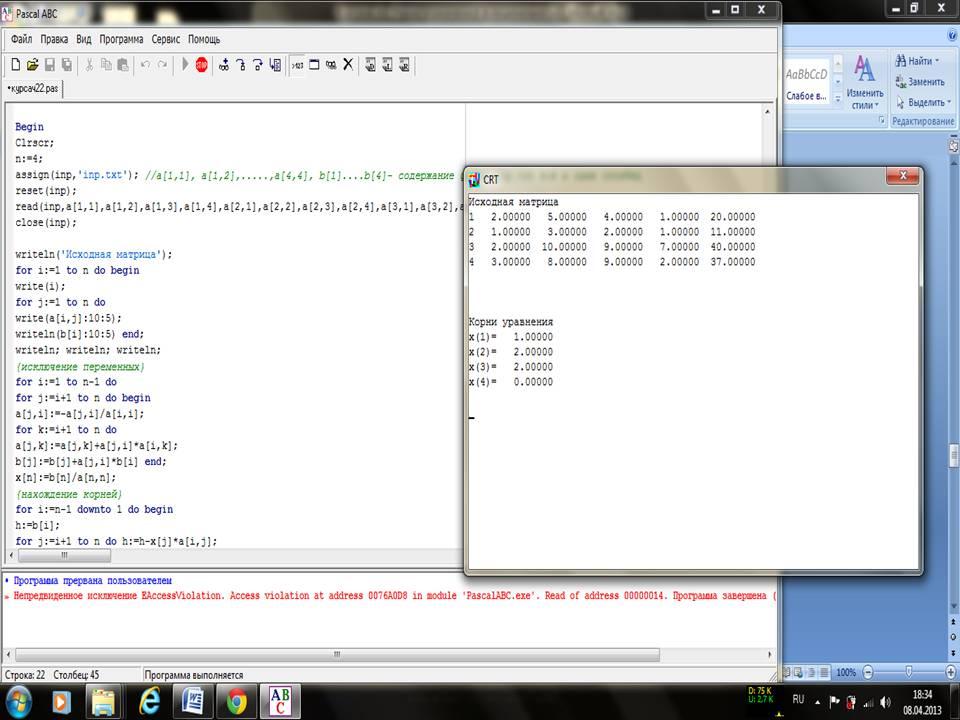
Спавнение: Вычисления вручную дают 4 корня уравнения равные: 0; 2; 2; 1. Компьютерная программа при решении тойже системы дает анологичные результаты. В этом вы можете убедиться взглянув на скриншот работы программы представленный выше. Следовательно программа работает правильно, проверенна на конкретном примере.

6 Описание программы

//Описание переменных, функций, процедур. Ссылка на приложение (код программы)

7 Инструкция

Пользоваться программой не так уж и сложно. Сначала до зауска среды Pascal ABC ,в которой будет исполненна программа, нужно в корневую папку с приложением PABCWork вставить текстовый файл inp. В этом файле нужно записать в столбик по порядку данные исходной матрицы, начиная с первого коэффициента и заканчивая кофициэнтом b4. Потом достаточно найти Программу и запустить ее, нажав на зеленный треугольник. И все, программа выведет окно с результатами счета.

8 Заключение.

В данной работе полностью разобрам метод Гаусса для систем линейных алгебраических уравнений. Помимо аналитического решения СЛАУ, метод Гаусса также применяется для нахождения матрицы, обратной к данной, определения ранга матрицы, численного решения СЛАУ в вычислительной технике.

Создана функциональная модель решения системы линейных алгебраических уравнений методом Гаусса. Записсана программа в среде Pascal ABC для реализации данной функциональной модели. Разобран конкретный пример решения СЛАУ и программа проверенна на данном примере.

9 Список использованной литературы:

Приложение А

Код программы.

uses crt;

 

type vec=array[1..4] of real;

mas=array[1..4,1..4] of real;

 

var a:mas; b,x:vec;

h,s:real;

i,j,k,n:integer;

inp:text;

 

Begin

Clrscr;

n:=4;

assign(inp,'inp.txt');

reset(inp);

read(inp,a[1,1],a[1,2],a[1,3],a[1,4],a[2,1],a[2,2],a[2,3],a[2,4],a[3,1],a[3,2],a[3,3],a[3,4],a[4,1],a[4,2],a[4,3],a[4,4], b[1],b[2],b[3],b[4]);

close(inp);

 

writeln('Исходная матрица');

for i:=1 to n do begin

write(i);

for j:=1 to n do

write(a[i,j]:10:5);

writeln(b[i]:10:5) end;

writeln; writeln; writeln;

{исключение переменных}

for i:=1 to n-1 do

for j:=i+1 to n do begin

a[j,i]:=-a[j,i]/a[i,i];

for k:=i+1 to n do

a[j,k]:=a[j,k]+a[j,i]*a[i,k];

b[j]:=b[j]+a[j,i]*b[i] end;

x[n]:=b[n]/a[n,n];

{нахождение корней}

for i:=n-1 downto 1 do begin

h:=b[i];

for j:=i+1 to n do h:=h-x[j]*a[i,j];

x[i]:=h/a[i,i]; end;

writeln('Корни уравнения');

for i:=1 to n do writeln('x(',i,')=',x[i]:10:5);

writeln;

readkey